LeetCode 栈&队列
20. 有效的括号
Given a string containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.
An input string is valid if:
- Open brackets must be closed by the same type of brackets.
- Open brackets must be closed in the correct order.
Note that an empty string is also considered valid.
Example 1:
Input: "()"
Output: true
Example 2:
Input: "()[]{}"
Output: true
Example 3:
Input: "(]"
Output: false
Example 4:
Input: "([)]"
Output: false
Example 5:
Input: "{[]}"
Output: true
解法一
这道题只要学过数据结构的肯定会做,典型的利用栈的题
public boolean isValid2(String s) {
if(s.length()<=0){
return true;
}
Stack<Character> stack=new Stack();
for(int i=0;i<s.length();i++){
if(s.charAt(i)=='(' || s.charAt(i)=='{' || s.charAt(i)=='['){
stack.push(s.charAt(i));
}else{
//注意这种情况,一开始就是])}
if(stack.isEmpty()){
return false;
}
char p=s.charAt(i);
if( (p==')' && stack.pop()!='(') || (p==']' && stack.pop()!='[') || (p=='}' && stack.pop()!='{')){
return false;
}
}
}
return stack.isEmpty();
}
解法二
其实和上面的解法是一样的,只不过是用的 stack 是自己用数组简单封装的栈
public class MyStack<T>{
T [] objValues=null;
int top=-1;
public MyStack(int size){
objValues= (T[]) new Object[size];
}
public void push(T obj){
objValues[++top]=obj;
}
public T peek(){
if (top<0) {
throw new RuntimeException("stack is isEmpty");
}
return objValues[top];
}
public T pop(){
if (top<0) {
throw new RuntimeException("stack is isEmpty");
}
//覆盖
return objValues[top--];
}
public boolean isEmpty(){
return top<0;
}
}
3ms,94%,比之前快了一点,去看了下 Stack 的源码,它的 pop 是真的删除,我的只是移动了指针,所以效率会高很多
后面的题可能还会利用这个
MyStack
解法三
今天看面筋看到一个写这道题,要求 O(1) 的空间复杂度
public boolean isValid(String s) {
if(s.length()<=0){
return true;
}
while(true){
int len=s.length();
s=s.replace("{}","");
s=s.replace("()","");
s=s.replace("[]","");
if (len==s.length()) {
break;
}
}
return "".equals(s);
}
100ms,效率感人,感觉应该说的是这种做法吧,当然还可以写正则表达式来匹配,但是我不太会写。
678. 有效的括号字符串
给定一个只包含三种字符的字符串:( ,) 和 *,写一个函数来检验这个字符串是否为有效字符串。有效字符串具有如下规则:
- 任何左括号
(必须有相应的右括号)。 - 任何右括号
)必须有相应的左括号(。 - 左括号
(必须在对应的右括号之前)。 *可以被视为单个右括号),或单个左括号(,或一个空字符串。- 一个空字符串也被视为有效字符串。
示例 1:
输入:"()"
输出:True
示例 2:
输入:"(*)"
输出:True
示例 3:
输入:"(*))"
输出:True
注意:
- 字符串大小将在 [1,100] 范围内。
解法一
看面筋看到的这一题,还是挺有意思的,评论区有人说了双栈,然后今天来试了下
public boolean checkValidString(String s) {
Stack<Integer> bracketStack=new Stack<>();
Stack<Integer> starStack=new Stack<>();
for (int i=0;i<s.length();i++) {
if (s.charAt(i)=='(') {
bracketStack.push(i);
}else if(s.charAt(i)=='*'){
starStack.push(i);
}else{
if (bracketStack.isEmpty()) {
if (starStack.isEmpty()) {
return false;
}
starStack.pop();
}else{
bracketStack.pop();
}
}
}
//消除左括号
while(!starStack.isEmpty() && !bracketStack.isEmpty()){
if(starStack.peek()>bracketStack.peek()){ //这里的逻辑不太好,其实可以很简单
bracketStack.pop();
}
starStack.pop();
}
return bracketStack.isEmpty();
}
很可惜没有bugfree,最后对左括号的判断改了好几次,一开始写的bracketStack.size()<=starStack().size() 然后提交后才意识到还要 "*(" 这样的情况,然后要消除这种情况也简单,一开始我再栈中存的就是 index,从 star 栈里面取比 bracket 栈 index 大的,然后消除,最后再看括号栈是不是空
//2020.4.10 重写一下
public boolean checkValidString(String s) {
Deque<Integer> stack=new ArrayDeque<>();
Deque<Integer> helpStack=new ArrayDeque<>();
for(int i=0;i<s.length();i++){
if(s.charAt(i)=='('){
stack.push(i);
}else if(s.charAt(i)==')'){
if(!stack.isEmpty()){
stack.pop();
}else{
if(helpStack.isEmpty()){
return false;
}
helpStack.pop();
}
}else{
helpStack.push(i);
}
}
while(!stack.isEmpty() && !helpStack.isEmpty()){
if(stack.pop()>helpStack.pop()){
return false;
}
}
return stack.isEmpty();
}
921. 使括号有效的最少添加
给定一个由 '(' 和 ')' 括号组成的字符串 S,我们需要添加最少的括号( '(' 或是 ')',可以在任何位置),以使得到的括号字符串有效。
从形式上讲,只有满足下面几点之一,括号字符串才是有效的:
- 它是一个空字符串,或者
- 它可以被写成
AB(A与B连接), 其中A和B都是有效字符串,或者 - 它可以被写作
(A),其中A是有效字符串。
给定一个括号字符串,返回为使结果字符串有效而必须添加的最少括号数。
示例 1:
输入:"())"
输出:1
示例 2:
输入:"((("
输出:3
示例 3:
输入:"()"
输出:0
示例 4:
输入:"()))(("
输出:4
提示:
S.length <= 1000S只包含'('和')'字符。
解法一
没啥好说的,easy 题
public int minAddToMakeValid(String S) {
int left=0,right=0;
int wa=0;
for(int i=0;i<S.length();i++){
if(S.charAt(i)=='('){
left++;
}else{
if(left>0){
left--;
}else{
wa++;
}
}
}
return wa+left;
}
394. 字符串解码
给定一个经过编码的字符串,返回它解码后的字符串。
编码规则为:k[encoded_string],表示其中方括号内部的 encoded_string 正好重复 k 次。注意 k 保证为正整数。
你可以认为输入字符串总是有效的;输入字符串中没有额外的空格,且输入的方括号总是符合格式要求的。
此外,你可以认为原始数据不包含数字,所有的数字只表示重复的次数 k ,例如不会出现像 3a 或 2[4] 的输入。
示例:
s = "3[a]2[bc]", 返回 "aaabcbc".
s = "3[a2[c]]", 返回 "accaccacc".
s = "2[abc]3[cd]ef", 返回 "abcabccdcdcdef".
解法一
借助栈直接在原字符上做改动
public String decodeString(String s) {
if (s==null || s.length()<=0) {
return "";
}
//转换为 StringBuilder 比较好处理,且效率较高
StringBuilder sb=new StringBuilder(s);
Stack<Integer> stack=new Stack<>();
int i=0;//遍历索引
while(i<sb.length()) {
if (sb.charAt(i)=='[') {
stack.push(i);
}else if(sb.charAt(i)==']'){
int left=stack.pop();//对应左括号索引
String temp=sb.substring(left+1,i);//相邻括号中的字符
int preInt=left;
//'['前的数字,一开始以为只是个位数,还是挺麻烦的
while(preInt-1>=0 && sb.charAt(preInt-1)>='0' && sb.charAt(preInt-1) <='9'){
preInt--;
}
//repeat 次数
int repeat=Integer.valueOf(sb.substring(preInt,left));
//删除 k[encoded_string]
sb.delete(preInt,Math.min(i+1,sb.length()));
for (int j=0;j<repeat;j++) {
//从 k 位置重新插入字符
sb.insert(preInt,temp);
}
//重新定位索引到尾部
i=preInt+(repeat*temp.length())-1;
}
i++;
}
return sb.toString();
}
一开始是想用一个额外的 String 来保存结果,结果发现比较麻烦,索性直接将原字符转换为 StringBuilder,然后借助 api 直接在原字符上做改动,因为是在原字符上做改动,所以索引的变化需要额外的注意,这也是最麻烦的一点,需要停下来稍微思考下才能确定,其他的还好,正常的思路,最初 WA 了一发是因为忽略了前面的数字可能是多位数😂
解法二
递归的方式,改成StringBuilder应该会好一点😂
private int index=0; //字符索引下标
public String decodeString(String s) {
if (s==null || s.length()<=0) {
return "";
}
String sb="";
while(index<s.length()){
if (s.charAt(index)==']') { //遇到右括号就结束
index++;//index 定位到右括号下一个
return sb;
}else if(s.charAt(index)>='0' && s.charAt(index)<='9'){
int temp=index;
while(index<s.length() && s.charAt(index)!='['){
index++;
}
int repeat=Integer.valueOf(s.substring(temp,index));
index++;//跳过'['
String rs=decodeString(s);//从左括号开始
for (int i=0;i<repeat;i++) {
sb+=rs;
}
}else{
sb+=s.charAt(index++);
}
}
return sb;
}
344. 反转字符串
编写一个函数,其作用是将输入的字符串反转过来。输入字符串以字符数组 char[] 的形式给出。
不要给另外的数组分配额外的空间,你必须原地修改输入数组、使用 O(1) 的额外空间解决这一问题。
你可以假设数组中的所有字符都是 ASCII 码表中的可打印字符。
示例 1:
输入:["h","e","l","l","o"]
输出:["o","l","l","e","h"]
示例 2:
输入:["H","a","n","n","a","h"]
输出:["h","a","n","n","a","H"]
解法一
很久之前做的了,本来是想单独搞一个递归专题,感觉没啥必要就直接加到一起了
public void reverseString(char[] s) {
if(s==null||s.length<=1)return;
reverseString(s,0,s.length-1);
}
public void reverseString(char[] s,int l,int r) {
if(l>=r){
return;
}
char temp=s[l];
s[l]=s[r];
s[r]=temp;
reverseString(s,++l,--r);
}
150. 逆波兰表达式求值
根据 逆波兰表示法,求表达式的值。
有效的运算符包括 +, -, *, / 。每个运算对象可以是整数,也可以是另一个逆波兰表达式
说明:
- 整数除法只保留整数部分。
- 给定逆波兰表达式总是有效的。换句话说,表达式总会得出有效数值且不存在除数为 0 的情况。
示例 1:
输入:["2", "1", "+", "3", "*"]
输出:9
解释:((2 + 1) * 3) = 9
示例 2:
输入:["4", "13", "5", "/", "+"]
输出:6
解释:(4 + (13 / 5)) = 6
示例 3:
输入:["10", "6", "9", "3", "+", "-11", "*", "/", "*", "17", "+", "5", "+"]
输出:22
解释:
((10 * (6 / ((9 + 3) * -11))) + 17) + 5
= ((10 * (6 / (12 * -11))) + 17) + 5
= ((10 * (6 / -132)) + 17) + 5
= ((10 * 0) + 17) + 5
= (0 + 17) + 5
= 17 + 5
= 22
解法一
public static int evalRPN(String[] tokens) {
//上面自己封装的 Stack
MyStack<Integer> stack=new MyStack<>(tokens.length);
for (int i=0;i<tokens.length;i++) {
if("+".equals(tokens[i])){
stack.push(stack.pop()+stack.pop());
} else if("-".equals(tokens[i])){
int rd1=stack.pop();
int rd2=stack.pop();
stack.push(rd2-rd1);
}else if("*".equals(tokens[i])){
stack.push(stack.pop()*stack.pop());
}else if("/".equals(tokens[i])){
int div1=stack.pop();
int div2=stack.pop();
stack.push(div2/div1);
}else{
stack.push(Integer.valueOf(tokens[i]));
}
}
return stack.peek();
}
12ms,90%,其实一开始看到这个题我是拒绝的,我以为又是啥数学题,然后仔细看了下发现挺简单的,思路就是利用栈,每次遇到符号就 pop 两个出来进行运算,然后再入栈,值得注意的地方就是减法和除法的顺序
71. 简化路径
以 Unix 风格给出一个文件的绝对路径,你需要简化它。或者换句话说,将其转换为规范路径。
在 Unix 风格的文件系统中,一个点(.)表示当前目录本身;此外,两个点 (..) 表示将目录切换到上一级(指向父目录);两者都可以是复杂相对路径的组成部分。更多信息请参阅:Linux / Unix 中的绝对路径 vs 相对路径
请注意,返回的规范路径必须始终以斜杠 / 开头,并且两个目录名之间必须只有一个斜杠 /。最后一个目录名(如果存在)不能以 / 结尾。此外,规范路径必须是表示绝对路径的最短字符串
示例 1:
输入:"/home/"
输出:"/home"
解释:注意,最后一个目录名后面没有斜杠。
示例 2:
输入:"/../"
输出:"/"
解释:从根目录向上一级是不可行的,因为根是你可以到达的最高级。
示例 3:
输入:"/home//foo/"
输出:"/home/foo"
解释:在规范路径中,多个连续斜杠需要用一个斜杠替换。
示例 4:
输入:"/a/./b/../../c/"
输出:"/c"
示例 5:
输入:"/a/../../b/../c//.//"
输出:"/c"
示例 6:
输入:"/a//b////c/d//././/.."
输出:"/a/b/c"
解法一
public static String simplifyPath(String path) {
MyStack<String> stack=new MyStack<>(path.length());
StringBuilder str=new StringBuilder(path);
//这里划分出来有一部分是空的 ""
String[] s=path.split("/");
for (int i=0;i<s.length;i++) {
if (!stack.isEmpty() && s[i].equals("..")) {
//.. 回溯
stack.pop();
}else if (!".".equals(s[i]) && !"".equals(s[i]) && !s[i].equals("..") ) {
//普通的英文字符 abcd
stack.push(s[i]);
}
}
if (stack.isEmpty()) {
return "/";
}
StringBuilder res=new StringBuilder();
for (int i=0;i<stack.size(); i++) {
res.append("/"+stack.get(i));
}
return res.toString();
}
//自己封装的 stack
public class MyStack<T>{
T [] objValues=null;
int top=-1;
public MyStack(int size){
objValues= (T[]) new Object[size];
}
public void push(T obj){
objValues[++top]=obj;
}
public T peek(){
if (top<0) {
throw new RuntimeException("stack is isEmpty");
}
return objValues[top];
}
public T pop(){
if (top<0) {
throw new RuntimeException("stack is isEmpty");
}
//覆盖
return objValues[top--];
}
public T get(int index){
if (index>top || index < 0) {
throw new RuntimeException("index is wrong");
}
return objValues[index];
}
public boolean isEmpty(){
return top<0;
}
public int size(){
return top+1;
}
}
这题本来是很简单的,但是我钻到牛角尖去了,一直想着怎么在遍历过程中处理,写了一堆 ifelse。还是太菜了啊,其实直接按照"/" 划分 split 字符串然后处理那个数组就可以了
225. 用队列实现栈
Implement the following operations of a stack using queues.
- push(x) – Push element x onto stack.
- pop() – Removes the element on top of the stack.
- top() – Get the top element.
- empty() – Return whether the stack is empty.
Example:
MyStack stack = new MyStack();
stack.push(1);
stack.push(2);
stack.top(); // returns 2
stack.pop(); // returns 2
stack.empty(); // returns false
Notes:
- You must use only standard operations of a queue – which means only
push to back,peek/pop from front,size, andis emptyoperations are valid. - Depending on your language, queue may not be supported natively. You may simulate a queue by using a list or deque (double-ended queue), as long as you use only standard operations of a queue.
- You may assume that all operations are valid (for example, no pop or top operations will be called on an empty stack).
解法一
很经典的题
class MyStack {
private ArrayDeque<Integer> queue=null;
/** Initialize your data structure here. */
public MyStack() {
queue=new ArrayDeque();
}
/** Push element x onto stack. */
public void push(int x) {
queue.add(x);
int size=queue.size();
//除了新加入的元素,其他的元素都出队再入队,将新加入的元素推置队列头
while(size-- >1){
queue.add(queue.pop());
}
}
/** Removes the element on top of the stack and returns that element. */
public int pop() {
return queue.pop();
}
/** Get the top element. */
public int top() {
return queue.peek();
}
/** Returns whether the stack is empty. */
public boolean empty() {
return queue.isEmpty();
}
}
很巧妙的做法,将元素前 n-1 个出队后再重新入队,1 2 --> 2 1 直接将堆顶推置队列头 ,将每次新加入的元素都放置队列头而不是队尾,这样实际上就完成了逆序的操作
这样 push 压栈时间复杂度O(N) ,pop/peek 时间复杂度O(1)
解法二
适用于 push 频繁的 stack
public class MyStack{
//形式上 q1 是负责进栈 q2 负责出栈
private LinkedList inQueue=new LinkedList();
private LinkedList outQueue=new LinkedList();
private void add(Object obj){
inQueue.add(obj);
}
private Object pop(){
// q1 ----> q2 留一个
while(inQueue.size()>1){
outQueue.add(inQueue.poll());
}
//交换 q1,q2 的引用
LinkedList temp;
temp=inQueue;
inQueue=outQueue;
outQueue=temp;
return outQueue.poll();
}
private Object peek(){
//q1 --->q2 留一个,最后一个不 poll, 最后 poll
while(inQueue.size()>1){
outQueue.add(inQueue.poll());
if(inQueue.size()==1){
outQueue.add(inQueue.peek());
}
}
//交换 q1,q2 的引用
LinkedList temp;
temp=inQueue;
inQueue=outQueue;
outQueue=temp;
return outQueue.poll();
}
}
两个队列,push 压栈时间复杂度O(1),pop/push 出栈时间复杂度O(N) ,出栈的时候将一个队列的前 n-1 个元素全部加入到另一个队列中作为缓存,然后将最后一个元素出栈,最后别忘了交换两个队列的引用,不然 push 的时候就会出问题,要保证inQueue 一直是入栈的队列,其中存放着所有的元素
232. 用栈实现队列
Implement the following operations of a queue using stacks.
- push(x) – Push element x to the back of queue.
- pop() – Removes the element from in front of queue.
- peek() – Get the front element.
- empty() – Return whether the queue is empty.
Example:
MyQueue queue = new MyQueue();
queue.push(1);
queue.push(2);
queue.peek(); // returns 1
queue.pop(); // returns 1
queue.empty(); // returns false
Notes:
- You must use only standard operations of a stack – which means only
push to top,peek/pop from top,size, andis emptyoperations are valid. - Depending on your language, stack may not be supported natively. You may simulate a stack by using a list or deque (double-ended queue), as long as you use only standard operations of a stack.
- You may assume that all operations are valid (for example, no pop or peek operations will be called on an empty queue).
解法一
class MyQueue {
Stack<Integer> inStack=null;
Stack<Integer> outStack=null;
/** Initialize your data structure here. */
public Stack2Queue232() {
inStack=new Stack<>();
outStack=new Stack<>();
}
/** Push element x to the back of queue. */
public void push(int x) {
inStack.push(x);
}
/** Removes the element from in front of queue and returns that element. */
public int pop() {
s2s();
return outStack.pop();
}
/** Get the front element. */
public int peek() {
s2s();
return outStack.peek();
}
/** Returns whether the queue is empty. */
public boolean empty() {
return outStack.isEmpty() && inStack.isEmpty();
}
private void s2s(){
if (outStack.isEmpty()) {
while(!inStack.isEmpty()) {
outStack.push(inStack.pop());
}
}
}
}
很上面一题是姊妹题,需要注意的地方就是s2s的时候要确保 stack2 栈是空的才能 push
155. 最小栈
设计一个支持 push,pop,top 操作,并能在常数时间内检索到最小元素的栈。
-
push(x) – 将元素 x 推入栈中。
-
pop() – 删除栈顶的元素。
-
top() – 获取栈顶元素。
-
getMin() – 检索栈中的最小元素。
示例:
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.getMin(); --> 返回 -2.
解法一
利用辅助栈,同步的 push 和 pop
class MinStack {
/** initialize your data structure here. */
private Stack<Integer> stack=null;
private Stack<Integer> helpStack=null;
public MinStack() {
stack=new Stack<>();
helpStack=new Stack<>();
}
public void push(int x) {
stack.push(x);
if (helpStack.isEmpty()) {
helpStack.push(x);
}else{
if (helpStack.peek()>x) {
helpStack.push(x);
}else{
helpStack.push(helpStack.peek());
}
}
}
public void pop() {
stack.pop();
helpStack.pop();
}
public int top() {
return stack.peek();
}
public int getMin() {
return helpStack.peek();
}
}
解法二
在上面的基础上进行空间的优化
class MinStack {
/** initialize your data structure here. */
private Stack<Integer> stack=null;
private Stack<Integer> helpStack=null;
public MinStack() {
stack=new Stack<>();
helpStack=new Stack<>();
}
public void push(int x) {
stack.push(x);
if (helpStack.isEmpty()) {
helpStack.push(x);
}else if (x<=helpStack.peek()) {
//相等的也要入栈,不然不好控制后面出栈
helpStack.push(x);
}
}
public void pop() {
int top=stack.pop();
//和辅助栈栈顶相同就出栈
if(top==helpStack.peek()){
helpStack.pop();
}
/*
if(stack.pop()==helpStack.peek()){
helpStack.pop();
}*/
}
public int top() {
return stack.peek();
}
public int getMin() {
return helpStack.peek();
}
}
其实这里有一个地方把我卡了一会儿,就是出栈的时候,我开始为了简洁 if 的条件写的
stack.pop()==helpStack.peek() 然后卡在了一个 case 上,想了半天才意识到是Integer的问题,这里弹出来的是两个Integer并不会自动拆箱,而且值是不在 -128~127 之间的,所以就 false 了
解法三
帅地上看见的解法,在栈中存一个 diff 差值,代表当前元素和入栈前的 min 的差值,空间复杂度为 O(1),但是这种做法限制比较多,比如数据的大小会有限制,同时貌似也无法做peek()操作
public class MinStack155_2{
/** initialize your data structure here. */
private Stack<Integer> stack=null;
private int min=0;
public MinStack155_2() {
stack=new Stack<>();
}
public void push(int x) {
if (stack.isEmpty()) {
min=x;
stack.push(0);
}else{
int diff=x-min;
min=diff>0?min:x;
stack.push(diff);
}
}
public void pop() {
int diff=stack.pop();
//小于等于 0 说明 min 就是当前真实的栈顶元素,也就是说 min-minPre=diff
min=diff<=0?min-diff:min;
}
/*public int top() {
int diff=stack.peek();
return diff<=0?min:diff-min;
}*/
public int getMin() {
return min;
}
}
779. 第 K 个语法符号
On the first row, we write a 0. Now in every subsequent row, we look at the previous row and replace each occurrence of 0 with 01, and each occurrence of 1 with 10.
Given row N and index K, return the K-th indexed symbol in row N. (The values of K are 1-indexed.) (1 indexed).
Examples:
Input: N = 1, K = 1
Output: 0
Input: N = 2, K = 1
Output: 0
Input: N = 2, K = 2
Output: 1
Input: N = 4, K = 5
Output: 1
Explanation:
row 1: 0
row 2: 01
row 3: 0110
row 4: 01101001
Note:
Nwill be an integer in the range[1, 30].Kwill be an integer in the range[1, 2^(N-1)].
解法一
找规律,前半部分和后半部分是有一定规律的,把前六行都写出来
第一行:0
第二行:01
第三行:01|10
第四行:01 10|10 01
第五行:01 10 10 01|10 01 01 10
第六行:01 10 10 01 10 01 01 10 | 10 01 01 10 01 10 10 01
N%2!=0 对称,第 K 个等于 2^(N-1)-K+1 N%2==0 互补对称
public int kthGrammar(int N, int K) {
if(K==1 || N==1){
return 0;
}
if(K==2){
return 1;
}
int len=1<<(N-1); //当前行长度
if(K>len/2){ //大于 1/2
//结合上面的规律,找前半部分和自己等价的位置
if(N%2!=0){
K=len-K+1;
}else{
if(K%2==0){
K=len-K+2;
}else{
K=len-K;
}
}
}
//去上一行继续
return kthGrammar(N-1,K);
}
时间复杂第 O(N),思路还算清晰,最开始没想到用位运算来算长度,用的pow()最后效率差不多,可能是底层做了优化。
解法二
这种解法实际上就是把整个序列看作一颗满二叉树,每个节点的值和父节点其实是有对应关系的,如果 K 是偶数那么就和父节点的值相反,否则就相同,所以我们可以递归的去找父节点对应的 index 的值。
//01 排列
// 0
// / \
// 0 1
// / \ / \
// 0 1 1 0
// / \ / \ / \ / \
//0 1 1 0 1 0 0 1
public int kthGrammar(int N, int K) {
if (K==1) return 0;
//(K+1)/2 是对应父节点的 index
int parent=kthGrammar(N-1,(K+1)/2);
//取反
int f_parent=-(parent-1);
if (K%2==0) {
return f_parent;
}
return parent;
}
时间复杂度依然是O(N) 但是比上面那种要更清晰明了
解法三
这个解法其实和上面的思路是一样的,都是利用父节点和 K 的奇偶来判断,其实仔细看上面的代码你会发现 N 其实并没有实际的意义,具体 K 的值只和 K 本身有关,下面的解法就没有用到 N.
public static int kthGrammar3(int N, int K) {
boolean r=false;
while(K>1){
if (K%2==0) {
K=K/2;
r=!r;
}else{
K=(K+1)/2;
}
}
return r?1:0;
}
这题其实还有一种解法,利用二进制,对 K 做奇偶检验,貌似时间复杂度是 O(1)。
50. Pow(x, n)
实现 pow(x, n) ,即计算 x 的 n 次幂函数。
解法一
这里就要介绍一种快速幂算法了
public static double fastPow(double x,int n){
if(n==0){
return 1;
}
if(n<0){
x=1/x;
n=-n;
}
double res=fastPow(x,n/2);
if(n%2==0){
return res*res;
}
return res*res*x;
}
核心思想就是 x^n=(x^2/n)^2,常规累乘的方式计算时间复杂度是 O(N) 因为要遍历所有的元素,但是其实知道了x^n/2之后 x^n就可以直接平方得到了不用继续遍历,整体时间复杂度为 O(logN)
2019.8.20,又写了一遍,提交然后没过。看了下给的测试用例,最后一个给的 n 是 -2^31 也就是 int 整数的最小值,int 类型的取值范围是 -2^31 ~ 2^31-1 而这个负值在这里取反之后会直接溢出最后得到的还是 -2^31 ,所以这里这样写 if 会执行两次,x 就又会变回来,所以结果直接就是Infinity无穷大了,所以为了保证 if 只会执行一次可以将其封装一下
public static double myPow(double x, int n) {
if(n<0){
x=1/x;
n=-n;
}
return fastPow(x,n);
}
public static double fastPow(double x,int n){
if(n==0){
return 1.0;
}
double half=fastPow(x,n/2);
if(n%2==0)
return half*half;
return half*half*x;
}
5222. 分割平衡字符串
在一个「平衡字符串」中,‘L’ 和 ‘R’ 字符的数量是相同的。
给出一个平衡字符串 s,请你将它分割成尽可能多的平衡字符串。
返回可以通过分割得到的平衡字符串的最大数量
示例 1:
输入:s = "RLRRLLRLRL"
输出:4
解释:s 可以分割为 "RL", "RRLL", "RL", "RL", 每个子字符串中都包含相同数量的 'L' 和 'R'。
示例 2:
输入:s = "RLLLLRRRLR"
输出:3
解释:s 可以分割为 "RL", "LLLRRR", "LR", 每个子字符串中都包含相同数量的 'L' 和 'R'。
示例 3:
输入:s = "LLLLRRRR"
输出:1
解释:s 只能保持原样 "LLLLRRRR".
提示:
1 <= s.length <= 1000s[i] = 'L' 或 'R'
解法一
19.10.13 的周赛的第 1 题,果然比赛和刷题还是不一样,差点没做出来。
public static int balancedStringSplit(String s) {
if (s.length()%2==1) {
return 0;
}
Stack<Character> stack=new Stack<>();
int count=0;
for(int i=0;i<s.length();i++){
if (!stack.isEmpty() ){
if(s.charAt(i)==stack.peek()) {
stack.push(s.charAt(i));
}else{
stack.pop();
if (stack.isEmpty()) {
count++;
}
}
}else{
stack.push(s.charAt(i));
}
}
return count;
}
1249. 移除无效的括号
给你一个由 ‘(’、’)’ 和小写字母组成的字符串 s。
你需要从字符串中删除最少数目的 ‘(’ 或者 ‘)’ (可以删除任意位置的括号),使得剩下的「括号字符串」有效。
请返回任意一个合法字符串。
有效「括号字符串」应当符合以下 任意一条 要求:
- 空字符串或只包含小写字母的字符串
- 可以被写作 AB(A 连接 B)的字符串,其中 A 和 B 都是有效「括号字符串」
- 可以被写作 (A) 的字符串,其中 A 是一个有效的「括号字符串」
示例 1:
输入:s = "lee(t(c)o)de)"
输出:"lee(t(c)o)de"
解释:"lee(t(co)de)" , "lee(t(c)ode)" 也是一个可行答案。
示例 2:
输入:s = "a)b(c)d"
输出:"ab(c)d"
示例 3:
输入:s = "))(("
输出:""
解释:空字符串也是有效的
示例 4:
输入:s = "(a(b(c)d)"
输出:"a(b(c)d)"
提示:
1 <= s.length <= 10^5s[i]可能是'('、')'或英文小写字母
解法一
11.3 周赛第三题,这题倒是没什么障碍,用栈就 ok,不过我这里实现的不太好,replace 时间复杂度略高,应该用一个数组做 mark 最后用 StringBuilder 做 append 应该效率会高很多
public String minRemoveToMakeValid(String s) {
StringBuilder sb=new StringBuilder(s);
Stack<Integer> stack=new Stack<>();
for (int i=0;i<s.length();i++) {
if (s.charAt(i)>='a' && s.charAt(i)<='z') {
continue;
}
if (s.charAt(i)==')') {
if (stack.isEmpty()) {
sb.replace(i,i+1,"*");
}else{
stack.pop();
}
}
if (s.charAt(i)=='(') {
stack.push(i);
}
}
while (!stack.isEmpty()) {
int temp=stack.pop();
sb.replace(temp,temp+1,"*");
}
String res=sb.toString().replace("*","");
return res;
}
856. 括号的分数
给定一个平衡括号字符串 S,按下述规则计算该字符串的分数:
- () 得 1 分。
- AB 得 A + B 分,其中 A 和 B 是平衡括号字符串。
- (A) 得 2 * A 分,其中 A 是平衡括号字符串。
示例 1:
输入: "()"
输出: 1
示例 2:
输入: "(())"
输出: 2
示例 3:
输入: "()()"
输出: 2
示例 4:
输入: "(()(()))"
输出: 6
提示:
- S 是平衡括号字符串,且只含有 ( 和 ) 。
- 2 <= S.length <= 50
解法一
public int scoreOfParentheses(String S) {
Stack<Integer> stack=new Stack<>();
for(int i=0;i<S.length();i++){
if(S.charAt(i)=='('){
stack.push(-11111);
}else{
//遇到右括号,下面的分支都是处理 ")"
int top=stack.peek();
if(top == -11111){ //栈顶是左括号,将 ( --> 1
stack.pop();
stack.push(1);
}else{
int sum=0; //遇到数值了
while(!stack.isEmpty()){
int temp=stack.pop();
//弹出去,直到遇到 "("就* 2, 其实就是把"(1"-->2
if(temp==-11111){
sum*=2;
break;
}
sum+=temp;
}
stack.push(sum);
}
}
}
int res=0;
while(!stack.isEmpty()) res+=stack.pop();
return res;
}
这种解法一开始也没想出来,其实这种就类似于消消乐游戏一样,就按照题目的逻辑来写,从左向右,栈中存标识左括号的数值,这里我用的-11111 表示( ,然后向右移动,一边移动一边将()给消除掉,其实上面的逻辑自己走一边就通了
解法二
这个解法就带有点技巧性了,看懂上面的注释,下面的代码就很简单了
// (()(())) = 2*()+2*(())= (())+((()))
public int scoreOfParentheses(String S) {
int k=0,res=1;
for (int i=0;i<S.length();i++) {
if (S.charAt(i)=='(') {
k++; //k 用来计算括号的深度
}else{
k--;
if (S.charAt(i-1)=='(') {
//"()"闭合的时候计算一波
res+= 1<<k; //2^k
}
}
}
return res;
}
946. 验证栈序列
给定 pushed 和 popped 两个序列,每个序列中的 值都不重复,只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时,返回 true 否则,返回 false
示例 1:
输入:pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
输出:true
解释:我们可以按以下顺序执行:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
示例 2:
输入:pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
输出:false
解释:1 不能在 2 之前弹出。
提示:
0 <= pushed.length == popped.length <= 10000 <= pushed[i], popped[i] < 1000pushed是popped的排列
解法一
直接用栈模拟,可惜没有 bugfree…
public boolean validateStackSequences(int[] pushed, int[] popped) {
if(pushed==null || pushed.length<=0) return true;
Deque<Integer> stack=new ArrayDeque<>();
int popIndex=0;
int pushIndex=0;
//pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
//[1,2,3,4,5] [4,3,5,1,2]
//[1,0] [1,0]
while(pushIndex<pushed.length){
stack.push(pushed[pushIndex++]);
while(!stack.isEmpty()&&popped[popIndex]==stack.peek()){
stack.pop();
popIndex++;
}
}
return stack.isEmpty();
}
每进一个元素就判断栈顶和出栈顺序的头是否相等,然后出栈,最后看栈中是否为空就 ok
NC560. 打字
牛妹在练习打字,现在按照时间顺序给出牛妹按下的键(以字符串形式给出,’<‘代表回退 backspace,其余字符均是牛妹打的字符,字符只包含小写字母与’<’),牛妹想知道最后在屏幕上显示的文本内容是什么。 在文本内容为空的时候也可以按回退 backspace(在这种情况下没有任何效果)。 示例 1
输入:"acv<"
输出:"ac"
说明:
牛妹在打完"acv"之后按了回退,所以最后是"ac"
解法一
也可以直接数组模拟
public String Typing (String s) {
// write code here
Deque<Integer> stack = new ArrayDeque<>();
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '<') {
if (stack.isEmpty()) {
continue;
}
stack.pop();
}else{
stack.push(i);
}
}
StringBuilder sb = new StringBuilder();
while(!stack.isEmpty()){
sb.append(s.charAt(stack.pop()));
}
return sb.reverse().toString();
}
BFS 广搜
279. 完全平方数
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4.
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9.
解法一
这题在上一篇 dp 专题 中有讲过,不过是 dp 的解法,这里主要记录 BFS 的解法
public static int numSquares2(int n) {
Queue<Pair> queue=new LinkedList<>();
boolean[] visit=new boolean[n+1];
queue.add(new Pair(n,0));
visit[n]=true;
while(!queue.isEmpty()){
Pair pair=queue.poll();
int num=pair.num;
int step=pair.step;
//nums=0 说明找到了,并且一定是最短的
if (num==0) {
return step;
}
for (int i=1;i*i<=num;i++) {
int temp=num-i*i;
//注意不要添加重复的元素
if (!visit[temp]) {
queue.add(new Pair(temp,step+1));
visit[temp]=true;
}
}
}
return -1;
}
static class Pair{
public int step;
public int num;
public Pair(int num,int step){
this.num=num;
this.step=step;
}
}
30ms 90%,比 dp 的方式会快很多,思路就是将这个问题转换为求图的最短路径的问题,找到一个最短的从 n 到 0 的以平方数为差的路径
127. 单词接龙
Given two words (beginWord and endWord), and a dictionary’s word list, find the length of shortest transformation sequence from beginWord to endWord, such that:
- Only one letter can be changed at a time.
- Each transformed word must exist in the word list. Note that beginWord is not a transformed word.
Note:
- Return 0 if there is no such transformation sequence.
- All words have the same length.
- All words contain only lowercase alphabetic characters.
- You may assume no duplicates in the word list.
- You may assume beginWord and endWord are non-empty and are not the same.
Example 1:
Input:
beginWord = "hit",
endWord = "cog",
wordList = ["hot","dot","dog","lot","log","cog"]
Output: 5
Explanation: As one shortest transformation is "hit" -> "hot" -> "dot" -> "dog" -> "cog",
return its length 5.
Example 2:
Input:
beginWord = "hit"
endWord = "cog"
wordList = ["hot","dot","dog","lot","log"]
Output: 0
Explanation: The endWord "cog" is not in wordList, therefore no possible transformation.
解法一
这题其实很久以前就写过了,当时是看了啊哈算法的一些 BFS 算法然后仿照书上的写的,书上是 C 语言写的,所以最后我写的时候也按照 C 的格式去写了😅,写的贼啰嗦,现在又用"Java"的方式又重新写了一遍
private static int[] mark;
int min = Integer.MAX_VALUE;
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
// 不存在
mark = new int[wordList.size() + 1];
if (!wordList.contains(endWord)) {
return 0;
}
// BFS
int head = 0, tail = 0;
// 初始化队列
Que[] que = new Que[wordList.size() + 1];
// 循环促使话述祖
for (int i = 0; i < que.length; i++) {
que[i] = new Que();
}
que[tail].word = beginWord;
que[tail].step = 1;
tail++;
int flag=0;
while (head < tail) {
// 遍历字典
for (int i = 0; i < wordList.size(); i++) {
if (mark[i] == 0 && cmp(wordList.get(i), que[head].word)) {
que[tail].word = wordList.get(i);
//这里是从 head 开始的,所以应该是 head 的步数+1
que[tail].step=que[head].step+1;
// 标记为已经走过
mark[i] = 1;
// 统计最小步数
if (que[tail].word.equals(endWord)) {
//跳出循环
flag=1;
break;
}
tail++;
}
}
if(flag==1){
break;
}
// 每次检查完一个单词就将其出队列
head++;
}
return que[tail].step;
}
// 写一个函数判段没吃是否只变化了一个字母
private boolean cmp(String s1, String s2) {
int count = 0;
for (int i = 0; i < s1.length(); i++) {
if (s1.charAt(i) != s2.charAt(i)) {
count++;
}
}
return count == 1;
}
// 内部类
class Que {
String word;
int step;
}
这就是当时写的解法,思路就是 BFS,只不过写的复杂了
解法二
public int ladderLength(String beginWord, String endWord, List<String> wordList) {
//visit 数组
boolean[] visit=new boolean[wordList.size()];
if (!wordList.contains(endWord)) {
return 0;
}
Queue<Pair> queue=new LinkedList<>();
queue.add(new Pair(beginWord,1));
//int flag=0;
while (!queue.isEmpty()) {
Pair pair=queue.poll();
// 统计最小步数,放在内循环中会快一点
/*if (pair.word.equals(endWord)) {
return pair.step;
}*/
// 遍历字典
for (int i = 0; i < wordList.size(); i++) {
if (!visit[i] && cmp(wordList.get(i),pair.word)) {
if (wordList.get(i).equals(endWord)) {
//这里加 1 是因为取的是 pair 的 step
//到当前这个单词还要多走一步
return pair.step+1;
}
queue.add(new Pair(wordList.get(i),pair.step+1));
//标记为已经走过
visit[i] = true;
}
}
}
return 0;
}
//是否只变化了一个字符
private boolean cmp(String s1, String s2) {
int count = 0;
for (int i = 0; i < s1.length(); i++) {
if (s1.charAt(i) != s2.charAt(i)) {
count++;
if (count>1) {
return false;
}
}
}
return count == 1;
}
//Pair
class Pair {
String word;
int step;
public Pair(String word,int step){
this.word=word;
this.step=step;
}
}
273ms,47%中规中矩的做法,连续写了好几题 BFS 的,总算是对 BFS 的板子有点熟悉了,这题还有两个可以优化的点 ① 双端 BFS ② 寻找下一个字符串的方式,只不过我没咋看懂,等看懂了再来补充,那种方式时间好像可以缩减到 20ms 内。….
这题有个困难版本,需要打印出所有的最短序列,这个在我很久之前的一篇文章中也有讲,但是至今我也还没有 AC,一直是 TLE,现在回头看我之前的代码已经看不懂了。写了 100 多行,略复杂 BFS+DFS 的做法,可能是没处理好所以 TLE 了,感兴趣可以看看 那篇文章
542. 01 矩阵
给定一个由 0 和 1 组成的矩阵,找出每个元素到最近的 0 的距离。
两个相邻元素间的距离为 1
示例 1: 输入:
0 0 0
0 1 0
0 0 0
输出:
0 0 0
0 1 0
0 0 0
示例 2: 输入:
0 0 0
0 1 0
1 1 1
输出:
0 0 0
0 1 0
1 2 1
注意:
- 给定矩阵的元素个数不超过 10000
- 给定矩阵中至少有一个元素是 0
- 矩阵中的元素只在四个方向上相邻:上、下、左、右
解法一
憨憨的 BFS 解法
//遍历每一个 1,BFS 寻找离他最近的 0, 一次只能确定一个 1, 效率略低
public int[][] updateMatrix(int[][] matrix) {
if (matrix == null || matrix.length <=0 || matrix[0].length <=0) {
return new int[][]{};
}
for (int i=0;i<matrix.length;i++) {
for (int j=0;j<matrix[0].length;j++) {
if (matrix[i][j] == 1) {
matrix[i][j]=findMinDis(matrix,i,j);
}
}
}
return matrix;
}
private int[][] direction={{1,0},{0,1},{-1,0},{0,-1}};
public int findMinDis(int[][] matrix,int x,int y){
Queue<Pair> queue=new LinkedList<>();
//boolean[][] visit=new boolean[matrix.length][matrix[0].length];
queue.add(new Pair(x,y,0));
//visit[x][y]=true;
while(!queue.isEmpty()){
Pair pair=queue.poll();
for (int i=0;i<direction.length;i++) {
int nx=pair.x + direction[i][0];
int ny=pair.y + direction[i][1];
if (isValid(matrix,nx,ny) /*&& !visit[nx][ny]*/) {
//visit[nx][ny]=true;
if (matrix[nx][ny] == 0) {
return pair.step+1;
}
queue.add(new Pair(nx,ny,pair.step+1));
}
}
}
return -1; //题目说了一定有 0, 所以不会走到这里
}
public boolean isValid(int[][] matrix,int x,int y){
return x>=0 && x<matrix.length && y>=0 && y<matrix[0].length;
}
class Pair{
int x;
int y;
int step;
public Pair(int x,int y,int step){
this.x=x;
this.y=y;
this.step=step;
}
}
可以看到代码中有很明显的改动痕迹,最开始是用 visit 数组保证每一个元素只会进队列一次,不会重复的进队列,但是这里为什么我去掉了呢?
其实主要是一开始提交的解法超时了,把 visit 数组去掉就过了,在数组过大的时候每次 BFS 都要开辟一个 matrix 大小的 boolean 数组,这无疑会极其耗费时间,但是为什么不加 visit 数组不会死循环呢?
确实,如果不加 visit 数组那么确实是有可能会导致死循环的,两个节点互相重复添加对方,但是这一题有个很关键的地方,题目说明了一定会有 0,也就是说一定会解,那么就不会死循环,举一个很简单的例子
【0,1,1】 这里我们先考虑中间的 1,然后我们按照下右上左的顺序去添加周围的节点,那么队列中就为末尾的[1] ,当遍历到右的时候发现是 0,直接 return,然后我们考虑下一个 1,转了一圈队列中只有一个中间的[1] , 然后我们又重复刚刚的步骤会将末尾的 1 又加入队列,但是下一次遍历就会找到最左边的 0,然后返回,所以并不会死循环,当然这样做的前提是一定要有解!
解法二
另一种更好的做法,以 0 作为源,向四周 BFS,同时更新周围的 1 的值
//update: 2020.4.15
private int[][] dir={{1,0},{0,1},{-1,0},{0,-1}};
public int[][] updateMatrix(int[][] matrix) {
if(matrix==null || matrix.length<=0) return matrix;
boolean[][] visit=new boolean[matrix.length][matrix[0].length];
Queue<Pair> queue=new LinkedList<>();
for(int i=0;i<matrix.length;i++){
for(int j=0;j<matrix[0].length;j++){
if(matrix[i][j]==0){
queue.add(new Pair(i,j,0));
visit[i][j]=true;
}else{
matrix[i][j]=Integer.MAX_VALUE;
}
}
}
while(!queue.isEmpty()){
Pair pair=queue.poll();
for(int i=0;i<dir.length;i++){
int nx=pair.x+dir[i][0];
int ny=pair.y+dir[i][1];
if(valid(matrix,nx,ny) && !visit[nx][ny]){
queue.add(new Pair(nx,ny,pair.step+1));
matrix[nx][ny]=pair.step+1; //这里不用判断是不是变小,第一次遇到的就是最近的
visit[nx][ny]=true;
}
}
}
return matrix;
}
public boolean valid(final int[][] matrix,int x,int y){
return x>=0 && x<matrix.length && y>=0 && y<matrix[0].length;
}
class Pair{
int x,y;
int step;
public Pair(int x,int y,int step){
this.x=x;
this.y=y;
this.step=step;
}
}
核心思想就是 把所有 1 都置为最大值,把所有为 0 的位置加入队列中,每次从队列中 poll 一个节点,更新其四周的节点,如果被更新的节点距离变小了就将其也加入队列准备更新其邻接点 step 是递增的,第一次遇到的一定是最近的
多源 BFS,参考下面的 994. 腐烂的橘子 和 1162. 地图分析
解法三
这题的最优解应该是动态规划的解法,我实在是懒得写(菜),其实和哪个 不同路径有点类似,每个 1 离他最近的 0 的距离其实就是它周围的元素离 0 最近的距离+1
也就是
matrix[i][j] =min(dp[i][j-1],dp[i-1][j],dp[i+1][j],dp[i][j+1]) + 1但是我们不可能同时求出是个方向的最小值,所以我们需要两次遍历,第一遍从左上到右下,第二遍从右下到左上,两次遍历就可以确定每个节点的值,代码以后有时间再来写
1306. 跳跃游戏 III
这里有一个非负整数数组 arr,你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时,你可以跳到 i + arr[i] 或者 i - arr[i]。
请你判断自己是否能够跳到对应元素值为 0 的 任意 下标处。
注意,不管是什么情况下,你都无法跳到数组之外
示例 1:
输入:arr = [4,2,3,0,3,1,2], start = 5
输出:true
解释:
到达值为 0 的下标 3 有以下可能方案:
下标 5 -> 下标 4 -> 下标 1 -> 下标 3
下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3
示例 2:
输入:arr = [4,2,3,0,3,1,2], start = 0
输出:true
解释:
到达值为 0 的下标 3 有以下可能方案:
下标 0 -> 下标 4 -> 下标 1 -> 下标 3
示例 3:
输入:arr = [3,0,2,1,2], start = 2
输出:false
解释:无法到达值为 0 的下标 1 处。
提示:
1 <= arr.length <= 5 * 10^40 <= arr[i] < arr.length0 <= start < arr.length
解法一
BFS,某次周赛的第 3 题,还是挺简单的,可惜那次没参加
public boolean canReach(int[] arr, int start) {
boolean[] visit=new boolean[arr.length];
Queue<Integer> queue=new LinkedList<>();
queue.add(start);
visit[start]=true;
while(!queue.isEmpty()){
int cur=queue.poll();
if (arr[cur] == 0) {
return true;
}
if (cur-arr[cur]>=0 && !visit[cur-arr[cur]]) {
queue.add(cur-arr[cur]);
visit[cur-arr[cur]]=true;
}
if (cur+arr[cur]<arr.length && !visit[cur+arr[cur]]) {
queue.add(cur+arr[cur]);
visit[cur+arr[cur]]=true;
}
}
return false;
}
解法二
DFS 解法,没啥好说的
public boolean canReach(int[] arr,int start){
boolean[] visit=new boolean[arr.length];
return dfs(arr,start,visit);
}
public boolean dfs(int[] arr,int index,boolean[] visit){
if (arr[index] == 0) {
return true;
}
visit[index]=true;
boolean b=false;
if (index-arr[index] >=0 && !visit[index-arr[index]]) {
b=dfs(arr,index-arr[index],visit);
}
if (index+arr[index] <arr.length && !visit[index+arr[index]]) {
return b|dfs(arr,index+arr[index],visit);
}
return b;
}
5314. 跳跃游戏 IV
给你一个整数数组 arr ,你一开始在数组的第一个元素处(下标为 0)。
每一步,你可以从下标 i 跳到下标:
- i + 1 满足:i + 1 < arr.length
- i - 1 满足:i - 1 >= 0
- j 满足:arr[i] == arr[j] 且 i != j
请你返回到达数组最后一个元素的下标处所需的 最少操作次数 。 注意:任何时候你都不能跳到数组外面。
示例 1:
输入:arr = [100,-23,-23,404,100,23,23,23,3,404]
输出:3
解释:那你需要跳跃 3 次,下标依次为 0 --> 4 --> 3 --> 9 。下标 9 为数组的最后一个元素的下标。
示例 2:
输入:arr = [7]
输出:0
解释:一开始就在最后一个元素处,所以你不需要跳跃。
示例 3:
输入:arr = [7,6,9,6,9,6,9,7]
输出:1
解释:你可以直接从下标 0 处跳到下标 7 处,也就是数组的最后一个元素处。
示例 4:
输入:arr = [6,1,9]
输出:2
示例 5:
输入:arr = [11,22,7,7,7,7,7,7,7,22,13]
输出:3
提示:
1 <= arr.length <= 5 * 10^4-10^8 <= arr[i] <= 10^8
解法一
19 双周赛的最后一题,讲道理挺简单的(可我还是 TLE 了好长时间)
public int minJumps(int[] arr) {
Queue<Pair> queue=new LinkedList<>();
boolean[] visit=new boolean[arr.length];
HashMap<Integer,List<Integer>> map=new HashMap<>();
//构建等值的索引 连续相同的只保留头尾
for (int i=0;i<arr.length;i++) {
List<Integer> lis=map.computeIfAbsent(arr[i],k->new ArrayList<>());
if (!((i-1>=0&&arr[i-1]==arr[i]) && (i+1<arr.length&&arr[i+1]==arr[i]))){
lis.add(i);
}
}
queue.add(new Pair(0,0));
visit[0]=true;
while(!queue.isEmpty()){
Pair pair=queue.poll();
if (pair.index==arr.length-1) {
return pair.step;
}
if(pair.index+1<arr.length && !visit[pair.index+1]){
queue.add(new Pair(pair.index+1,pair.step+1));
visit[pair.index+1]=true;
}
if (pair.index-1>=0 && !visit[pair.index-1]) {
queue.add(new Pair(pair.index-1,pair.step+1));
visit[pair.index-1]=true;
}
List<Integer> list=map.get(arr[pair.index]);
for (int i=list.size()-1;i>=0;i--) {
int idx=list.get(i);
if (!visit[idx]) {
queue.add(new Pair(idx,pair.step+1));
visit[idx]=true;
}
}
}
return -1;
}
class Pair{
int index;
int step;
public Pair(int index,int step){
this.index=index;
this.step=step;
}
}
看一下数据范围,直接 BFS 遍历跳同值的肯定不行,所以想到了用 map 预处理同值的索引,结果还是 TLE 了,后面一个 case 有 50000 个 7,这里即使做了 map 索引但是无奈太多了,依然会超时,这里其实这么多 7,只有头和尾的 7 是用的,其他位置的 7 都是无用的,可以直接忽略,所以构建索引的时候可以跳过这些中间位置,这样可以节省很多时间
690. 员工的重要性
给定一个保存员工信息的数据结构,它包含了员工唯一的 id,重要度 和 直系下属的 id。
比如,员工 1 是员工 2 的领导,员工 2 是员工 3 的领导。他们相应的重要度为 15, 10, 5。那么员工 1 的数据结构是 [1, 15, [2]],员工 2 的数据结构是 [2, 10, [3]],员工 3 的数据结构是 [3, 5, []]。注意虽然员工 3 也是员工 1 的一个下属,但是由于并不是直系下属,因此没有体现在员工 1 的数据结构中。
现在输入一个公司的所有员工信息,以及单个员工 id,返回这个员工和他所有下属的重要度之和。
示例 1:
输入:[[1, 5, [2, 3]], [2, 3, []], [3, 3, []]], 1
输出:11
解释:
员工 1 自身的重要度是 5,他有两个直系下属 2 和 3,而且 2 和 3 的重要度均为 3。因此员工 1 的总重要度是 5 + 3 + 3 = 11。
注意:
- 一个员工最多有一个直系领导,但是可以有多个直系下属
- 员工数量不超过 2000。
解法一
BFS,没啥好说的,憨憨题直接 bugfree
public int getImportance(List<Employee> employees, int id) {
HashMap<Integer,Employee> map=new HashMap<>();
for (Employee e:employees) {
map.put(e.id,e);
}
Queue<Integer> queue=new LinkedList<>();
queue.add(id);
int res=0;
while(!queue.isEmpty()){
Employee cur=map.get(queue.poll());
res+=cur.importance;
List<Integer> subordinates=cur.subordinates;
if (!subordinates.isEmpty()) {
for (int eid:subordinates) {
queue.add(eid);
}
}
}
return res;
}
解法二
DFS,本来不想写的,这类题其实都是树的题变了个说法而已
public int getImportance(List<Employee> employees, int id) {
HashMap<Integer,Employee> map=new HashMap<>();
for (Employee e:employees) {
map.put(e.id,e);
}
return dfs(map,id);
}
public int dfs(HashMap<Integer,Employee> map,int id){
Employee cur=map.get(id);
int res=cur.importance;
for (int eid:cur.subordinates) {
res+=dfs(map,eid);
}
return res;
}
1311. 获取你好友已观看的视频
有 n 个人,每个人都有一个 0 到 n-1 的唯一 id 。
给你数组 watchedVideos 和 friends ,其中 watchedVideos[i] 和 friends[i] 分别表示 id = i 的人观看过的视频列表和他的好友列表。
Level 1 的视频包含所有你好友观看过的视频,level 2 的视频包含所有你好友的好友观看过的视频,以此类推。一般的,Level 为 k 的视频包含所有从你出发,最短距离为 k 的好友观看过的视频。
给定你的 id 和一个 level 值,请你找出所有指定 level 的视频,并将它们按观看频率升序返回。如果有频率相同的视频,请将它们按名字字典序从小到大排列。
示例 1:
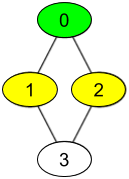
输入:watchedVideos = [["A","B"],["C"],["B","C"],["D"]], friends = [[1,2],[0,3],[0,3],[1,2]], id = 0, level = 1
输出:["B","C"]
解释:
你的 id 为 0 ,你的朋友包括:
id 为 1 -> watchedVideos = ["C"]
id 为 2 -> watchedVideos = ["B","C"]
你朋友观看过视频的频率为:
B -> 1
C -> 2
示例 2:

输入:watchedVideos = [["A","B"],["C"],["B","C"],["D"]], friends = [[1,2],[0,3],[0,3],[1,2]], id = 0, level = 2
输出:["D"]
解释:
你的 id 为 0 ,你朋友的朋友只有一个人,他的 id 为 3 。
提示:
- n == watchedVideos.length == friends.length
- 2 <= n <= 100
- 1 <= watchedVideos[i].length <= 100
- 1 <= watchedVideos[i][j].length <= 8
- 0 <= friends[i].length < n
- 0 <= friends[i][j] < n
- 0 <= id < n
- 1 <= level < n
- 如果 friends[i] 包含 j ,那么 friends[j] 包含 i
解法一
170 周赛的第三题,其实是一道水题,题目意思搞清楚就很简单了
public List<String> watchedVideosByFriends(List<List<String>> watchedVideos, int[][] friends, int id, int level) {
Queue<Integer> queue=new LinkedList<>();
int[] levels=new int[friends.length]; //这里没必要,这里用一个变量就 ok 了
boolean[] visit=new boolean[friends.length];
HashMap<String,Integer> map=new HashMap<>();
List<Integer> flist=new ArrayList<>(); //level 层的朋友
queue.add(id);
visit[id]=true;
while(!queue.isEmpty()){
int cur=queue.poll();
int[] cfs=friends[cur];
for (int i=0;i<cfs.length;i++) {
if (!visit[cfs[i]]) {
queue.add(cfs[i]);
levels[cfs[i]]=levels[cur]+1;
visit[cfs[i]]=true;
if (levels[cfs[i]] == level) {
flist.add(cfs[i]);
}
}
}
}
for (int i=0;i<flist.size();i++) {
List<String> videos=watchedVideos.get(flist.get(i));
for (String v:videos) {
map.put(v,map.getOrDefault(v,0)+1); //map 记录 videos 出现的次数
}
}
//下面几步还是挺老道的
List<String> res=new ArrayList(map.keySet());
res.sort((v1,v2)->{
int c1=map.get(v1);
int c2=map.get(v2);
return c1==c2?v1.compareTo(v2):c1-c2; //相等的时候按照字典序列排序
});
return res;
}
399. 除法求值
给出方程式 A / B = k, 其中 A 和 B 均为代表字符串的变量, k 是一个浮点型数字。根据已知方程式求解问题,并返回计算结果。如果结果不存在,则返回 -1.0。
示例 :
给定 a / b = 2.0, b / c = 3.0
问题:a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
返回 [6.0, 0.5, -1.0, 1.0, -1.0 ]
输入为:vector<pair<string, string>> equations, vector<double>& values, vector<pair<string, string>> queries(方程式,方程式结果,问题方程式), 其中 equations.size() == values.size(),即方程式的长度与方程式结果长度相等(程式与结果一一对应),并且结果值均为正数。以上为方程式的描述。 返回vector<double>类型。
基于上述例子,输入如下:
equations(方程式) = [ ["a", "b"], ["b", "c"] ],
values(方程式结果) = [2.0, 3.0],
queries(问题方程式) = [ ["a", "c"], ["b", "a"], ["a", "e"], ["a", "a"], ["x", "x"] ].
输入总是有效的。你可以假设除法运算中不会出现除数为 0 的情况,且不存在任何矛盾的结果。
解法一
建立图,然后 BFS,这样就简单多了,比并茶集的方法直白多了,随便也学了一下如何建图
//构造图 + BFS/DFS
private Map<String,Map<String,Double>> graph = new HashMap<>();
public void buildGraph(List<List<String>> equations, double[] values){
for (int i = 0; i < values.length; i++) {
graph.computeIfAbsent(equations.get(i).get(0), k -> new HashMap<>()).put(equations.get(i).get(1), values[i]);
graph.computeIfAbsent(equations.get(i).get(1), k -> new HashMap<>()).put(equations.get(i).get(0), 1 / values[i]);
}
}
class Pair{
String key;
double val;
public Pair(String key,double val){
this.key=key;
this.val=val;
}
}
public double bfs(String a,String b){
//讲道理,不管 a,b 是否在 graph 中,只要想等都应该返回 1 吧,这里是考虑了 0 的情况?
if (!graph.containsKey(a) || !graph.containsKey(b)) {
return -1.0;
}
if (a.equals(b)) {
return 1.0;
}
Queue<Pair> queue=new LinkedList<>();
queue.add(new Pair(a,1.0));
HashSet<String> visit=new HashSet<>();
while(!queue.isEmpty()){
Pair cur=queue.poll();
if (!visit.contains(cur.key)) {
visit.add(cur.key);
Map<String,Double> map=graph.get(cur.key);
for (String next:map.keySet()) {
if (b.equals(next)) {
return cur.val*map.get(next);
}
queue.add(new Pair(next,cur.val*map.get(next)));
}
}
}
return -1.0;
}
public double dfs(String a,String b,HashSet<String> visit){
if (!graph.containsKey(a)) {
return -1;
}
if (a.equals(b)) {
return 1;
}
visit.add(a);
Map<String,Double> nextMap=graph.get(a);
for (String next:nextMap.keySet()) {
if (!visit.contains(next)) {
double subres=dfs(next,b,visit);
if (subres!=-1) {
return subres*nextMap.get(next);
}
}
}
return -1;
}
public double[] calcEquation(List<List<String>> equations, double[] values, List<List<String>> queries) {
buildGraph(equations,values);
double[] res=new double[queries.size()];
int index=0;
for (List<String> query:queries) {
HashSet<String> visit=new HashSet<>();
//res[index++]=bfs(query.get(0),query.get(1),visit);
res[index++]=bfs(query.get(0),query.get(1));
}
return res;
}
301. 删除无效的括号
删除最小数量的无效括号,使得输入的字符串有效,返回所有可能的结果。
说明: 输入可能包含了除 ( 和 ) 以外的字符。
示例 1:
输入:"()())()"
输出:["()()()", "(())()"]
示例 2:
输入:"(a)())()"
输出:["(a)()()", "(a())()"]
示例 3:
输入:")("
输出:[""]
解法一
BFS 解法
public List<String> removeInvalidParentheses(String s) {
List<String> res=new ArrayList<>();
Queue<String> queue=new LinkedList<>();
HashSet<String> visit=new HashSet<>();
visit.add(s);
queue.add(s);
boolean flag=false;
while(!queue.isEmpty()){
String cur=queue.poll();
if (isValid(cur)) {
res.add(cur);
flag=true;
}
if (flag) {
continue;
}
for (int i=0;i<cur.length();i++) {
if (cur.charAt(i)=='(' || cur.charAt(i)==')') {
String temp=cur.substring(0,i)+cur.substring(i+1,cur.length());
if (!visit.contains(temp)) {
queue.add(temp);
visit.add(temp);
}
}
}
}
if(res.isEmpty()) res.add("");
return res;
}
public boolean isValid(String s){
int left=0,right=0;
for (int i=0;i<s.length();i++) {
if (s.charAt(i)=='(') {
left++;
}else if (s.charAt(i)==')') {
if (left>0) {
left--;
}else{
return false;
}
}
}
return left==0;
}
还是比较简单,dfs 的解法比较难搞,容易 TLE,这里懒得写了
994. 腐烂的橘子
在给定的网格中,每个单元格可以有以下三个值之一:
- 值 0 代表空单元格;
- 值 1 代表新鲜橘子;
- 值 2 代表腐烂的橘子。
每分钟,任何与腐烂的橘子(在 4 个正方向上)相邻的新鲜橘子都会腐烂。
返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1。
示例 1:

输入:[[2,1,1],[1,1,0],[0,1,1]]
输出:4
示例 2:
输入:[[2,1,1],[0,1,1],[1,0,1]]
输出:-1
解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个正向上。
示例 3:
输入:[[0,2]]
输出:0
解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
提示:
1 <= grid.length <= 101 <= grid[0].length <= 10grid[i][j]仅为0、1或2
解法一
BFS 打卡题,这种解法应该算是比较好的了,2ms
private int[][] diretion={{0,1},{1,0},{0,-1},{-1,0}};
public int orangesRotting(int[][] grid) {
Queue<Pair> queue=new LinkedList<>();
int time=0;
int count=0;
for(int i=0;i<grid.length;i++){
for(int j=0;j<grid[0].length;j++){
if(grid[i][j]==1) count++; //统计好橘子的数量
if(grid[i][j]==2){
queue.add(new Pair(i,j));
}
}
}
if(count==0) return 0;
while(!queue.isEmpty()){
//每一轮的坏橘子数量
int size=queue.size();
time++;
while(size-- >0){
Pair pair=queue.poll();
for (int i=0;i<4;i++) {
int nx=pair.x+diretion[i][0];
int ny=pair.y+diretion[i][1];
if(valid(grid,nx,ny) && grid[nx][ny]==1){
grid[nx][ny]=2;
count--;//好橘子--
queue.add(new Pair(nx,ny));
}
}
if(count==0) return time;
}
}
return -1;
}
class Pair{
int x,y;
public Pair(int x,int y){
this.x=x;
this.y=y;
}
}
public boolean valid(final int[][] grid,int x,int y){
return x>=0 && x<grid.length && y>=0 && y<grid[0].length;
}
解法二
一开始的解法,虽然效率稍微低一点点 4ms,但是 bugfree 了
private int[][] diretion={{0,1},{1,0},{0,-1},{-1,0}};
class Pair{
int x,y;
int step;
public Pair(int x,int y,int step){
this.x=x;
this.y=y;
this.step=step;
}
}
public int orangesRotting(int[][] grid) {
Queue<Pair> queue=new LinkedList<>();
int max=0;
for(int i=0;i<grid.length;i++){
for(int j=0;j<grid[0].length;j++){
if(grid[i][j]==2){
queue.add(new Pair(i,j,0));
}
}
}
while(!queue.isEmpty()){
Pair pair=queue.poll();
//统计一个最大的步数作为结果
//max=Math.max(max,pair.step);
max=pair.step; //最后弹出的哪个就是最大的,这是个递增(非单调)的过程
for (int i=0;i<4;i++) {
int nx=pair.x+diretion[i][0];
int ny=pair.y+diretion[i][1];
if(valid(grid,nx,ny) && grid[nx][ny]==1){
grid[nx][ny]=2;
queue.add(new Pair(nx,ny,pair.step+1));
}
}
}
return check(grid)?max:-1;
}
public boolean check(int[][] grid){
for(int i=0;i<grid.length;i++){
for(int j=0;j<grid[0].length;j++){
if(grid[i][j]==1){
return false;
}
}
}
return true;
}
public boolean valid(final int[][] grid,int x,int y){
return x>=0 && x<grid.length && y>=0 && y<grid[0].length;
}
经过勘误,发现有一处地方有点小问题,已经修改,pair.step 在队列中是一个递增(不单调,会相等)的过程,所以最后弹出的就是最大的
1162. 地图分析
你现在手里有一份大小为 N x N 的『地图』(网格) grid,上面的每个『区域』(单元格)都用 0 和 1 标记好了。其中 0 代表海洋,1 代表陆地,你知道距离陆地区域最远的海洋区域是是哪一个吗?请返回该海洋区域到离它最近的陆地区域的距离。
我们这里说的距离是『曼哈顿距离』( Manhattan Distance):(x0, y0) 和 (x1, y1) 这两个区域之间的距离是 |x0 - x1| + |y0 - y1| 。
如果我们的地图上只有陆地或者海洋,请返回 -1。
示例 1:
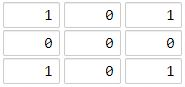
输入:[[1,0,1],[0,0,0],[1,0,1]]
输出:2
解释:
海洋区域 (1, 1) 和所有陆地区域之间的距离都达到最大,最大距离为 2。
示例 2:
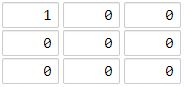
输入:[[1,0,0],[0,0,0],[0,0,0]]
输出:4
解释:
海洋区域 (2, 2) 和所有陆地区域之间的距离都达到最大,最大距离为 4。
提示:
1 <= grid.length == grid[0].length <= 100grid[i][j]不是0就是1
解法一
这题的意思其实求离陆地最远的海洋是那一块,然后返回这个最远的距离,这个题目描述的确实让人迷惑,一会儿最远,一会儿最近,其实题目意思搞懂了就很简单了,其实和上面腐烂的橘子是一样的。多源的 BFS,曼哈顿距离其实就是上下左右走的 step
private int[][] diretion={{1,0},{-1,0},{0,1},{0,-1}};
public int maxDistance(int[][] grid) {
int maxDis=-1;
int m=grid.length,n=grid[0].length;
boolean[][] visit=new boolean[m][n];
Queue<Pair> queue=new LinkedList<>();
for(int i=0;i<m;i++){
for(int j=0;j<n;j++){
if(grid[i][j]==1){
queue.add(new Pair(i,j,0));
visit[i][j]=true;
}
}
}
if(queue.size()==0 || queue.size()==m*n)return -1;
int step=0;
int res=-1;
while(!queue.isEmpty()){
Pair pair=queue.poll();
res=pair.step;
for (int i=0;i<4;i++) {
int nx=pair.x+diretion[i][0];
int ny=pair.y+diretion[i][1];
if(valid(grid,nx,ny) && !visit[nx][ny] && grid[nx][ny]==0){
queue.add(new Pair(nx,ny,pair.step+1));
visit[nx][ny]=true;
}
}
}
return res;
}
class Pair{
int x,y;
int step;
public Pair(int x,int y,int step){
this.x=x;
this.y=y;
this.step=step;
}
}
public boolean valid(final int[][] grid,int x,int y){
return x>=0 && x<grid.length && y>=0 && y<grid[0].length;
}
207. 课程表
你这个学期必须选修 numCourse 门课程,记为 0 到 numCourse-1 。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们:[0,1]
给定课程总量以及它们的先决条件,请你判断是否可能完成所有课程的学习?
示例 1:
输入:2, [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0。所以这是可能的。
示例 2:
输入:2, [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0;并且学习课程 0 之前,你还应先完成课程 1。这是不可能的。
提示:
- 输入的先决条件是由 边缘列表 表示的图形,而不是 邻接矩阵 。详情请参见图的表示法。
- 你可以假定输入的先决条件中没有重复的边。
1 <= numCourses <= 10^5
解法二
学习下拓扑排序,其实核心在于邻接表的构建
public boolean canFinish(int numCourses, int[][] prerequisites) {
int[] indegree=new int[numCourses];
List<List<Integer>> adjacency=new ArrayList<>();
for(int i=0;i<numCourses;i++){
adjacency.add(new ArrayList<>());
}
for(int[] p:prerequisites){
indegree[p[0]]++; //每个节点的入度值
//邻接表,注意这里别搞反了,这里记录的是 p[1] 所有的出度节点
adjacency.get(p[1]).add(p[0]);
}
//课程 id
Queue<Integer> queue=new LinkedList<>();
for(int i=0;i<numCourses;i++){
if(indegree[i]==0){
queue.add(i);
}
}
while(!queue.isEmpty()){
int cid=queue.poll();
numCourses--;
for (int id:adjacency.get(cid)) { //cid --> id
//该节点的所有邻接节点入度--
indegree[id]--;
if(indegree[id]==0){
queue.add(id);
}
}
}
return numCourses==0;
}
210. 课程表 II
现在你总共有 n 门课需要选,记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们:[0,1]
给定课程总量以及它们的先决条件,返回你为了学完所有课程所安排的学习顺序。
可能会有多个正确的顺序,你只要返回一种就可以了。如果不可能完成所有课程,返回一个空数组。
示例 1:
输入:2, [[1,0]]
输出:[0,1]
解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
示例 2:
输入:4, [[1,0],[2,0],[3,1],[3,2]]
输出:[0,1,2,3] or [0,2,1,3]
解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
说明:
- 输入的先决条件是由边缘列表表示的图形,而不是邻接矩阵。详情请参见 图的表示法。
- 你可以假定输入的先决条件中没有重复的边。
提示:
- 这个问题相当于查找一个循环是否存在于有向图中。如果存在循环,则不存在拓扑排序,因此不可能选取所有课程进行学习。
- 通过 DFS 进行拓扑排序 - 一个关于 Coursera 的精彩视频教程(21 分钟),介绍拓扑排序的基本概念。
- 拓扑排序也可以通过 BFS 完成。
解法一
BFS 做法,和上面一样
//BFS 拓扑排序
public int[] findOrder(int numCourses, int[][] prerequisites) {
int[] indegree=new int[numCourses]; //入度数
List<List<Integer>> adjacency=new ArrayList<>();
for(int i=0;i<numCourses;i++){
adjacency.add(new ArrayList<>());
}
for(int[] pre:prerequisites){
indegree[pre[0]]++;
adjacency.get(pre[1]).add(pre[0]);
}
int k=0;
int[] res=new int[numCourses];
Queue<Integer> queue=new LinkedList<>();
for(int i=0;i<numCourses;i++){
if(indegree[i]==0){
queue.add(i);
}
}
while(!queue.isEmpty()){
int cur=queue.poll();
res[k++]=cur;
for(int c:adjacency.get(cur)){
indegree[c]--;
if(indegree[c]==0){
queue.add(c);
}
}
}
return k==numCourses?res:new int[0];
}
解法二
DFS 的做法,比 BFS 更有意思一点,其实就是个不断判环的过程,图相关的还是不太熟悉啊
//DFS 的解法
int k=0;
public int[] findOrder(int numCourses, int[][] prerequisites) {
List<List<Integer>> adjacency=new ArrayList<>();
for(int i=0;i<numCourses;i++){
adjacency.add(new ArrayList<>());
}
int[] mark=new int[numCourses];
int[] res=new int[numCourses];
for(int[] pre:prerequisites){
adjacency.get(pre[0]).add(pre[1]); //注意这个区别
}
for (int i=0;i<numCourses;i++) {
if(dfs(adjacency,i,mark,res)) return new int[0];
}
return res;
}
public boolean dfs(List<List<Integer>> adj,int cur,int[] mark,int[] res){
if(mark[cur]==1) return true; //正在访问
if(mark[cur]==2) return false; //节点已经访问完(之前已经学了)
mark[cur]=1;
for(int c:adj.get(cur)){
if(dfs(adj,c,mark,res)){
return true;
}
}
mark[cur]=2;
//cur 的先决课程是没环的,所以可以学 cur
res[k++]=cur;
return false;
}
365. 水壶问题
Difficulty: 中等
有两个容量分别为 _x_升 和 _y_升 的水壶以及无限多的水。请判断能否通过使用这两个水壶,从而可以得到恰好 _z_升 的水?
如果可以,最后请用以上水壶中的一或两个来盛放取得的 _z 升 _水。
你允许:
- 装满任意一个水壶
- 清空任意一个水壶
- 从一个水壶向另外一个水壶倒水,直到装满或者倒空
示例 1: (From the famous )
输入:x = 3, y = 5, z = 4
输出:True
示例 2:
输入:x = 2, y = 6, z = 5
输出:False
解法一
暴力 BFS 的解法
public boolean canMeasureWater(int x, int y, int z) {
Queue<int[]> queue = new LinkedList<>();
int capX = x;
int capY = y;
queue.add(new int[]{x, y});
while(!queue.isEmpty()) {
int[] cur = queue.poll();
int cx = cur[0];
int cy = cur[1];
if (cx==z || cy==z || cx+cy==z) {
return true;
}
//清空 x
addQueue(0, cy, queue);
//清空 y
addQueue(cx, 0, queue);
//装满 x
addQueue(capX, cy, queue);
//装满 y
addQueue(cx, capY, queue);
//x-->y
addQueue(Math.max(0, cx-capY+cy), Math.min(capY, cy+cx), queue);
//y-->x
addQueue(Math.min(capX, cy+cx), Math.max(0, cy-capY+cx), queue);
}
return false;
}
public void addQueue(int x, int y, Queue<int[]> queue){
long hashCode = x * (long)1e9+7 + y;
if (!visit.contains(hashCode)) {
queue.add(new int[]{x, y});
visit.add(hashCode);
}
}
解法二 数学解法,涉及到一些数学定理(贝祖定理),我也不是很懂(就是搞懂过两天也忘了)
public boolean canMeasureWater(int x, int y, int z) {
if(x+y<z) return false;
if(x==0 || y==0) return z==0 || x+y==z;
return z%gcd(x,y)==0;
}
public int gcd(int a,int b){
if(b==0) return a;
return gcd(b,a%b);
}
单调栈
单独开辟出新的专题 LeetCode 单调栈