LeetCode回溯&递归

2019-10-10 约 26823 字预计阅读 54 分钟

17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）注意 1 不对应任何字母

示例：

输入："23"
输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

说明： 尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

解法一

String[] letter={" ","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};

private List<String> res=new LinkedList<>();

public List<String> letterCombinations(String digits) {
    //空字符串要注意
    if ("".equals(digits)) return res;
    letterCombinations(digits,0,"");
    return res;
}

public void letterCombinations(String digits,int index,String str) {
    //递归出口，当 index==digits 的长度的时候就说明走到尽头了
    //需要回头尝试其他的情况
    if (index==digits.length()) {
        res.add(str);
        return;
    }
    //当前字符对应的字母组合
    char[] ls=letter[digits.charAt(index)-48].toCharArray();
    //遍历每种可能，其实就是 DFS
    for (int i=0;i<ls.length;i++) {
        letterCombinations(digits,index+1,str+ls[i]);
    }
    return;
}

可想而知，这个算法的时间复杂度相当高，3^N * 4^M = O(2^N) M 是能表示 3 个字符的数字个数，N 是表示 4 个字符的数字个数，指数级别的算法，但是也没有其他别的比较好的算法了

93. 复原 IP 地址

给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

示例：

输入："25525511135"
输出：["255.255.11.135", "255.255.111.35"]

解法一

其实还是有一个大致的思路，但是没写出来，很多细节不知道咋处理

public List<String> restoreIpAddresses(String s) {
    restoreIpAddresses(s,0,"",0);
    return res;
}

LinkedList<String> res=new LinkedList<>();

public void restoreIpAddresses(String s,int index,String des,int count) {
    if (count>4) {
        return;
    }
    //到字符串末尾了
    if (index==s.length()) {
        if (count==4) {
            res.add(des.substring(0,des.length()-1));    
        }
        return;
    }
    //如果为 0 就不用切分了，这里就相当于直接跳过
    if (s.charAt(index)=='0') {
        restoreIpAddresses(s,index+1,des+"0.",count+1);
    }else{
        //不为 0 就需要继续切分为 1，2，3
        //切分过程中需要注意要小于 255, 同时需要一个计数器来判度是否终止
        for (int i=1;i<4;i++) {
            if (index+i<=s.length()) {
                String temp=s.substring(index,index+i);
                if (Integer.valueOf(temp)<=255){
                    restoreIpAddresses(s,index+i,des+temp+".",count+1);    
                }
            }
        }
    }
}

UPDATE: 2020.8.9

今天的打卡题，用 go 重写了下，比之前写的好多了，不过一开始忘了处理 0WA 了一发，然后懒的对长度不合法的剪枝又 T 了一发。

func restoreIpAddresses(s string) []string {
    var res []string
    if len(s) < 4 || len(s) > 12 {
        return res
    }
    var dfs func(s string, lis []string)
    dfs = func(s string, lis []string) {
        if s == "" {
            if len(lis) == 4 {
                res = append(res, strings.Join(lis, "."))
            }
            return
        }
        //s 未遍历完就集齐了 4 块
        if len(lis) >= 4 {
            return
        }
        for i := 1; i <= 3; i++ {
            if i <= len(s) && check(s[:i]) {
                lis = append(lis, s[:i])
                dfs(s[i:], lis)
                lis = lis[:len(lis)-1]
                //前导 0 的处理，读取 0 之后就不再向后扩展
                if s[:i] == "0" {
                    return
                }
            }
        }
    }
    dfs(s, []string{})
    return res
}

func check(s string) bool {
    if ns, _ := strconv.Atoi(s); ns <= 255 {
        return true
    }
    return false
}

131. 分割回文串

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例：

输入："aab"
输出：
[
  ["aa","b"],
  ["a","a","b"]
]

解法一

总算自己完整做了一题出来了

public List<List<String>> partition(String s) {
    partition(s,0,new ArrayList());
    return res;
}   

List<List<String>> res=new ArrayList<>();

public void partition(String s,int index,List<String> lis) {
    if (index==s.length()) {
        //注意这里要 copy 一个 list 不能直接添加 lis
        //lis 引用的对象后面还会继续变化，最后会变为 null
        res.add(new ArrayList(lis));
        return;
    }
    for (int i=index+1;i<=s.length();i++) {
        String temp=s.substring(index,i);
        //System.out.println(index+"="+i+"="+temp);
        if (isPalind(temp)) {
            lis.add(temp);
            partition(s,i,lis);
            //不能直接 remove(temp), 主要是会有重复的字符，所以会导致最后的顺序不一致，而且效率也很低
            //lis.remove(temp);
            lis.remove(lis.size()-1);
        }
    }
}

public boolean isPalind(String s){
    for (int i=0,j=s.length()-1;i<=j;i++,j--) {
        if (s.charAt(i)!=s.charAt(j)) {
            return false;
        }
    }
    return true;
}

4ms，93%，其实就是暴力回溯，还是挺简单的，一开始忘了remove()，直接把所有结果打出来了，然后一直在想怎么调整递归的结构。DFS 基本的套路都忘了😂

46. 全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例：

输入：[1,2,3]
输出：
[
  [1,2,3],
  [1,3,2],
  [2,1,3],
  [2,3,1],
  [3,1,2],
  [3,2,1]
]

解法一

经典的全排列问题，熟悉了 DFS 套路之后都挺简单的，注意回溯就行了

public List<List<Integer>> permute(int[] nums) {
    if (nums==null || nums.length<=0) {
        return res;
    }
    boolean[] visit=new boolean[nums.length];
    permute(nums,new ArrayList(),visit);
    return res;
}

private List<List<Integer>> res=new ArrayList<>();

public void permute(int[] nums,List<Integer> lis,boolean[] visit) {
    if (lis.size()==nums.length) {
        res.add(new ArrayList(lis));
        return;
    }
    for (int i=0;i<nums.length;i++) {
        if (visit[i]) continue;
        lis.add(nums[i]);
        visit[i]=true;
        permute(nums,lis,visit);
        //回溯
        visit[i]=false;
        lis.remove(lis.size()-1);
    }
}

60. 第 k 个排列

给出集合 [1,2,3,…,n]，其所有元素共有 n! 种排列。

按大小顺序列出所有排列情况，并一一标记，当 n = 3 时，所有排列如下：

"123"
"132"
"213"
"231"
"312"
"321"

给定 n 和 k，返回第 k 个排列。

说明：

给定 n 的范围是 [1, 9]。
给定 k 的范围是 [1, n!]。

**示例 1: **

输入：n = 3, k = 3
输出："213"

示例 2:

输入：n = 4, k = 9
输出："2314"

解法一

public String getPermutation(int n, int k) {
    boolean[] visit=new boolean[n+1];
    getPermutation(n,k,0,visit,new StringBuilder(""));
    return res.get(k-1).toString();
}

private List<StringBuilder> res=new LinkedList<>();

public void getPermutation(int n, int k,int count,boolean[] visit,StringBuilder str) {
    if (count == n) {
        res.add(new StringBuilder(str));
        return;
    }
    if (res.size()==k) {
        return;
    }
    for (int i=1;i<=n;i++) {
        if (!visit[i]) {
            str.append(i);
            visit[i]=true;
            getPermutation(n,k,count+1,visit,str);
            visit[i]=false;
            str.delete(str.length()-1,str.length());
        }
    }
}

偶然发现这一题并没有记录，之前没有记录的原因肯定是因为方法太垃圾了，这题最优解是 康托展开，说实话，暂时并不想去了解😂，后面有时间再说吧

5374. 长度为 n 的开心字符串中字典序第 k 小的字符串

一个「开心字符串」定义为：

仅包含小写字母 [‘a’, ‘b’, ‘c’].
对所有在 1 到 s.length - 1 之间的 i ，满足 s[i] != s[i + 1] （字符串的下标从 1 开始）。

比方说，字符串 “abc”，“ac”，“b” 和 “abcbabcbcb” 都是开心字符串，但是 “aa”，“baa” 和 “ababbc” 都不是开心字符串。

给你两个整数 n 和 k ，你需要将长度为 n 的所有开心字符串按字典序排序。

请你返回排序后的第 k 个开心字符串，如果长度为 n 的开心字符串少于 k 个，那么请你返回空字符串。

示例 1：

输入：n = 1, k = 3
输出："c"
解释：列表 ["a", "b", "c"] 包含了所有长度为 1 的开心字符串。按照字典序排序后第三个字符串为 "c" 。

示例 2：

输入：n = 1, k = 4
输出：""
解释：长度为 1 的开心字符串只有 3 个。

示例 3：

输入：n = 3, k = 9
输出："cab"
解释：长度为 3 的开心字符串总共有 12 个 ["aba", "abc", "aca", "acb", "bab", "bac", "bca", "bcb", "cab", "cac", "cba", "cbc"] 。第 9 个字符串为 "cab"

示例 4：

输入：n = 2, k = 7
输出：""

示例 5：

输入：n = 10, k = 100
输出："abacbabacb"

提示：

1 <= n <= 10
1 <= k <= 100

解法一

补下 24th 双周赛 T3，和上面一题很类似，直接暴力回溯了

public String getHappyString(int n, int k) {
    dfs("a",n,k);
    dfs("b",n,k);
    dfs("c",n,k);
    return res;
}

private int count=0;

private String res="";

public void dfs(String cur,int n,int k){
    if(!"".equals(res)) return;
    if(cur.length()==n){
        count++;
        if(count==k){
            res=cur;
        }
        return;
    }
    char last=cur.charAt(cur.length()-1);
    if(last=='a'){
        dfs(cur+'b',n,k);
        dfs(cur+'c',n,k);
    }
    if(last=='b'){
        dfs(cur+'a',n,k);
        dfs(cur+'c',n,k);
    }
    if(last=='c'){
        dfs(cur+'a',n,k);
        dfs(cur+'b',n,k);
    }
}

其实直接队列模拟也是可以的，模拟的效率应该会更高一些，好像也可以直接构造出来

47. 全排列 II

给定一个可包含重复数字的序列，返回所有不重复的全排列。

示例：

输入：[1,1,2]
输出：
[
  [1,1,2],
  [1,2,1],
  [2,1,1]
]

解法一

开始我很纠结这题，后来想通了，其实就是去重，遇到已经存在于结果中相同的元素就直接跳过就行了

public List<List<Integer>> permuteUnique(int[] nums) {
    if (nums==null || nums.length<=0) {
        return res;
    }
    //Arrays.sort(nums); 解法二需要先排序
    boolean[] visit=new boolean[nums.length];
    permuteUnique(nums,new ArrayList(),visit);
    return res;
}

private List<List<Integer>> res=new ArrayList<>();

public void permuteUnique(int[] nums,List<Integer> lis,boolean[] visit){
    HashSet<Integer> set=new HashSet<>();
    if (lis.size()==nums.length) {
        res.add(new ArrayList(lis));
        return;
    }
    for (int i=0;i<nums.length;i++) {
        if (!visit[i] && !set.contains(nums[i])) {
            lis.add(nums[i]);
            visit[i]=true;
            set.add(nums[i]);
            permuteUnique(nums,lis,visit);
            visit[i]=false;
            lis.remove(lis.size()-1);
        }
    }
}

//需要排序
public void permuteUnique2(int[] nums,List<Integer> lis,boolean[] visit){
    if (lis.size()==nums.length) {
        res.add(new ArrayList(lis));
        return;
    }
    for (int i=0;i<nums.length;i++) {
        //剪枝去重，和前一个元素比较
        //Bug 警告，应该写！visit[i-1]
        if (i>0&&nums[i]==nums[i-1] && !visit[i-1]) 
            continue;
        if (!visit[i]) {
            lis.add(nums[i]);
            visit[i]=true;
            permuteUnique2(nums,lis,visit);
            visit[i]=false;
            lis.remove(lis.size()-1);
        }
    }
}

关于去重的方式，其实我们可以从回溯的根节点来考虑，也就是我们考虑最顶层的【1，1，2】的遍历情况，每一次遍历实际上都是在找以当前元素开头的排列，当第一次已经遍历完 1 开头的所以排列后，后面的循环再碰到 1 自然就可以直接跳过了，所以我们可以在一次遍历中用 HashMap 来去重，来保证一次循环中不会有重复的元素被选取，其实也只有这题可以用 HashSet，因为这里排列是讲究顺序的，循序完全一样才是重复，后面的题都是不讲究顺序的，都需要排序才能去重，具体后面再分析

我首先想到的就是 Hash 表，这里翻了下评论区好像都是用的第二种方式去重的，难道用 HashSet 不好么😂，第二种必须要先排序，保证相同的元素都聚在一起，方便判断，这种题在纸上画一画递归树其实就很清楚了

Bug 警告

这里 !visit[i-1]和 visit[i-1]对于这题来说并不影响正确性，但是你如果将生成的过程打印出来对比下就知道为啥了，具体的请看下面 1079. 活字印刷的解释

1286. 字母组合迭代器

请你设计一个迭代器类，包括以下内容：

一个构造函数，输入参数包括：一个有序且字符唯一的字符串 characters（该字符串只包含小写英文字母）和一个数字 combinationLength 。
函数 next() ，按字典序返回长度为 combinationLength 的下一个字母组合。
函数 hasNext() ，只有存在长度为 combinationLength 的下一个字母组合时，才返回 True；否则，返回 False。

示例：

CombinationIterator iterator = new CombinationIterator("abc", 2); // 创建迭代器 iterator

iterator.next(); // 返回 "ab"
iterator.hasNext(); // 返回 true
iterator.next(); // 返回 "ac"
iterator.hasNext(); // 返回 true
iterator.next(); // 返回 "bc"
iterator.hasNext(); // 返回 false

提示：

1 <= combinationLength <= characters.length <= 15
每组测试数据最多包含 10^4 次函数调用。
题目保证每次调用函数 next 时都存在下一个字母组合。

解法一

唉，真的菜，好久没写回溯了，又給忘了，这题开始被别人误导了，以为是下一个排列，然后就一直在想怎么去求 next，其实根本就不用这样。..

private LinkedList<String> res=new LinkedList<>();

//abc
public CombinationIterator(String characters, int combinationLength) {
    dfs("",combinationLength,0,0,characters);
}

public String next() {
    return res.pollFirst();
}

public void dfs(String cur,int len,int index,int count,String source) {
    if (count == len) {
        res.add(cur); //直接根据 cur 得长度判断就 ok 了
        return;
    }
    for (int i=index;i<source.length();i++) {
        dfs(cur+source.charAt(i),len,i+1,count+1,source);
    }
}

public boolean hasNext() {
    return !res.isEmpty();
}

回头开了下之前的代码，发现都写得不好，很喜欢加个 count 统计数量，其实直接根据 cur 得长度判断就可以了

77. 组合

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例：

输入：n = 4, k = 2
输出：
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

解法一

其实一开始没写出剪枝的代码，看了一点提示后才写出了下面的的第一种剪枝的方法

public List<List<Integer>> combine(int n, int k) {
    if (k>n || n<=0 ||k<=0) {
        return res;
    }
    //boolean[] visit=new boolean[n+1];
    combine(n,k,1,new ArrayList(),0);
    return res;
}   

private List<List<Integer>> res=new ArrayList<>();

//剪枝优化 1
public void combine(int n, int k,int index,List<Integer> lis,int count) {
    if (count==k) {
        res.add(new ArrayList(lis));
        return;
    }
    //1 2 3 4 | 3
    //index = 3 k=3  n=4 count=0 (3 为头，显然是不行的，肯定会和前面重复） --> 3<=3
    //index = 3 k=3  n=4 count=1 (3 为第二个，是可行的） --> 3 <= 2
    if (n-index+2<=k-count) {
        return;
    }
    for (int i=index;i<=n;i++) {
        lis.add(i);
        combine(n,k,i+1,lis,count+1);
        //回溯的关键
        lis.remove(lis.size()-1);
    }
}

//剪枝优化 2
public void combine4(int n, int k,int index,List<Integer> lis,int count) {
    if (count==k) {
        res.add(new ArrayList(lis));
        return;
    }
    //循环的区间至少要有 k-count 个元素 也就是 [i,N] 之间至少要有 k-count 个元素
    //N-i+1>=k-count --> i<=n-(k-count)+1
    for (int i=index;i<=n-(k-count)+1;i++) {
        lis.add(i);
        combine4(n,k,i+1,lis,count+1);
        //回溯的关键
        lis.remove(lis.size()-1);
    }
}

举个例子1，2，3，4 k=3 其实在循环 n=3 的时候就可以结束了，因为后面已经没有那么多元素可以和 3 构成组合了

39. 组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合，candidates 中的数字可以无限制重复被选取

说明：

所有数字（包括 target）都是正整数。
解集不能包含重复的组合。

示例 1:

输入：candidates = [2,3,6,7], target = 7,
所求解集为：
[
  [7],
  [2,2,3]
]

示例 2:

输入：candidates = [2,3,5], target = 8,
所求解集为：
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]

解法一

没有任何剪枝处理的回溯，感觉一开始就想好怎么剪枝还是不太容易，这题其实和上面的组合很类似，值得注意的就是子递归调用的时候传递的 index 参数

public List<List<Integer>> combinationSum(int[] candidates, int target) {
    if (candidates==null || candidates.length<=0) {
        return res;
    }
    combinationSum(candidates,target,0,0,new ArrayList());
    return res;
}

private List<List<Integer>> res=new ArrayList<>();

public void combinationSum(int[] candidates, int target,int index,int sum,List<Integer> lis) {
    if (sum>target) {
        return;
    }
    if (target==sum) {
        res.add(new ArrayList(lis));
        return;
    }
    //这里一次循环其实就确定了包含 i 的所有可能解，所以起点是 index 不是 0
    for (int i=index;i<candidates.length;i++) {
        //跳过比 target 大的
        if (candidates[i]>target) continue;
        sum+=candidates[i];
        lis.add(candidates[i]);
		//其实主要就是搞清楚每次从哪里开始，以及每次循环的作用
        //可以重复选取自己，所以子递归也从 i 开始而不是 i+1
        combinationSum(candidates,target,i,sum,lis);
        sum-=candidates[i];
        lis.remove(lis.size()-1);
    }
}

解法二

剪枝优化，主要是要先排个序，这样如果在循环过程中，累加和已经大于 target 了就直接 return，如果不排序就不能 return，因为无法确保后面会不会更小的元素

public List<List<Integer>> combinationSum(int[] candidates, int target) {
    if (candidates==null || candidates.length<=0) {
        return res;
    }
    //排序，方便剪枝
    Arrays.sort(candidates);
    combinationSum(candidates,target,0,0,new ArrayList());
    return res;
}

private List<List<Integer>> res=new ArrayList<>();

//剪枝优化 2
public void combinationSum(int[] candidates, int target,int index,int sum,List<Integer> lis) {
    if (sum>target) {
        return;
    }
    if (target==sum) {
        res.add(new ArrayList(lis));
        return;
    }
    for (int i=index;i<candidates.length;i++) {
        if (sum+candidates[i]>target) return;
        sum+=candidates[i];
        lis.add(candidates[i]);
        //注意这里传递进去的 index 是 i
        combinationSum(candidates,target,i,sum,lis);
        sum-=candidates[i];
        lis.remove(lis.size()-1);
    }
}

这两天状态还可以啊，好多题都可以完全独立的写出来了😁

40. 组合总和 II

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：

所有数字（包括目标数）都是正整数。
解集不能包含重复的组合。

示例 1:

输入：candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为：
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

示例 2:

输入：candidates = [2,5,2,1,2], target = 5,
所求解集为：
[
  [1,2,2],
  [5]
]

解法一

public List<List<Integer>> combinationSum2(int[] candidates, int target) {
    if (candidates ==null || candidates.length<=0) {
        return res;
    }
    Arrays.sort(candidates);
    combinationSum2(candidates,target,0,new ArrayList());
    return res;
}

public void combinationSum2(int[] candidates, int target,int index,List<Integer> lis) {
    /*if (target<0) {
            return;
        }*/
    if (target==0) {
        res.add(new ArrayList(lis));
        return;
    }

    for (int i=index;i<candidates.length;i++) {
        //注意这里 i>index
        if (i>index && candidates[i]==candidates[i-1]  ) continue;
        //排过序的，可以直接 return
        if (target-candidates[i]<0) return;
        lis.add(candidates[i]);
        combinationSum2(candidates,target-candidates[i],i+1,lis);
        lis.remove(lis.size()-1);
    }
}

回溯其实值得注意的就那几个点，循环的起点，下次递归的起点，回溯，出口，这几个点都搞清楚了其实就很简单了，关键的地方就是如何去重

这题如果参照上面 [全排列 2](## 47. 全排列 II) 的第一种 HashSet 的去重方式的话，明显是有问题的，HashSet 的去重方式只能保证每一次循环中不会有重复的元素被选取，但是这题即使循环中没有重复的元素被选取，结果仍然会有重复

比如 10,1,2,7,6,1,5 遍历 1 的时候会得到1 2 5，后续遍历 2 的时候又会得到一个 2 1 5 ，但是其实在第一次循环的时候就已经找到了所有包含 1 的解，后面循环中包含 1 的解其实都重复了，如果我们排序后就变为 1 1 2 5 6 7 10 把相同的元素聚集到一起，一方面可以去重，另一方面还可以剪枝，在第一次循环的时候就已经找到了所有的带有 1 的解，后面的连着的 1 都可以跳过了，后续就不会再有包含 1 的解了，如果不排序，后面仍然会有包含 1 的解

216. 组合总和 III

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

所有数字都是正整数。
解集不能包含重复的组合。

示例 1:

输入：k = 3, n = 7
输出：[[1,2,4]]

示例 2:

输入：k = 3, n = 9
输出：[[1,2,6], [1,3,5], [2,3,4]]

解法一

感觉比上面两题还简单一点，可以直接剪枝

//UPDATE: 2020.9.11
func combinationSum3(k int, n int) [][]int {
    var res [][]int
    var dfs func(idx int, sum int, lis []int)
    dfs = func(idx int, sum int, lis []int) {
        if len(lis) > k {
            return
        }
        if sum == n && len(lis) == k {
            dest := make([]int, len(lis))
            copy(dest, lis)
            res = append(res, dest)
            return
        }
        for i := idx; i <= 9; i++ {
            if sum + i > n {
                return
            }
            dfs(i+1, sum+i, append(lis, i))
        }
    }
    dfs(1, 0, []int{})
    return res
}

解法二（UPDATE：2020.9.11）

学了下二进制枚举子集的方法，很简洁

func combinationSum3(k int, n int) [][]int {
    var res [][]int
    for i := 0; i < (1<<9); i++ {
        var sum, cnt = 0, 0
        var lis []int
        for j := 0; j < 9; j++ {
            if i & (1<<j) != 0 {
                sum += j+1
                cnt++
                lis = append(lis, j+1)
            }
        }
        if sum == n && cnt == k {
            res = append(res, lis)   
        }
    }
    return res
}

78. 子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

**说明：**解集不能包含重复的子集。

示例：

输入：nums = [1,2,3]
输出：
[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

解法一

private List<List<Integer>> res=new ArrayList<>();

public List<List<Integer>> subsets(int[] nums) {
    if (nums==null || nums.length<=0) {
        return res;
    }
    subsets(nums,0,new ArrayList());
    return res;
}

public void subsets(int[] nums,int index,List<Integer> lis) {
    //if (index<=nums.length) {
        res.add(new ArrayList(lis));
    //}
    for (int i=index; i<nums.length;i++) {
        lis.add(nums[i]);
        subsets(nums,i+1,lis);
        lis.remove(lis.size()-1);
    }
}

简单的回溯，注意收集结果的时机就行

Update: 2020.6.20

增加一个 go 的写法

func subsets(nums []int) [][]int {
    var res [][]int
    var lis []int
    var dfs func(index int)
    dfs = func(index int){
        dest:=make([]int,len(lis))
        copy(dest,lis)
        res=append(res,dest)
        for i:=index;i<len(nums);i++{
            lis=append(lis,nums[i])
            dfs(i+1)
            lis=lis[:len(lis)-1]
        }
    }
    dfs(0)
    return res
}

解法二

BFS，类似于二叉树层次遍历，首先初始化一个空的 list，后面每次迭代都将 list 中的所有元素都取出来加上当前元素，再重新加入到 list 中

public List<List<Integer>> subsets(int[] nums) {
    List<List<Integer>> queue=new ArrayList<>();
    if (nums==null || nums.length<=0) {
        return queue;
    }
    queue.add(new ArrayList());
    for (int i=0;i<nums.length;i++) {
        int next=queue.size();
        for (int j=0;j<next;j++) {
            List<Integer> temp=new ArrayList(queue.get(j));
            temp.add(nums[i]);
            queue.add(temp);
        }
    }
    return queue;
}

解法三（UPDATE: 2020.9.11）

二进制枚举子集

func subsets(nums []int) [][]int {
    var n = len(nums)
    var res [][]int
    for i := 0; i < (1<<n); i++ {
        var lis []int
        for j := 0; j < n; j++ {
            if i & (1<<j) != 0 {
                lis = append(lis, nums[j])
            }
        }
        res = append(res, lis)
    }
    return res
}

90. 子集 II

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

**说明：**解集不能包含重复的子集。

示例：

输入：[1,2,2]
输出：
[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

解法一

和 40 题很类似，主要就是这个去重的操作，比如题目给的 case，[1,2,2] 已经有序了，在选择第一个 2 的时候其实就已经将所有包含 2 的子集都求出来了，后面的 2 就可以直接跳过，当然这里 1，2，2 本身就是有序的，试想如果是2,1,2 遍历第一个 2 会将所有包含 2 的子集求出来，但是遍历到 1 的时候会将第三个 2 包含进来，也就是1，2 这个解，但是前面已经求出了[2,1] 这就重复了，排序就是为了将相同的元素聚合到一起，这样遇到相同的元素就跳过，后面的元素就不会再包含已经遍历过的元素了

public List<List<Integer>> subsetsWithDup(int[] nums) {
    if (nums==null || nums.length<=0) {
        return res;
    }
    //需要先排序，便于跳过相同的元素
    Arrays.sort(nums);
    subsets(nums,0,new ArrayList());
    return res;
}

private  List<List<Integer>> res=new ArrayList<>();

public void subsets(int[] nums,int index,List<Integer> lis) {
    res.add(new ArrayList(lis));
    for (int i=index;i<nums.length;i++) {
        if (i>index && nums[i] == nums[i-1]) {
            continue;
        }
        lis.add(nums[i]);
        subsets(nums,i+1,lis);
        lis.remove(lis.size()-1);
    }
}

Update: 2020.6.20

用 go 重写了一遍，复习下

func subsetsWithDup(nums []int) [][]int {
    sort.Ints(nums)
    var res [][]int
    var lis []int
    var dfs func(index int)
    dfs = func(index int){
        dest:=make([]int,len(lis))
        copy(dest,lis)
        res=append(res,dest)
        for i:=index;i<len(nums);i++{
            if i>index && nums[i]==nums[i-1]{
                continue
            }
            lis=append(lis,nums[i])
            dfs(i+1)
            lis=lis[:len(lis)-1]
        }
    }
    dfs(0)
    return res
}

357. 计算各个位数不同的数字个数

给定一个非负整数 n，计算各位数字都不同的数字 x 的个数，其中 0 ≤ x < 10n 。

示例：

输入：2
输出：91 
解释：答案应为除去 11,22,33,44,55,66,77,88,99 外，在 [0,100) 区间内的所有数字。

解法一

这里要存个疑问，这里的回溯记忆化应该是错的，可能是数据太少了，没测试出来，但是居然真的提高了效率。这就很诡异

//这种可以做记忆化，0ms
Integer[] cache=null;

public int countNumbersWithUniqueDigits2(int n) {
    boolean[] visit=new boolean[10];
    cache=new Integer[n+1];
    int res=0;
    if (n==0) return 1;
    for (int i=1;i<=9;i++) { //不考虑 0 开头的
        visit[i]=true;
        res+=countNumbersWithUniqueDigits2(n,visit,1);
        visit[i]=false;
    }
    return res+1; //加的是 0 这种情况
}

//[index,n](位数)区间内，能构成最多的不重复数字
public int countNumbersWithUniqueDigits2(int n,boolean[] visit,int index){
    if (index==n) { //没得选，只有一种
        return 1;
    }
    if (cache[index]!=null) {
        return cache[index];
    }
    int count=1;
    for (int i=0;i<=9;i++) {
        if (!visit[i]) {
            visit[i]=true;
            count+=countNumbersWithUniqueDigits2(n,visit,index+1);
            visit[i]=false;
        }
    }
    return cache[index]=count;
}

我都不好意思放到回溯专题中，开始写了个贼脑残的回溯 451ms，实在不好意思放上来

解法二

//数学方法（初中数学）
public int countNumbersWithUniqueDigits3(int n){
    if (n==0) return 1;
    if (n>10) return 0;
    int res=10,count=9; //i=1 的情况
    for (int i=2;i<=n;i++) {
        count*=(11-i); //9*9*8*7*6*5.....
        res+=count;
    }
    return res;
}

说实话，这种方法我一开始写第一种很脑残的回溯的时候推出来了的，但是我居然没意识到。

89. 格雷编码

格雷编码是一个二进制数字系统，在该系统中，两个连续的数值仅有一个位数的差异。

给定一个代表编码总位数的非负整数 n，打印其格雷编码序列。格雷编码序列必须以 0 开头。

示例 1:

输入：2
输出：[0,1,3,2]
解释：
00 - 0
01 - 1
11 - 3
10 - 2

对于给定的 n，其格雷编码序列并不唯一。
例如，[0,2,3,1] 也是一个有效的格雷编码序列。

00 - 0
10 - 2
11 - 3
01 - 1

示例 2:

输入：0
输出：[0]
解释：我们定义格雷编码序列必须以 0 开头。
     给定编码总位数为 n 的格雷编码序列，其长度为 2n。当 n = 0 时，长度为 20 = 1。
     因此，当 n = 0 时，其格雷编码序列为 [0]。

解法一

又一个脑残做法。

public List<Integer> grayCode3(int n) {
    List<Integer> res=new ArrayList<>();
    res.add(0);
    int max=(1<<n)-1; //注意优先级
    boolean[] visit=new boolean[max+1];
    grayCode3(max,res,visit);
    return res;
}

public boolean grayCode3(int max,List<Integer> lis,boolean[] visit) {
    if (lis.size()>max) { // list.size()==max+1 eg. when max=3 the list.size()=4
        return true;
    }
    int last=lis.get(lis.size()-1);
    for (int i=1;i<=max;i++) {
        if (!visit[i] && Integer.bitCount(i^last)==1) {
            lis.add(i);
            visit[i]=true;
            if(grayCode3(max,lis,visit)){
                return true;
            }
            lis.remove(lis.size()-1);
            visit[i]=false;
        }
    }
    return false;
}

解法二

正常的回溯，每次修改一位，直接生成下一个可能的格雷码，而不是向上面一样一个个遍历。

//常规回溯
public List<Integer> grayCode2(int n) {
    List<Integer> res=new ArrayList<>();
    boolean[] visit=new boolean[1<<n];
    res.add(0);
    visit[0]=true;
    grayCode2(n,res,visit,0);
    return res;
}

public boolean grayCode2(int n,List<Integer> lis,boolean[] visit,int last) {
    if (lis.size()>=(1<<n)) { // list.size()==max+1 eg. when max=3 the list.size()=4
        return true;
    }
    for (int i=0;i<n;i++) {
        //直接生成下一个
        int next=last^(1<<i); //这一步其实就是从后往前，依次改变 last 一位
        if (!visit[next]) {
            lis.add(next);
            visit[next]=true;
            if(grayCode2(n,lis,visit,next)){
                return true;
            }
            lis.remove(lis.size()-1);
            visit[next]=false;
        }
    }
    return false;
}

解法三

不停的和自己右移一位的值做异或，最终就可以的到完整的格雷码，至于原理并不想去研究😂，先记住再说

//最优解，规律
public List<Integer> grayCode(int n) {
    List<Integer> res=new ArrayList<>();
    for (int i=0;i<1<<n;i++) {
        res.add(i^(i>>1));
    }
    return res;
}

看了评论区发现还有个规律，每一层的格雷码都是上一层前面加 0 和逆序上一层在前面加 1，感觉可能和上面的规律是一样的，一图以蔽之

526. 优美的排列

假设有从 1 到 N 的 N 个整数，如果从这 N 个数字中成功构造出一个数组，使得数组的第 i 位 (1 <= i <= N) 满足如下两个条件中的一个，我们就称这个数组为一个优美的排列。条件：

第 i 位的数字能被 i 整除
i 能被第 i 位上的数字整除

现在给定一个整数 N，请问可以构造多少个优美的排列？

解法一

回溯法

public int countArrangement(int N) {
    boolean[] visit=new boolean[N+1];
    return countArrangement(N,visit,1);
}

public int countArrangement(int N,boolean[] visit,int index) {
    if (index > N) {
        return 1;
    }
    int res=0;
    for (int i=1;i<=N;i++) {
        if (!visit[i] && (index%i==0 || i%index==0)) {
            visit[i]=true;
            res+=countArrangement(N,visit,index+1);
            visit[i]=false;
        }
    }
    return res;
}

其实我是想改成记忆化递归的，不然我也不会这样写，但是后面改的时候居然出了 bug，这也算是打醒了我，我一直以为这样的回溯都能改成记忆化递归。这里很明显无法做记忆化，因为你每次回溯的时候 index 相同，但是 visit 数组的状态是不一样的，直接记忆化肯定就错了。但是说到这里我发现上面的 357. 各个位数不同数字个数居然这样过了，并且还真的提高了效率。

784. 字母大小写全排列

给定一个字符串 S，通过将字符串 S 中的每个字母转变大小写，我们可以获得一个新的字符串。返回所有可能得到的字符串集合。

示例：

输入：S = "a1b2"
输出：["a1b2", "a1B2", "A1b2", "A1B2"]

输入：S = "3z4"
输出：["3z4", "3Z4"]

输入：S = "12345"
输出：["12345"]

注意：

S 的长度不超过 12。
S 仅由数字和字母组成。

解法一

一看是简单题，屁颠屁颠就开始搞，结果发现没想象中简单（主要是我太菜了）

private List<String> res=new ArrayList<>();

public List<String> letterCasePermutation(String S) {
    letterCasePermutation(S,0,new StringBuilder(S));
    return res;
}

public void letterCasePermutation(String S,int index,StringBuilder cur) {
    res.add(cur.toString()); //变化一次就添加一次
    for (int i=index;i<S.length();i++) {
        char c=S.charAt(i);
        if (c>='0' && c<='9') {
            continue;
        }
        cur.replace(i,i+1,letterCase(c));
        letterCasePermutation(S,i+1,cur);
        cur.replace(i,i+1,letterCase(cur.charAt(i))); //状态重置
    }
}

//这里其实有一个小技巧：c^(1<<5) 就可以使大写变小写，小写变大写
public String letterCase(char c){
    if (c>='a' && c<='z') { //65:A 97:a
        c-=32;
    }else if (c>='A' && c<='Z') {
        c+=32;
    }
    return c+"";
}

这里的状态重置和之前的不太一样，不过整体还是很好想的，其实也可以完全不用循环的形式

1079. 活字印刷

你有一套活字字模 tiles，其中每个字模上都刻有一个字母 tiles[i]。返回你可以印出的非空字母序列的数目。

示例 1：

输入："AAB"
输出：8
解释：可能的序列为 "A", "B", "AA", "AB", "BA", "AAB", "ABA", "BAA"。

示例 2：

输入："AAABBC"
输出：188

提示：

1 <= tiles.length <= 7
tiles 由大写英文字母组成

解法一

这道题还是挺有意思的，有点结合全排列和子集的意思，

public int numTilePossibilities(String tiles) {
    boolean[] visit=new boolean[tiles.length()];
    char[] cs=tiles.toCharArray();
    Arrays.sort(cs);
    numTilePossibilities(cs,visit);
    return count;
}

int count=-1;

//排序去重
public void numTilePossibilities(char[]cs,boolean[] visit) {
    count++;
    for (int i=0;i<cs.length;i++) {
        //想清楚这里为啥必须是！visit[i-1]
        if(i>0 && cs[i]==cs[i-1] && !visit[i-1]){ 
            continue;
        }
        if (!visit[i]) {
            visit[i]=true;
            numTilePossibilities(cs,visit);
            visit[i]=false;
        }
    }
}

这题收获比较大，对排列组合类型的题目又多了一层理解，同时也纠正了之前的错误观点

Bug 警告！！！

看一下最开始写的错误解法，唯一的区别就在这个!visit[i-1]上！

 if (i>0 && cs[i]==cs[i-1] && visit[i-1])

这里我之前一直理解成了保留第一个分支，上一个元素已经访问过了，后面就直接跳过，做了这一题写出问题了才知道原来这里完全理解反了😂，当时没有仔细想，其实这里细想一下就很容易发现问题，visit 数组其实保证的是当前这一条自上而下的纵向分支内不会有重复位置的元素被选取，而这里我们要确保的其实是横向的不重复，也就是同一层内不重复，所以这里使用visit[i-1] 其实从语义上来说就是有问题的，画个图来说明下为啥会有问题

画个递归树，然后模拟一下，其实就明白了，使用visit[i-1]的方式，生成的第一个分支其实就不完整了，只有后面的第二个分支才会是完整的，所以可以理解为保留最后一个分支，将前面的分支剪掉，在全排列中因为有长度限制，第一个分支并没有达到给定的长度，所以并不会加入结果集，对结果没有影响，（其实是会影响效率的，会重复的遍历分支，这个打印一下生成全排列过程的结果集就能看出来）

但是在这一题，并没有长度的限制，所以 count 会将第一个不完整的分支也当作结果集算进去，而后面第二个分支的时候（完整分支）又会计算一遍，结果就错了

那为什么!visit[i-1] 就可以呢？

其实也很好理解，visit 虽然保证的是纵向的不重复，但是每遍历完一个分支后，都会回溯状态，而我们又是按照顺序来遍历元素的，所以如果上一个元素的 visit[i] 是 false，那就说明上一个元素的分支已经遍历完了！以它开头的所有排列都找完了，这个时候我们判断是否相等然后跳过，才是真正的保留了第一个分支！后面的直接跳过，减少了多余的操作，同时也不会出现 bug，所以你明白以后要用那个了吧😉

1291. 顺次数

我们定义「顺次数」为：每一位上的数字都比前一位上的数字大 1 的整数。

请你返回由 [low, high] 范围内所有顺次数组成的有序列表（从小到大排序）。

示例 1：

输出：low = 100, high = 300
输出：[123,234]

示例 2：

输出：low = 1000, high = 13000
输出：[1234,2345,3456,4567,5678,6789,12345]

提示：

10 <= low <= high <= 10^9

解法一

回溯 tag 下的，某一次周赛的题，我写的已经不像回溯了，尾递归，有点鸡肋

public List<Integer> sequentialDigits(int low, int high) {
    String slow=String.valueOf(low);
    int slen=slow.length();
    int first=Integer.valueOf(slow.charAt(0))-'0'-1;
    List<Integer> res=new ArrayList<>();
    int start=first,len=slen;
    if(first+len>9){
        start=0;
        len++;
    }
    sequentialDigits(low,high,start,len,res);
    return res;
}

private String str="123456789";

public void sequentialDigits(int low,int high,int start,int len,List<Integer> list) {
    if(start+len>9) return;
    int cur=Integer.valueOf(str.substring(start,start+len));
    if(cur>high){
        return;
    }
    if(cur>=low){
        list.add(cur);
    }
    if(start+len==9){
        sequentialDigits(low,high,0,len+1,list);    
    }else{
        sequentialDigits(low,high,start+1,len,list);
    }
}

其实直接暴力枚举1~9的所有顺序组合然后判断在不在low~high 之间就 ok 了，最再排个序就 ok，一共也只有 36 个，个人感觉我上面的还是比单纯的暴力会好一点，首先不用排序，其次也不会从头开始遍历，会根据 low 的值来选取从哪里开始截取，但是这题数据量有限，体现不出来差异

22. 括号生成

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：

[
  "((()))",
  "(()())",
  "(())()",
  "()(())",
  "()()()"
]

解法一

哎，知道是回溯还是没做出来，还是太菜了啊

public List<String> generateParenthesis(int n) {
    dfs(n,"",0,0);
    return res;
}

private List<String> res=new LinkedList<>();

public void dfs(int n,String sb,int left,int right) {
    if (left>n /*|| right>n*/ || right>left) {
        return;
    }
    if (left==n && right ==n) {
        res.add(sb.toString());   
        return;
    }
    dfs(n,sb+"(",left+1,right);
    dfs(n,sb+")",left,right+1);
}

关键还是没想明白这题的递归条件，我知道是先生成 “(“ 再生成 “)” 但是终止条件一直没想清楚，其实我们需要给左右括号加一个计数器left 和 right，用来记录已经生成的左右括号的数量，然后我们思考终止条件是啥，首先很容易想到的就是左右括号数量 left==right 的时候，这是合法的终止条件，但是这样就够了么？很明显不够，()))(( 类似这样的就并不是合法的，所以我们还需要保证生成括号的合法性，所以这种时候若是不太清楚的就可以来画一画递归树

图画的比较魔性，但是还是很容易看懂的，通过这个递归树我还发现了上面代码的一点小问题，right>n 是个冗余条件，合法条件 right< left < n，right 肯定不会超过 n，正如上面三个画 ❌的地方就是对应的三个不合法的终止条件，有了这个就可以很容易的写出回溯代码，下面的是用的StringBuilder的，需要回溯字符串，更符合回溯的思想，上面的 String 是不可变对象，所以不需要手动回溯

public List<String> generateParenthesis(int n) {
    dfs(n,new StringBuilder(),0,0);
    return res;
}

private List<String> res=new LinkedList<>();

public void dfs(int n,StringBuilder sb,int left,int right) {
    if (left>n || right>n || right>left) {
        return;
    }
    if (left==n && right ==n) {
        res.add(sb.toString());
        return;
    }
    dfs(n,sb.append("("),left+1,right);
    sb.delete(sb.length()-1,sb.length());
    dfs(n,sb.append(")"),left,right+1);
    sb.delete(sb.length()-1,sb.length());
}

306. 累加数

累加数是一个字符串，组成它的数字可以形成累加序列。

一个有效的累加序列必须至少包含 3 个数。除了最开始的两个数以外，字符串中的其他数都等于它之前两个数相加的和。

给定一个只包含数字 '0'-'9' 的字符串，编写一个算法来判断给定输入是否是累加数。

说明： 累加序列里的数不会以 0 开头，所以不会出现 1, 2, 03 或者 1, 02, 3 的情况。

示例 1:

输入："112358"
输出：true 
解释：累加序列为：1, 1, 2, 3, 5, 8 。1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5, 3 + 5 = 8

示例 2:

输入："199100199"
输出：true 
解释：累加序列为：1, 99, 100, 199。1 + 99 = 100, 99 + 100 = 199

进阶：

你如何处理一个溢出的过大的整数输入？

解法一

在回溯专题里翻到的，说实话，case 有点恶心

public boolean isAdditiveNumber(String num) {
    LinkedList<String> list=new LinkedList<>();
    list.add("-1");
    return dfs(num,0,list);
}

public boolean dfs(String num,int index,List<String> list) {
    //System.out.println(list);
    if (index==num.length() && list.size()>4) {
        return true;
    }
    for(int i=index+1;i<=num.length();i++){
        //0 开头应该直接 break, 除非是单独的 0....
        if (num.charAt(index)=='0' && i>index+1) { //"101" .....
            break;
        }
        //剪枝
        if (i-index>num.length()/2) {
            return false;
        }
        String sub=num.substring(index,i);
        String a=list.get(list.size()-1);
        String b=list.get(list.size()-2);
        list.add(sub);
        if (("-1".equals(a)||"-1".equals(b) || addTwoStr(a,b).equals(sub)) && dfs(num,i,list)) {
            return true;
        }
        list.remove(list.size()-1);
    }
    return false;
}

//大数相加
private String addTwoStr(String a,String b){
    StringBuilder res=new StringBuilder();
    int aIdx=a.length()-1;
    int bIdx=b.length()-1;
    int temp=0; //进位
    while(aIdx>=0 || bIdx>=0) {
        int as=aIdx>=0?a.charAt(aIdx)-48:0;
        int bs=bIdx>=0?b.charAt(bIdx)-48:0;
        int sum=as+bs+temp;
        temp=(sum)/10;
        res.append(sum%10);
        aIdx--;bIdx--;
    }
    if (temp==1) {
        res.append(1);
    }
    return res.reverse().toString();
}

回溯不难想到，这一类回溯咋说呢，属于 “一镜到底” 的那种，可以看看解数独的哪个解法，也是这样的（其实就是参考的那个）带一个 boolean 返回值，走到结尾走不通才会回溯，N 皇后这种就不太一样，不管是否成功都会回溯，反正目前大致的感觉就是这样，后面遇到更多题型再来总结

不过感觉这题的关键不是回溯，而是边界的处理，首先是溢出的问题，我看见有进阶的就没考虑溢出，结果还是溢出了，而且溢出了两次！！！最后没办法，也不想用BigInteger就自己写了大数相加的逻辑

除了溢出的问题，这题需要注意 0 在这个0 上也 WA 了一发，因为回溯还是在分割字符串，但是如果有 0 的话就不能随便的分割了，具体看代码就懂了

842. 将数组拆分成斐波那契序列

给定一个数字字符串 S，比如 S = “123456579”，我们可以将它分成斐波那契式的序列 [123, 456, 579]。

形式上，斐波那契式序列是一个非负整数列表 F，且满足：

0 <= F[i] <= 2^31 - 1，（也就是说，每个整数都符合 32 位有符号整数类型）；
F.length >= 3；
对于所有的 0 <= i < F.length - 2，都有 F[i] + F[i+1] = F[i+2] 成立。

另外，请注意，将字符串拆分成小块时，每个块的数字一定不要以零开头，除非这个块是数字 0 本身。

返回从 S 拆分出来的所有斐波那契式的序列块，如果不能拆分则返回 []。

示例 1：

输入："123456579"
输出：[123,456,579]

示例 2：

输入："11235813"
输出：[1,1,2,3,5,8,13]

示例 3：

输入："112358130"
输出：[]
解释：这项任务无法完成。

示例 4：

输入："0123"
输出：[]
解释：每个块的数字不能以零开头，因此 "01"，"2"，"3" 不是有效答案。

示例 5：

输入："1101111"
输出：[110, 1, 111]
解释：输出 [11,0,11,11] 也同样被接受。

提示：

1 <= S.length <= 200
字符串 S 中只含有数字。

解法一

和上面那题一样，但是这题会简单一点，不用处理大数相加的情况，同时限定了数字的范围就是 32 位 int，所以只要范围超过了 int32 就直接 break

public List<Integer> splitIntoFibonacci(String S) {
    LinkedList<Integer> res=new LinkedList<>();
    dfs(S,0,res);
    return res;
}

public boolean dfs(String S,int index,List<Integer> lis){
    if (index == S.length()) {
        return lis.size()>2;
    }
    for (int i=index+1;i<=S.length();i++) {
        String temp=S.substring(index,i);
        //长度大于 10, 或者 Long 解析出来大于 INT_MAX 了就直接 break
        if (S.charAt(index) == '0' && i>index+1 || temp.length()>10 || Long.valueOf(temp)>Integer.MAX_VALUE) {
            break;
        }
        int str=Integer.valueOf(temp);
        int one=lis.size()>=2 ? lis.get(lis.size()-1):-1;
        int two=lis.size()>=2 ? lis.get(lis.size()-2):-1;
        lis.add(str);
        if ((one==-1 || two==-1 || one+two==str) && dfs(S,i,lis)) {
            return true;
        }
        lis.remove(lis.size()-1);
    }
    return false;
}

139. 单词拆分

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，判定 s 是否可以被空格拆分为一个或多个在字典中出现的单词。

说明：

拆分时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。

示例 1：

输入：s = "leetcode", wordDict = ["leet", "code"]
输出：true
解释：返回 true 因为 "leetcode" 可以被拆分成 "leet code"。

示例 2：

输入：s = "applepenapple", wordDict = ["apple", "pen"]
输出：true
解释：返回 true 因为 "applepenapple" 可以被拆分成 "apple pen apple"。
     注意你可以重复使用字典中的单词。

示例 3：

输入：s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
输出：false

解法一

回溯 DFS+记忆化

Boolean[] cache=null;

public boolean wordBreak(String s, List<String> wordDict) {
    if (s==null || s.length()<=0) {
        return false;
    }
    cache=new Boolean[s.length()];
    HashSet<String> set=new HashSet<>(wordDict);
    return dfs(s,set,0);
}

//判断【index,s.len】中的字符是否能拆分
public boolean dfs(String s, HashSet<String> dict,int index) {
    //这里的终止条件还是有点迷惑的，这里 index 只有在字典中存在当前元素的时候才会向后移动
    //所以当 index 移动到 s==length 的是偶就说明前面的单词都匹配上了
    if (index==s.length()) {
        return true;
    }
    if (cache[index]!=null) {
        return cache[index];
    }
    for (int i=index+1;i<=s.length();i++) {
        //System.out.println(s.substring(index,i));
        if (dict.contains(s.substring(index,i)) && dfs(s,dict,i)){
            return cache[index]=true;
        }
    }
    return cache[index]=false;
}

很久之前做的题目，在做这题进阶版的时候发现这一题做了但是没有记录。可能是忘了

这里回溯记忆化没啥好说的，也是属于那种 “一镜到底” 类型的

解法二

BFS

//BFS, 需要一个 visit 保证不会重复访问
public boolean wordBreak(String s, List<String> wordDict) {
    if (s==null || s.length()<=0) {
        return false;
    }
    HashSet<String> dict=new HashSet<>(wordDict);
    //queue 中存 index
    LinkedList<Integer> queue=new LinkedList<>();
    boolean[] visit=new boolean[s.length()];
    queue.add(0);
    while(!queue.isEmpty()){
        int index=queue.poll();
        if (!visit[index]) {
            for (int i=index+1;i<=s.length();i++) {
                if(dict.contains(s.substring(index,i))){
                    if (i==s.length()) {
                        return true;
                    }
                    queue.add(i);
                }
            }
            visit[index]=true;
        }
    }
    return false;
}

自己写的居然一点印象都没有，BFS 感觉也没啥好说的

解法三

动态规划，这个当时没有写出来，今天重新看的时候发现有 dp 的 tag 就写了一下，还是挺简单的

public boolean wordBreak(String s, List<String> wordDict) {
    if (s==null || s.length()<=0) {
        return false;
    }
    HashSet<String> dict=new HashSet<>(wordDict);
    boolean[] dp=new boolean[s.length()+1];
    dp[0]=true;
    for (int i=1;i<=s.length();i++) {
        for (int j=0;j<=i;j++) {
            if (dp[j] && dict.contains(s.substring(j,i))) {
               dp[i]=true; //相比上面的可以 break
               break;
            }
        }
    }
    return dp[s.length()];
}

140. 单词拆分 II

给定一个非空字符串 s 和一个包含非空单词列表的字典 wordDict，在字符串中增加空格来构建一个句子，使得句子中所有的单词都在词典中。返回所有这些可能的句子。

说明：

分隔时可以重复使用字典中的单词。
你可以假设字典中没有重复的单词。

示例 1：

输入：
s = "catsanddog"
wordDict = ["cat", "cats", "and", "sand", "dog"]
输出：
[
  "cats and dog",
  "cat sand dog"
]

示例 2：

输入：
s = "pineapplepenapple"
wordDict = ["apple", "pen", "applepen", "pine", "pineapple"]
输出：
[
  "pine apple pen apple",
  "pineapple pen apple",
  "pine applepen apple"
]
解释：注意你可以重复使用字典中的单词。

示例 3：

输入：
s = "catsandog"
wordDict = ["cats", "dog", "sand", "and", "cat"]
输出：
[]

解法一

这题要求出所有的序列，所以 dp 肯定是不好整了，直接上回溯

public List<String> wordBreak(String s, List<String> wordDict) {
    HashSet<String> dict=new HashSet<>(wordDict);
    dfs(s,0,"",dict);
    return res;
}

private List<String> res=new ArrayList<>();

public void dfs(String s,int index,String word,HashSet<String> dict){
    if (index==s.length()) {
        res.add(word.substring(0,word.length()-1));
        return;
    }
    for (int i=index+1;i<=s.length();i++) {
        String str=s.substring(index,i);
        if (dict.contains(str)) {
            //word.append(str+" "); // app#pa# 
            dfs(s,i,word+str+" ",dict);
            //word.delete(word.length()-(i-),i);
        }
    }
}

很可惜，超时了，卡在了 aaaaaaaa…. 那个 case 上，翻了评论区，发现很多人借用了上一题的解法，先对整个 s 做可行性分析，也就是看能不能拆分，能拆分然后再进行回溯，这样就刚好跳过了那个 case，好像确实是可以过，但是我感觉有点面向 case 编程了。

解法二

记忆化回溯，上面的过程分析一下会发现其实有很多的重复计算，所以我们可以有针对性的做记忆化，加快搜索速度

//做记忆化
HashMap<String,List<String>> cache=new HashMap<>();

public List<String> wordBreak(String s, List<String> wordDict) {
    HashSet<String> dict=new HashSet<>(wordDict);
    return dfs(s,dict);
}

public List<String> dfs(String s,HashSet<String> dict){
    if (cache.containsKey(s)) {
        return cache.get(s);
    }
    List<String> res=new ArrayList<>();
    if (s.length()==0) {
        return res;
    }
    for (int i=0;i<=s.length();i++) {
        String word=s.substring(0,i);
        if (dict.contains(word)) {
            if (i==s.length()) {
                res.add(word);
            }else{
                //剩余字符
                List<String> temp=dfs(s.substring(i,s.length()),dict);
                for (String tmp:temp) {
                    res.add(word+" "+tmp);
                }
            }
        }
    }
    cache.put(s,res);
    return res;
}

其实我这里也是参考了评论区的解法，我上面的那种回溯的方式要改成记忆化有点不好搞，有两个变量，另外我感觉这种回溯分割的方式感觉更加的直观易懂 get

UPDATE: 2020.7.8

偶然看到这个题，重写了一下，直接记忆化

//记忆化递归
func wordBreak(s string, wordDict []string) []string {
    var set = make(map[string]bool)
    var cache = make(map[string][]string)
    for i := 0; i < len(wordDict); i++ {
        set[wordDict[i]] = true
    }
    return dfs(s, set, cache)
}

func dfs(s string, set map[string]bool, cache map[string][]string) []string {
    if _, ok := cache[s]; ok {
        return cache[s]
    }
    var res []string
    for i := 1; i <= len(s); i++ {
        if set[s[:i]] {
            if i == len(s) {
                res = append(res, s[:i])
            } else {
                temp := dfs(s[i:], set, cache)
                for _, w := range temp {
                    res = append(res, s[:i]+" "+w)
                }
            }
        }
    }
    cache[s] = res
    return res
}

473. 火柴拼正方形

还记得童话《卖火柴的小女孩》吗？现在，你知道小女孩有多少根火柴，请找出一种能使用所有火柴拼成一个正方形的方法。不能折断火柴，可以把火柴连接起来，并且每根火柴都要用到。

输入为小女孩拥有火柴的数目，每根火柴用其长度表示。输出即为是否能用所有的火柴拼成正方形。

示例 1:

输入：[1,1,2,2,2]
输出：true

解释：能拼成一个边长为 2 的正方形，每边两根火柴。

示例 2:

输入：[3,3,3,3,4]
输出：false

解释：不能用所有火柴拼成一个正方形。

注意：

给定的火柴长度和在 0 到 10^9之间。
火柴数组的长度不超过 15。

解法一

//等价于能否将 nums 分为 4 等分
public boolean makesquare(int[] nums) {
    if(nums==null || nums.length<4){
        return false;
    }
    int N=nums.length;
    int sum=0;
    for(int i=0;i<N;i++){
        sum+=nums[i];
    }
    if(sum%4!=0) return false;
    int[] side=new int[4];
    Arrays.sort(nums);
    return dfs(nums,N-1,side,sum/4);
}

public boolean dfs(int[] nums,int index,int[] side,int avg){
    if(index==-1){
        return true;
    }
    for(int i=0;i<side.length;i++){
        //if(side[i]+nums[index]<=avg){
        int rest=avg-side[i]-nums[index];
        if(rest==0 || rest>=nums[0]){ //改进剪枝方式
            side[i]+=nums[index];
            if(dfs(nums,index-1,side,avg)){
                return true;
            }
            side[i]-=nums[index];
        }
    }
    return false;
}

一开始没想到分桶的做法，只想着这么搜索 4 等分，看了一眼评论区就明白了，抽象出 4 条边，然后遍历所有火柴，尝试将火柴放入所有的盒子，看有没有一种可能是 4 等分的，说白了其实就是暴力搜索，然后加上一点剪枝优化，这题就不细说了，关键看下面这题

698. 划分为 k 个相等的子集

给定一个整数数组 nums 和一个正整数 k，找出是否有可能把这个数组分成 k 个非空子集，其总和都相等。

示例 1：

输入： nums = [4, 3, 2, 3, 5, 2, 1], k = 4
输出： True
说明： 有可能将其分成 4 个子集（5），（1,4），（2,3），（2,3）等于总和。

注意：

1 <= k <= len(nums) <= 16
0 < nums[i] < 10000

解法一

473. 火柴拼正方形其实只是这道题的一个子问题，关键搞懂这题就行了

public boolean canPartitionKSubsets(int[] nums, int k) {
    if(nums==null || nums.length<=0){
        return false;
    }
    int sum=0;
    for(int i=0;i<nums.length;i++){
        sum+=nums[i];
    }
    if(sum%k!=0) return false;
    Arrays.sort(nums);
    return dfs(nums,nums.length-1,new int[k],sum);
}

public boolean dfs(int[] nums,int index,int[] bucket,int sum){
    //sum(bucket)==sum
    //if 条件：bucket[i]<=sum/bucket.len => bucket[i]<=sum(bucket)/bucket.len
    //所以不用单独去判断是否都相等，直接 retuen true
    if(index==-1){
        return true;
    }
    for(int i=0;i<bucket.length;i++){
        //普通的剪枝 60ms，只判断了是否小于平均值
        //if(bucket[i]+nums[index]<=sum/bucket.length){
        //更好的剪枝方式 1ms，判断剩余空间不为 0 的时候还能不能填其他元素
        int rest=sum/bucket.length-bucket[i]-nums[index];
        if(rest==0 || rest>=nums[0]){ //小于 nums[0] 就啥也填不了了
            bucket[i]+=nums[index];
            if(dfs(nums,index-1,bucket,sum)){
                return true;
            }
            bucket[i]-=nums[index];
        }
    }
    return false;
}

其实总体上来说还是暴力的搜索，然后加上一些剪枝优化的手段，首先能想到的是约束桶内元素和要小于等于sum/k，这样就能减去很多无效搜索，但是仅仅这样还是无法 AC 这题，还有一步很关键的优化点是排序，排序后我们从大往小搜索，也就是优先将大的元素放入桶中，尽快满足 if 条件，经过上面的优化就可以成功的 AC 了，耗时 60ms 左右，但是看了评论区的大佬的解法后发现还有一种更好的剪枝方式，就是考虑放下当前元素后还能不能放下其他的元素，如果刚好放下就直接放，如果放下后还有剩余空间，且这个剩余空间很小，连nums[0]都放不下（前面排序了）那么这种情况也是可以直接剪掉的，时间优化到 1ms

index==-1为什么就直接返回 true 了？简单推一下就行了

首先index==-1说明所有元素都已经放入bucket中了，所以sum(bucket)=sum(nums)

再来看我们的 if 条件：约束桶内元素小于等于sum/k，也就是bucket[i]<=sum(nums)/k 借助上面的结论，转换一下就是 bucket[i]<=sum(bucket)/k也就是bucket[i]<=avg(bucket)很明显，只有在每个桶内元素都相等的时候才成立，故这里可以直接返回 true

解法二

官方提供了一个状压的方法，但是没看懂，自己试着压了下没过，懒得去研究了

491. 递增子序列

Difficulty: 中等

给定一个整型数组，你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是 2。

示例：

输入：[4, 6, 7, 7]
输出：[[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]

说明：

给定数组的长度不会超过 15。
数组中的整数范围是 [-100,100]。
给定数组中可能包含重复数字，相等的数字应该被视为递增的一种情况。

解法一

感觉今天晚上状态不太好，好久没写回溯了，写了几发思路都有问题，最后瞄了一眼评论区才反应过来，和上面 842-将数组拆分成斐波那契序列很类似，都是利用 lis 数组上次存值判断，当时这题还是我独立写出来的，写完发的 code 评论还是个热评，今天写这题居然没反应过来，太菜了😥

func findSubsequences(nums []int) [][]int {
    var n = len(nums)
    var res [][]int
    var dfs func(int, []int)
    dfs = func(index int, lis []int){
        if len(lis) >= 2{
            dest := make([]int, len(lis))
            copy(dest, lis)
            res = append(res, dest)
        }
        //保证一次 for 循环中没有重复的就行了，根据取值范围做下偏移
        var visit = make([]bool, 201)
        for i := index; i < n; i++{
            if !visit[nums[i]+100] && (len(lis) == 0 || nums[i] >= lis[len(lis)-1]) {
                visit[nums[i]+100] = true
                lis = append(lis, nums[i])
                dfs(i+1, lis)
                lis = lis[:len(lis)-1]
            }
        }
    }
    dfs(0, make([]int, 0))
    return res
}

679. 24 点游戏

Difficulty: 困难

你有 4 张写有 1 到 9 数字的牌。你需要判断是否能通过 *，/，+，-，(，) 的运算得到 24。

示例 1:

输入：[4, 1, 8, 7]
输出：True
解释：(8-4) * (7-1) = 24

示例 2:

输入：[1, 2, 1, 2]
输出：False

注意：

除法运算符 / 表示实数除法，而不是整数除法。例如 4 / (1 - 2/3) = 12 。
每个运算符对两个数进行运算。特别是我们不能用 - 作为一元运算符。例如，[1, 1, 1, 1] 作为输入时，表达式 -1 - 1 - 1 - 1 是不允许的。
你不能将数字连接在一起。例如，输入为 [1, 2, 1, 2] 时，不能写成 12 + 12 。

解法一

代码有点长，不过思路还是很清楚，一共 4 个数字，从里面任意选 2 个，然后做各种运算后和剩下的数字构成新的数组，然后重复该过程直到数组只剩下一个然后判断值是否是 24（注意精度）

func judgePoint24(nums []int) bool {
    var eps float32 = 1e-5
    var Abs = func(a float32) float32 {
        if a < 0 {
            return -a
        }
        return a
    }
    //计数+-*/
    var compute = func(a, b float32) []float32 {
        return []float32{a + b, a * b, a - b, a / b}
    }
    var dfs func([]float32) bool
    dfs = func(nums []float32) bool {
        if len(nums) == 0 {
            return false
        }
        if len(nums) == 1 {
            return Abs(nums[0]-24) < eps
        }
        var n = len(nums)
        //从 nums 中选取 2 个数
        for i := 0; i < n; i++ {
            for j := 0; j < n; j++ {
                if i == j {
                    continue
                }
                //收集剩下的数字
                var rest []float32
                for k := 0; k < n; k++ {
                    if k != i && k != j {
                        rest = append(rest, nums[k])
                    }
                }
                //尝试做各种运算
                for _, v := range compute(nums[i], nums[j]) {
                    if dfs(append(rest, v)) {
                        return true
                    }
                }
            }
        }
        return false
    }
    var temp = make([]float32, len(nums))
    for i := 0; i < len(nums); i++ {
        temp[i] = float32(nums[i])
    }
    return dfs(temp)
}

5526. 最多可达成的换楼请求数目

Difficulty: 困难

我们有 n 栋楼，编号从 0 到 n - 1 。每栋楼有若干员工。由于现在是换楼的季节，部分员工想要换一栋楼居住。

给你一个数组 requests ，其中 requests[i] = [from_i, to_i] ，表示一个员工请求从编号为 from_i 的楼搬到编号为 to_i的楼。

一开始 所有楼都是满的，所以从请求列表中选出的若干个请求是可行的需要满足每栋楼员工净变化为 0 。意思是每栋楼离开的员工数目等于该楼搬入的员工数数目。比方说 n = 3 且两个员工要离开楼 0 ，一个员工要离开楼 1 ，一个员工要离开楼 2 ，如果该请求列表可行，应该要有两个员工搬入楼 0 ，一个员工搬入楼 1 ，一个员工搬入楼 2 。

请你从原请求列表中选出若干个请求，使得它们是一个可行的请求列表，并返回所有可行列表中最大请求数目。

示例 1：

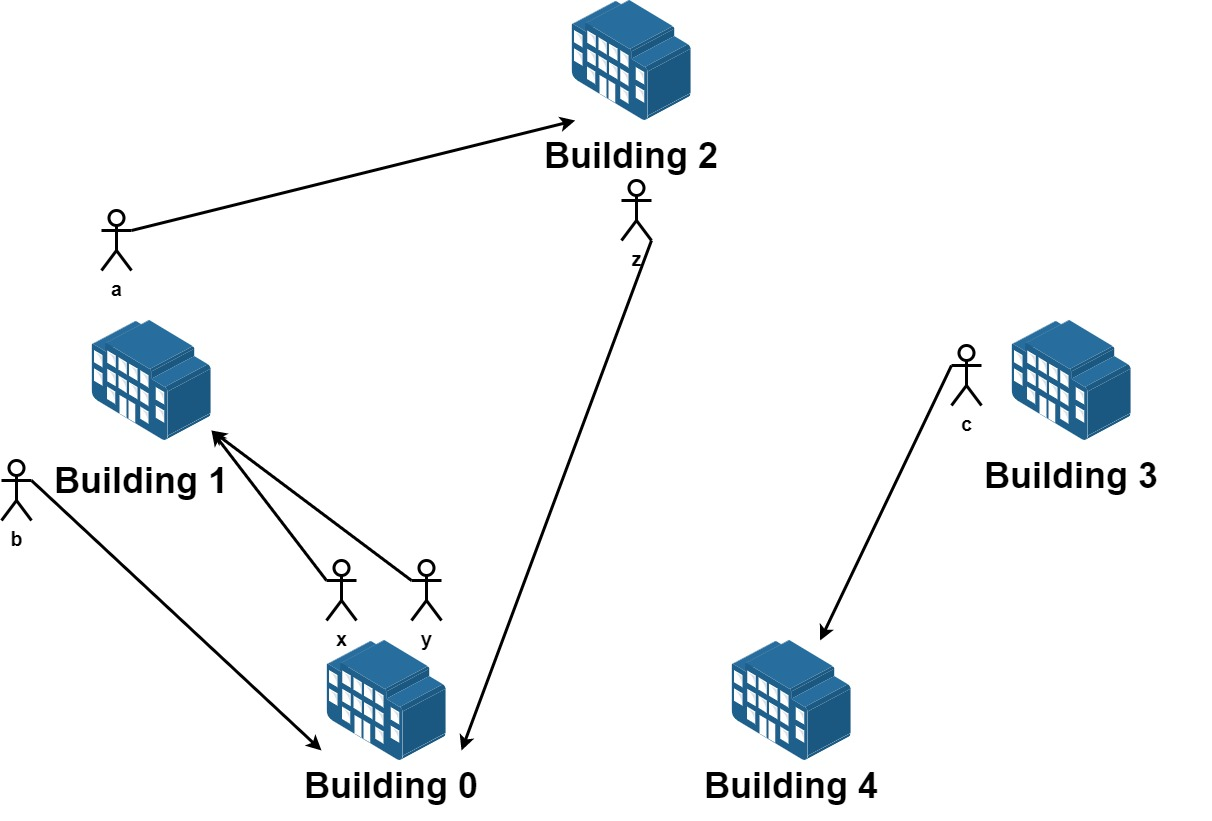
输入：n = 5, requests = [[0,1],[1,0],[0,1],[1,2],[2,0],[3,4]]
输出：5
解释：请求列表如下：
从楼 0 离开的员工为 x 和 y ，且他们都想要搬到楼 1 。
从楼 1 离开的员工为 a 和 b ，且他们分别想要搬到楼 2 和 0 。
从楼 2 离开的员工为 z ，且他想要搬到楼 0 。
从楼 3 离开的员工为 c ，且他想要搬到楼 4 。
没有员工从楼 4 离开。
我们可以让 x 和 b 交换他们的楼，以满足他们的请求。
我们可以让 y，a 和 z 三人在三栋楼间交换位置，满足他们的要求。
所以最多可以满足 5 个请求。

示例 2：

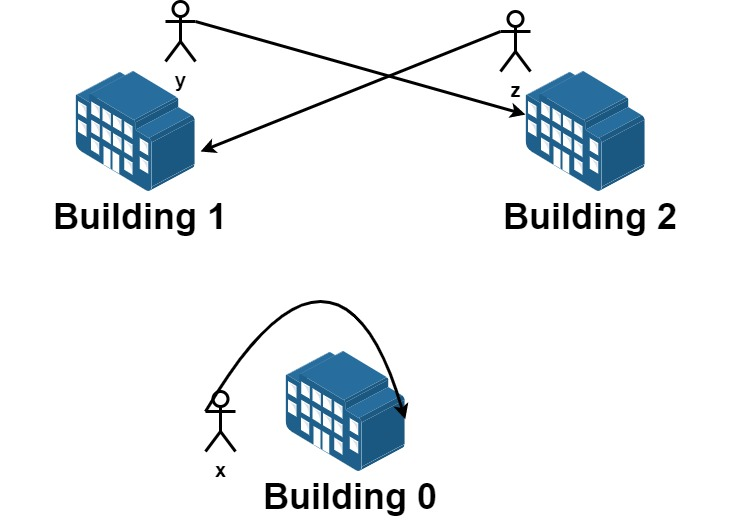
输入：n = 3, requests = [[0,0],[1,2],[2,1]]
输出：3
解释：请求列表如下：
从楼 0 离开的员工为 x ，且他想要回到原来的楼 0 。
从楼 1 离开的员工为 y ，且他想要搬到楼 2 。
从楼 2 离开的员工为 z ，且他想要搬到楼 1 。
我们可以满足所有的请求。

示例 3：

输入：n = 4, requests = [[0,3],[3,1],[1,2],[2,0]]
输出：4

提示：

1 <= n <= 20
1 <= requests.length <= 16
requests[i].length == 2
0 <= from_i, to_i < n

解法一

208 周赛 T4，有点白给，想好怎么处理就很简单（好不容易 T4 这么简单，被 T2，T3 给干懵了）

class Solution {
    public int maximumRequests(int n, int[][] requests) {
        int[] nums = new int[n+1];
        dfs(nums, 0, requests, 0);
        return res;
    }
    
    int res = 0;
    
    public void dfs(int[] nums, int idx, int[][] requests, int count){
        if (check(nums)) {
            res = Math.max(res, count);
        }
        for (int i = idx; i < requests.length; i++) {
            nums[requests[i][0]]--;
            nums[requests[i][1]]++;
            dfs(nums, i+1, requests, count+1);
            nums[requests[i][0]]++;
            nums[requests[i][1]]--;
        }
    }
    
    public boolean check(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != 0) {
                return false;
            }
        }
        return true;
    }
}

二维平面上的回溯

79. 单词搜索

给定一个二维网格和一个单词，找出该单词是否存在于网格中。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

示例：

board =
[
  ['A','B','C','E'],
  ['S','F','C','S'],
  ['A','D','E','E']
]

给定 word = "ABCCED", 返回 true.
给定 word = "SEE", 返回 true.
给定 word = "ABCB", 返回 false.

解法一

这题其实并不难，但是我一开始就钻到死胡里去了，我直接拿起来就想的是暴力 dfs 从（0，0）开始遍历每种情况，直到找到一个相等的。我真是个 hapi

/*
    board =
    [
      ['A','B','C','E'],
      ['S','F','C','S'],
      ['A','D','E','E']
    ]
     */

//方向：右，下，左，上
private int[][] direction={{0,1},{1,0},{0,-1},{-1,0}};

public boolean exist(char[][] board, String word) {
    if (board==null || word==null) {
        return false;
    }
    char[] words=word.toCharArray();
    boolean[][] visit=new boolean[board.length][board[0].length];
    for (int i=0;i<board.length;i++) {
        for (int j=0;j<board[0].length;j++) {
            //遍历 board 每个元素，以为个元素为起点都试一下
            if(dfs(board,words,0,i,j,visit)){
                return true;
            }
        }
    }
    return false;
}

public boolean dfs(char[][] board, char[] word,int index,int x,int y,boolean[][] visit) {
    //遍历到 word 的最后一个字符了，直接比较就可以得出结果
    if (index == word.length-1) {
        return word[index] == board[x][y];
    }
    /*
     这样写如果 board 只有一个元素就会错了，后面的 isValid 会直接 false, 但是有可能 word 就是这个 board
     if (index == word.length) {
            return true;
     }*/
    
    //当元素相等的时候才有继续的必要
    if (board[x][y]==word[index]) {
        visit[x][y]=true;
        for (int i=0;i<direction.length;i++) {
            int nx=x+direction[i][0];
            int ny=y+direction[i][1];
            //保证合法性
            if (isValid(board,nx,ny)&&!visit[nx][ny]&&dfs(board,word,index+1,nx,ny,visit)) {
                return true;
            }
        }
        visit[x][y]=false;
    }
    return false;
}

public boolean isValid(char[][] cs,int x,int y){
    return x>=0 && x<cs.length && y >=0 && y< cs[0].length;
}

200. 岛屿数量

给定一个由 ‘1’（陆地）和 ‘0’（水）组成的的二维网格，计算岛屿的数量。一个岛被水包围，并且它是通过水平方向或垂直方向上相邻的陆地连接而成的。你可以假设网格的四个边均被水包围

示例 1:

示例 2:

输入：
11000
00100
00011

输出：3

解法一

和上面一题类似，很惭愧，一开始也没写出来，写了个大概，细节没有捋清楚

//方向：右，下，左，上
private int[][] direction={{0,1},{1,0},{0,-1},{-1,0}};

public int numIslands(char[][] grid) {
    if (grid==null||grid.length<=0) {
        return 0;
    }
    boolean[][] visit=new boolean[grid.length][grid[0].length];
    for (int i=0;i<grid.length;i++) {
        for (int j=0;j<grid[0].length;j++) {
            if (grid[i][j]=='1'&&!visit[i][j]) {
                dfs(grid,i,j,visit);
                res++;
            }
        }
    }
    return res;
}

private int res=0;

public void dfs(char[][] grid,int x,int y,boolean[][] visit) {
    //其实整个 dfs 做的就是对 visit[x][y] 标记，标记为 true 代表访问过
    visit[x][y]=true;
    for (int i=0;i<direction.length;i++) {
        int nx=x+direction[i][0];
        int ny=y+direction[i][1];
        if (isValid(grid,nx,ny) && !visit[nx][ny] && grid[nx][ny]=='1') {
            dfs(grid,nx,ny,visit);
            //无需回溯 visit 状态
        }
    }
}

public boolean isValid(final char[][] grid,int x,int y){
    return x>=0 && x<grid.length && y>=0 && y<grid[0].length;
}

130. 被围绕的区域

给定一个二维的矩阵，包含 'X' 和 'O'（字母 O）。

找到所有被 ‘X’ 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例：

X X X X
X O O X
X X O X
X O X X

运行你的函数后，矩阵变为：

X X X X
X O X X

解释：

被围绕的区间不会存在于边界上，换句话说，任何边界上的 ‘O’ 都不会被填充为 ‘X’。任何不在边界上，或不与边界上的 ‘O’ 相连的 ‘O’ 最终都会被填充为 ‘X’。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的

解法一

这题在很久以前（看了提交记录是一年前的）开始学 dfs 的时候，在 leetcode 搜索到了这一题，当时也做出来了，只不过效率感人，放上来看看是个啥玩意

// 定义 4 个方向（顺时针 右。..）
private static int[][] direction = { { 1, 0 }, { 0, 1 }, { -1, 0 }, { 0, -1 } };

private static int[][] mark = null;

public static void solve(char[][] board) {
    if(board.length==0) { return; }
    // 根据传进来的 board 给 mark 初始化
    mark = new int[board.length][board[0].length];
    // 遍历边缘找出边缘的 O 的坐标
    for (int i = 0; i < board.length; i++) {
        if (board[i][0] == 'O') {
            dfs(0, i, board);
            //执行完之后再赋值当前位置的 O 避免在边缘角落的问题
            mark[i][0] = 1;
        }
        if (board[i][board[0].length - 1] == 'O') {
            dfs(board[0].length, i, board);
            mark[i][board[0].length - 1] = 1;
        }
    }
    // 上边缘
    for (int i = 0; i < board[0].length; i++) {
        if (board[0][i] == 'O') {
            dfs(i, 0, board);
            mark[0][i] = 1;
        }
    }
    // 下边缘
    for (int i = 0; i < board[0].length; i++) {
        if (board[board.length - 1][i] == 'O') {
            dfs(i, board.length - 1, board);
            mark[board.length - 1][i] = 1;
        }
    }

    for (int i = 0; i < board.length; i++) {
        for (int j = 0; j < board[0].length; j++) {
            if (board[i][j] == 'O' && mark[i][j] == 0) {
                board[i][j] = 'X';
            }
        }
    }

}

// 实现函数
public static void dfs(int x, int y, char[][] board) {
    int tx, ty;
    // 首先判断边缘上有没有 O 有的话将与他联通的 O 都加上标记
    for (int i = 0; i <= 3; i++) {
        // x=x+direction[i][0]; 这样写每个点向 4 个方向扩展如果这样写 点的走向就有问题了
        tx = x + direction[i][0];
        ty = y + direction[i][1];
        // System.out.println(tx+" "+ty);
        if (tx < board[0].length && tx >= 0 && ty < board.length && ty >= 0 && board[ty][tx] == 'O'
            && mark[ty][tx] == 0) {
            // 代表走过了
            mark[ty][tx] = 1;
            // 这里没有处理好，我的 dfs 函数的参数是坐标但是对应到 mark 里面和 board 里面就不是坐标了就颠倒了
            // 比如按照坐标来 2 , 1 ---->对应到数组里面就是 1 ，2
            dfs(tx, ty, board);
        }
    }
    return;
}

21ms，8% 乍一看好像没啥问题，但是为啥这么慢呢？看看今天下午重新做的解

解法二

//方向：右，下，左，上
private int[][] direction={{0,1},{1,0},{0,-1},{-1,0}};

public void solve(char[][] board) {
    if (board==null || board.length<=0) {
        return;
    }
    boolean[][] visit=new boolean[board.length][board[0].length];
    int lx=0,ly=0;

    //遍历 4 条边的'O', 将与相连的'O'都标记为 true
    while(lx<board.length) { 
        if (board[lx][0]=='O') { //左
            dfs(board,lx,0,visit);
        }
        if (board[lx][board[0].length-1] == 'O') { //右
            dfs(board,lx,board[0].length-1,visit);
        }
        lx++;
    }

    while(ly<board[0].length) { 
        if (board[0][ly]=='O') { //上
            dfs(board,0,ly,visit);
        }
        if (board[board.length-1][ly] == 'O') { //下
            dfs(board,board.length-1,ly,visit);   
        }
        ly++;
    }

    //遍历将所有 visit=false 的 O 变为 X
    for (int i=0;i<board.length;i++) {
        for (int j=0;j<board[0].length;j++) {
            if (board[i][j]=='O' && !visit[i][j]) {
                board[i][j]='X';
            }
        }
    }
}

public void dfs(char[][] board,int x,int y,boolean[][] visit) {
    visit[x][y]=true;
    for (int i=0;i<direction.length;i++) {
        int nx=x+direction[i][0];
        int ny=y+direction[i][1];
        if (isValid(board,nx,ny) && board[nx][ny]=='O' && !visit[nx][ny]) {
            dfs(board,nx,ny,visit);
        }
    }
}

//是否合法
public boolean isValid(final char[][] grid,int x,int y){
    return x>=0 && x<grid.length && y>=0 && y<grid[0].length;
}

2ms，比较明显的区别就是 dfs 给 visit 数组赋值的时机不同，一个是在循环里面，一个是在函数开头，也就是说第一种解法并不会立即给边缘的'O' 标记，这样导致的问题就是它后续的节点仍然会搜索到这个边缘的 'O' 这样就会造成重复的计算，所以说，一定要捋清楚这个过程，不能乱写

417. 太平洋大西洋水流问题

给定一个 m x n 的非负整数矩阵来表示一片大陆上各个单元格的高度。“太平洋”处于大陆的左边界和上边界，而“大西洋”处于大陆的右边界和下边界。

规定水流只能按照上、下、左、右四个方向流动，且只能从高到低或者在同等高度上流动。

请找出那些水流既可以流动到“太平洋”，又能流动到“大西洋”的陆地单元的坐标

提示：

输出坐标的顺序不重要
m 和 n 都小于 150

示例：

给定下面的 5x5 矩阵：

  太平洋 ~   ~   ~   ~   ~ 
       ~  1   2   2   3  (5) *
       ~  3   2   3  (4) (4) *
       ~  2   4  (5)  3   1  *
       ~ (6) (7)  1   4   5  *
       ~ (5)  1   1   2   4  *
          *   *   *   *   * 大西洋

返回：

[[0, 4], [1, 3], [1, 4], [2, 2], [3, 0], [3, 1], [4, 0]] （上图中带括号的单元）.

解法一

其实和上面也是如出一辙，只不过最开始没想到两个 visit 数组来做

//方向键
private int[][] direction={{0,1},{1,0},{0,-1},{-1,0}};

public List<List<Integer>> pacificAtlantic(int[][] matrix) {
    List<List<Integer>> res=new ArrayList<>();
    //leetcode 老是喜欢搞些幺蛾子
    if (matrix==null || matrix.length<=0) {
        return res;
    }
    int m=matrix.length;
    int n=matrix[0].length;
    //太平洋
    boolean[][] pacific=new boolean[m][n];
    //大西洋
    boolean[][] atlantic=new boolean[m][n];

    for (int i=0;i<m;i++) {
        dfs(matrix,i,0,pacific);
        dfs(matrix,i,n-1,atlantic);
    }

    for (int i=0;i<n;i++) {
        dfs(matrix,0,i,pacific);
        dfs(matrix,m-1,i,atlantic);
    }
    for (int i=0;i<m;i++) {
        for (int j=0;j<n;j++) {
            //同时为 true 的就是解
            if (pacific[i][j] && atlantic[i][j]) {
                res.add(Arrays.asList(i,j));
            }
        }
    }
    return res;
}

public void dfs(int[][] matrix,int x,int y,boolean[][] visit) {
    visit[x][y]=true;
    //向 4 个方向 floodfill
    for (int i=0;i<direction.length;i++) {
        int nx=x+direction[i][0];
        int ny=y+direction[i][1];
        if (isValid(matrix,nx,ny) && matrix[nx][ny]>= matrix[x][y] && !visit[nx][ny]) {
            dfs(matrix,nx,ny,visit);
        }
    }
}

public boolean isValid(final int[][] matrix,int x,int y){
    return x>=0 && x<matrix.length && y>=0 && y<matrix[0].length;
}

6ms，96%，还是比较 ok 的

51. N 皇后

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ’ . ’ 分别代表了皇后和空位。

示例：

输入：4
输出：[
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释：4 皇后问题存在两个不同的解法

解法一

Hard 题，N 皇后问题可以说是很经典的问题了，之前有看过，但是都是一脸懵逼，无从下手，这一次看了下提示还是自己给做出来了

private List<List<String>> res=new ArrayList<>();

private boolean[] col;
//private boolean[] row;
//两条对角线
private boolean[] dia1;
private boolean[] dia2;

public List<List<String>> solveNQueens(int n) {
    if (n<=0) return res;
    col=new boolean[n];
    //row=new boolean[n];
    dia1=new boolean[2*n-1];
    dia2=new boolean[2*n-1];
    dfs(n,0,new ArrayList());
    return res;
}

//dfs
public void dfs(int n,int index,List<Integer> lis) {
    if (index==n) {
        res.add(generateRes(lis));
        return;
    }
    //检测第 index 行第 i 列
    for (int i=0;i<n;i++) {
        //注意对角线的下标
        if (!col[i] && !dia1[index-i+n-1] && !dia2[i+index]) {
            col[i]=true;
            dia1[index-i+n-1]=true;
            dia2[index+i]=true;
            //尝试添加
            lis.add(i);
            dfs(n,index+1,lis);
            //回溯
            lis.remove(lis.size()-1);
            col[i]=false;
            dia1[index-i+n-1]=false;
            dia2[index+i]=false;
        }
    }
}

//根据 lis 生成解
public List<String> generateRes(List<Integer> lis){
    List<String> res=new ArrayList<>();
    for (int i=0;i<lis.size();i++) {
        int index = lis.get(i);
        StringBuilder sb=new StringBuilder();
        for (int j=0;j<lis.size();j++) {
            if (j!=index){
                sb.append(".");
            }else{
                sb.append("Q");
            }
        }
        res.add(sb.toString());
    }
    return res;
}

核心思路就是：一行行遍历，然后 dfs 尝试在每个位置放置皇后，我觉得主要的难点在于如何判断各个列，对角线是否已经有皇后，这一点需要细致的观察，有一条对角线的横纵坐标之和为常数，另一条横纵坐标之差是个常数，借此便可以唯一确定一条对角线

52. N 皇后 II

和上面一题不同的地方是这题只需要求解的个数，感觉这题才应该是Ⅰ，不用求所有的解，貌似更加简单了？

解法一

直接套用上面的代码，没啥好说的

public int totalNQueens(int n) {
    res=0;
    if (n<=0) return 0;
    col=new boolean[n];
    //row=new boolean[n];
    dia1=new boolean[2*n-1];
    dia2=new boolean[2*n-1];
    dfs(n,0,new ArrayList());
    return res;
}

private int res=0;

private boolean[] col;
private boolean[] dia1;
private boolean[] dia2;

//dfs
public void dfs(int n,int index,List<Integer> lis) {
    if (index==n) {
        res++;
        return;
    }
    //检测第 index 行第 i 列
    for (int i=0;i<n;i++) {
        if (!col[i] && !dia1[index-i+n-1] && !dia2[i+index]) {
            col[i]=true;
            dia1[index-i+n-1]=true;
            dia2[index+i]=true;
            //不用添加到 lis 中
            dfs(n,index+1,lis);
            //回溯
            col[i]=false;
            dia1[index-i+n-1]=false;
            dia2[index+i]=false;
        }
    }
}

虽然提交了也是 1ms，主要是这两题 case 都比较少，最大的 case 好像只到 11，所以差距不是很明显，我这样做肯定不是这题的最优解，这题的最优解是利用位图（bitmap）作位运算，反正我不可能写出来就是了😂 参考

37. 解数独

编写一个程序，通过已填充的空格来解决数独问题。

一个数独的解法需遵循如下规则：

数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。空白格用 '.' 表示。

一个数独

答案被标成红色。

Note:

给定的数独序列只包含数字 1-9 和字符 '.'
你可以假设给定的数独只有唯一解。
给定数独永远是 9x9 形式的。

解法一

嗯，又是一道 hard 题，自己摸了半天没做出来，看了评论区做出来的

//三个约束规则
private boolean[][] col=new boolean[9][9];
private boolean[][] row=new boolean[9][9];
private boolean[][] block=new boolean[9][9];

public void solveSudoku(char[][] board) {
    if (board==null || board.length<=0) {
        return;
    }
    for (int i=0;i<9;i++) {
        for (int j=0;j<9;j++) {
            if (board[i][j]!='.') {
                col[i][board[i][j]-48-1]=true;
                row[j][board[i][j]-48-1]=true;
                //块号为 i/3*3+j/3
                block[i/3*3+j/3][board[i][j]-48-1]=true;
            }
        }
    }
    dfs(board,0,0);
}

//private  static char[][] res=new char[9][9];

public boolean dfs(char[][] board,int i,int j) {
    //从，i,j 位置向后寻找'.', i>=9 说明全部填充完了
    while(board[i][j]!='.') {
        j++;
        if (j==9) {
            i++;
            j=0;
        }
        //over
        if (i==9) {
            return true;
        }
    }
    //System.out.println(i+","+j);
    for (int val=0;val<9;val++) {
        if (!col[i][val] && !row[j][val] && !block[i/3*3+j/3][val]) {
            col[i][val]=true;
            row[j][val]=true;
            block[i/3*3+j/3][val]=true;
            //尝试填充为 val+1
            board[i][j]=(char)(val+1+48);
            //尝试后面的'.', 这里传进去还是 i,j
            //大脑模拟下其实这个 dfs 过程也挺简单
            if(dfs(board,i,j)){//这里会尝试所有解，失败后回溯
                return true;
            }else{
                //回溯
                board[i][j]='.';
                col[i][val]=false;
                row[j][val]=false;
                block[i/3*3+j/3][val]=false;
            }
        }
    }
    return false;
}

比上面的 N 皇后要更复杂，同样也是带有约束的 dfs 回溯，我一开始写的方法主要是思路都错了，我想的和上面 n 皇后一样，一层一层的搜索最后 n==9 就结束，但是没考虑到一层其实不只有一个空位，同时还要注意回溯的时机，并不是 dfs 之后就回溯，用大脑模拟下这个递归其实就明白了，我觉得核心还是找'.'那一步，这一步确实没想到

这题有一个简单版，36. 有效的数独挺简单的，懒得做了

529. 扫雷游戏

让我们一起来玩扫雷游戏！

给定一个代表游戏板的二维字符矩阵。 ‘M’ 代表一个未挖出的地雷，‘E’ 代表一个未挖出的空方块，‘B’ 代表没有相邻（上，下，左，右，和所有 4 个对角线）地雷的已挖出的空白方块，数字（‘1’ 到 ‘8’）表示有多少地雷与这块已挖出的方块相邻，‘X’ 则表示一个已挖出的地雷。

现在给出在所有未挖出的方块中（‘M’或者’E’）的下一个点击位置（行和列索引），根据以下规则，返回相应位置被点击后对应的面板：

如果一个地雷（‘M’）被挖出，游戏就结束了- 把它改为 ‘X’。
如果一个没有相邻地雷的空方块（‘E’）被挖出，修改它为（‘B’），并且所有和其相邻的方块都应该被递归地揭露。
如果一个至少与一个地雷相邻的空方块（‘E’）被挖出，修改它为数字（‘1’到'8’），表示相邻地雷的数量。
如果在此次点击中，若无更多方块可被揭露，则返回面板。

示例一

Input: 

[['E', 'E', 'E', 'E', 'E'],
 ['E', 'E', 'M', 'E', 'E'],
 ['E', 'E', 'E', 'E', 'E'],
 ['E', 'E', 'E', 'E', 'E']]

Click : [3,0]

Output: 

[['B', '1', 'E', '1', 'B'],
 ['B', '1', 'M', '1', 'B'],
 ['B', '1', '1', '1', 'B'],
 ['B', 'B', 'B', 'B', 'B']]

Explanation:

示例二

Input: 

[['B', '1', 'E', '1', 'B'],
 ['B', '1', 'M', '1', 'B'],
 ['B', '1', '1', '1', 'B'],
 ['B', 'B', 'B', 'B', 'B']]

Click : [1,2]

Output: 

[['B', '1', 'E', '1', 'B'],
 ['B', '1', 'X', '1', 'B'],
 ['B', '1', '1', '1', 'B'],
 ['B', 'B', 'B', 'B', 'B']]

Explanation:

解法一

标准的 DFS，还是挺有意思的，向 8 个方向扩展，遇到周围有地雷的就计数并且停止，会玩扫雷就会做😉

private int[][] direction={{0,1},{1,0},{-1,1},{1,-1},{-1,0},{0,-1},{-1,-1},{1,1}};

public char[][] updateBoard(char[][] board, int[] click) {
    int x=click[0];
    int y=click[1];
    if (board[x][y]=='M') {
        board[x][y]='X';
        return board;
    }
    boolean[][] visit=new boolean[board.length][board[0].length];
    dfs(board,x,y,visit);
    return board;
}

public void dfs(char[][] board,int x,int y,boolean[][] visit){
    visit[x][y]=true;
    int count=getRoundBoom(board,x,y);
    if(count!=0){
        board[x][y]=(char)(count+'0');
        return;
    }
    board[x][y]='B';
    for (int i=0;i<8;i++) {
        int nx=x+direction[i][0];
        int ny=y+direction[i][1];
        if (isValid(board,nx,ny) && !visit[nx][ny] && board[nx][ny]!='M') {
            dfs(board,nx,ny,visit);
        }
    }
}

public int getRoundBoom(char[][] board,int x,int y){
    int count=0;
    for (int i=0;i<8;i++) {
        int nx=x+direction[i][0];
        int ny=y+direction[i][1];
        if (isValid(board,nx,ny) && board[nx][ny]=='M') {
            count++;
        }   
    }
    return count;
}

public boolean isValid(final char[][] board,int x,int y){
    return x>=0 && x<board.length && y>=0 && y<board[0].length;
}

695. 岛屿的最大面积

给定一个包含了一些 0 和 1 的非空二维数组 grid , 一个 岛屿 是由四个方向（水平或垂直）的 1 （代表土地）构成的组合。你可以假设二维矩阵的四个边缘都被水包围着。

找到给定的二维数组中最大的岛屿面积。（如果没有岛屿，则返回面积为 0)

示例 1:

[[0,0,1,0,0,0,0,1,0,0,0,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,1,1,0,1,0,0,0,0,0,0,0,0],
 [0,1,0,0,1,1,0,0,1,0,1,0,0],
 [0,1,0,0,1,1,0,0,1,1,1,0,0],
 [0,0,0,0,0,0,0,0,0,0,1,0,0],
 [0,0,0,0,0,0,0,1,1,1,0,0,0],
 [0,0,0,0,0,0,0,1,1,0,0,0,0]]

对于上面这个给定矩阵应返回 6。注意答案不应该是 11，因为岛屿只能包含水平或垂直的四个方向的 ‘1’。

示例 2:

[[0,0,0,0,0,0,0,0]]

对于上面这个给定的矩阵，返回 0

注意： 给定的矩阵 grid 的长度和宽度都不超过 50。

解法一

和上面 200 题岛屿的数量很类似，不过还是有所不同，这里要计算的是最大的面积

private int[][] direction={{0,1},{0,-1},{1,0},{-1,0}};

public int maxAreaOfIsland(int[][] grid) {
    if (grid==null || grid.length<=0) {
        return max;
    }
    boolean[][] visit=new boolean[grid.length][grid[0].length];
    for (int i=0;i<grid.length;i++) {
        for (int j=0;j<grid[0].length;j++) {
            if (grid[i][j]==1 &&!visit[i][j]) {
                int t=dfs(grid,i,j,visit);
                max=max>t?max:t;
            }
        }
    }
    return max;
}

private int max=0;

public int dfs(int[][] grid,int x,int y,boolean[][] visit) {
    int temp=1;
    visit[x][y]=true;
    for (int i=0;i<direction.length;i++) {
        int nx=x+direction[i][0];
        int ny=y+direction[i][1];
        if (isValid(grid,nx,ny) && grid[nx][ny]==1 && !visit[nx][ny]) {
            //将 4 个方向的符合条件的数量加起来
            temp+=dfs(grid,nx,ny,visit);
        }
    }
    return temp;
}

public boolean isValid(final int[][] grid,int x,int y){
    return x>=0 && x<grid.length && y>=0 && y<grid[0].length;
}

最开始直接在 dfs 函数里面用 count 计数，居然还过了 600 多个 case….. 惊了，那种做法完全是错的，说实话有点不太习惯写有返回值的递归

547. 朋友圈

班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。

给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果 M[i] [j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

示例 1:

输入：
[[1,1,0],
 [1,1,0],
 [0,0,1]]
输出：2 
说明：已知学生 0 和学生 1 互为朋友，他们在一个朋友圈。
第 2 个学生自己在一个朋友圈。所以返回 2。

示例 2:

输入：
[[1,1,0],
 [1,1,1],
 [0,1,1]]
输出：1
说明：已知学生 0 和学生 1 互为朋友，学生 1 和学生 2 互为朋友，所以学生 0 和学生 2 也是朋友，所以他们三个在一个朋友圈，返回 1。

注意：

N 在 [1,200] 的范围内。
对于所有学生，有 M[i] [i] = 1。
如果有 M[i] [j] = 1，则有 M[j] [i] = 1。

解法一

public int findCircleNum(int[][] M) {
    if (M==null || M.length<=0) {
        return 0;
    }
    boolean[] visit=new boolean[M.length];
    int count=0;
    for (int i=0;i<M.length;i++) {
        if (!visit[i]) {
            dfs(M,visit,i);
            count++;
        }
    }
    return count;
}

//一共 m.length 个人
public void dfs(int[][] M,boolean[] visit,int index) {
    //标记 index 号学生已经访问过
    visit[index]=true;
    for (int i=0;i<M.length;i++) {
        //index 和 i 是好朋友
        if (M[index][i]==1 && !visit[i]) {
            //递归标记 i 的好朋友，形成朋友圈
            dfs(M,visit,i);
        }
    }
}

这题不知道为啥，一开始题目没搞明白。去纠结那个矩阵去了，没理解好题目的意思，其实跟那个 N*N 的矩阵没啥关系，主要是 N 个人，对每个人进行 dfs 找到与他们相关的人，做好统计就 ok，和上面的 200 题也很类似

1219. 黄金矿工

你要开发一座金矿，地质勘测学家已经探明了这座金矿中的资源分布，并用大小为 m * n 的网格 grid 进行了标注。每个单元格中的整数就表示这一单元格中的黄金数量；如果该单元格是空的，那么就是 0。

为了使收益最大化，矿工需要按以下规则来开采黄金：

每当矿工进入一个单元，就会收集该单元格中的所有黄金。
矿工每次可以从当前位置向上下左右四个方向走。
每个单元格只能被开采（进入）一次。
不得开采（进入）黄金数目为 0 的单元格。
矿工可以从网格中 任意一个 有黄金的单元格出发或者是停止。

示例 1：

输入：grid = [[0,6,0],[5,8,7],[0,9,0]]
输出：24
解释：
[[0,6,0],
 [5,8,7],
 [0,9,0]]
一种收集最多黄金的路线是：9 -> 8 -> 7。

示例 2：

输入：grid = [[1,0,7],[2,0,6],[3,4,5],[0,3,0],[9,0,20]]
输出：28
解释：
[[1,0,7],
 [2,0,6],
 [3,4,5],
 [0,3,0],
 [9,0,20]]
一种收集最多黄金的路线是：1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7。

提示：

-1 <= grid.length, grid[i].length <= 15
0 <= grid[i][j] <= 100
最多 25 个单元格中有黄金。

解法一

这题还是挺有意思的，填补了我一点二维平面回溯的空缺，其实也很简单（改了好几个小时还好意思说这种话😂）

private int[][] direction={{0,1},{1,0},{0,-1},{-1,0}};

public int getMaximumGold(int[][] grid) {
    int max=0;
    boolean[][] visit=new boolean[grid.length][grid[0].length];
    for (int i=0;i<grid.length;i++) {
        for (int j=0;j<grid[0].length;j++) {
            if (grid[i][j]>0) {
                max=Math.max(dfs(grid,i,j,visit),max);
            }
        }
    }
    return max;
}

//求出从 x,y 开始所能获得的最大的收益，记得回溯状态，后面的节点还需要遍历
public int dfs(int[][] grid,int x,int y,boolean[][] visit){
    int maxGlod=grid[x][y]; //一开始这里写的 0... 排了半天的错
    visit[x][y]=true;
    for (int i=0;i<direction.length;i++) {
        int nx=x+direction[i][0];
        int ny=y+direction[i][1];
        if (isValid(grid,nx,ny) && !visit[nx][ny] && grid[nx][ny]>0) {
            //求向 4 个方向扩展的最大值
            maxGlod=Math.max(dfs(grid,nx,ny,visit)+grid[x][y],maxGlod);
        }
    }
    visit[x][y]=false;
    return maxGlod;
}

public boolean isValid(final int[][] grid,int x,int y){
    return x>=0 && x<grid.length && y>=0 && y<grid[0].length;
}

思路其实也很简单，对每个有金矿的点进行 dfs 计算路径上的金矿和就 ok 了，但是这题有一个很关键的条件，不能回头，下过的金矿是不能第二次再进入的，不然这题就和前面的 [695. 岛屿最大面积](##695. 岛屿的最大面积)一样了，所以很显然这题是需要状态的回溯的，访问过的节点，后面的节点还是可能需要遍历的，最开始写的一个 bug 就是代码中提到的，那里一开始写的 0… 然后排错排了好长时间。菜啊

面试题 13. 机器人的运动范围

地上有一个 m 行 n 列的方格，从坐标 [0,0] 到坐标 [m-1,n-1] 。一个机器人从坐标 [0, 0] 的格子开始移动，它每次可以向左、右、上、下移动一格（不能移动到方格外），也不能进入行坐标和列坐标的数位之和大于 k 的格子。例如，当 k 为 18 时，机器人能够进入方格 [35, 37] ，因为 3+5+3+7=18。但它不能进入方格 [35, 38]，因为 3+5+3+8=19。请问该机器人能够到达多少个格子？

示例 1：

输入：m = 2, n = 3, k = 1
输出：3

示例 1：

输入：m = 3, n = 1, k = 0
输出：1

提示：

1 <= n,m <= 100
0 <= k <= 20

解法一

一开始没认真看例子，以为是求不能回头一次能走的最多的格子，原基础上稍微改一下就可以了

private int[][] direction={{1,0},{0,1},{0,-1},{-1,0}};

public int movingCount(int m, int n, int k) {
    return dfs(m,n,0,0,k,new boolean[m][n]);   
}

public int dfs(int m,int n,int x,int y,int k,boolean[][] visit){
    visit[x][y]=true;
    int res=1;
    for (int i=0;i<direction.length;i++) {
        int nx=x+direction[i][0];
        int ny=y+direction[i][1];
        if(valid(m,n,nx,ny,k) && !visit[nx][ny]){
            //以为是求最长的距离。....
            //res=Math.max(dfs(m,n,nx,ny,k,visit)+1,res);
            res+=dfs(m,n,nx,ny,k,visit);
        }
    }
    //visit[x][y]=false;
    return res;
}

public boolean valid(int m,int n,int x,int y,int k){
    if(x<0 || x>=m || y<0 || y>=n){
        return false;
    }
    int res=0;
    //35 37
    while(x!=0){
        res+=(x%10);
        x/=10;
    }
    while(y!=0){
        res+=(y%10);
        y/=10;
    }
    return res<=k;
}

1020. 飞地的数量

给出一个二维数组 A，每个单元格为 0（代表海）或 1（代表陆地）。

移动是指在陆地上从一个地方走到另一个地方（朝四个方向之一）或离开网格的边界。

返回网格中无法在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：

输入：[[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释： 
有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。

示例 2：

输入：[[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：
所有 1 都在边界上或可以到达边界。

提示：

1 <= A.length <= 500
1 <= A[i].length <= 500
0 <= A[i][j] <= 1
所有行的大小都相同

解法一

dfs 搜索就完事儿了，水题

//DFS
int[][] dir={{1,0},{0,1},{-1,0},{0,-1}};

public int numEnclaves(int[][] A) {
    if(A==null || A.length<=0) return 0;
    int N=A.length;
    int M=A[0].length;
    boolean[][] visit=new boolean[N][M];
    int a=0,b=0;
    while(a<N){ //左右边界
        if(A[a][0]==1 && !visit[a][0]) dfs(A,a,0,visit);
        if(A[a][M-1]==1 && !visit[a][M-1]) dfs(A,a,M-1,visit);
        a++;
    }
    while(b<M){ //上下边界
        if(A[0][b]==1&& !visit[0][b]) dfs(A,0,b,visit);
        if(A[N-1][b]==1&& !visit[N-1][b]) dfs(A,N-1,b,visit);
        b++;
    }
    int res=0;
    for (int i=0;i<N;i++) {
        for (int j=0;j<M;j++) {
            if(A[i][j]==1 && !visit[i][j]){
                res++;
            }
        }
    }
    return res;
}

public void dfs(int[][] A,int x,int y,boolean[][] visit){
    visit[x][y]=true;
    for (int i=0;i<dir.length;i++) {
        int nx=x+dir[i][0];
        int ny=y+dir[i][1];
        if(valid(A,nx,ny) && !visit[nx][ny] && A[nx][ny]==1){
            dfs(A,nx,ny,visit);
        }
    }
}

public boolean valid(final int[][] A,int x,int y){
    return x>=0 && x<A.length && y>=0 && y<A[0].length;
}

并查集的解法放在并查集专题中

934. 最短的桥

在给定的二维二进制数组 A 中，存在两座岛。（岛是由四面相连的 1 形成的一个最大组。）

现在，我们可以将 0 变为 1，以使两座岛连接起来，变成一座岛。

返回必须翻转的 0 的最小数目。（可以保证答案至少是 1。）

示例 1：

输入：[[0,1],[1,0]]
输出：1

示例 2：

输入：[[0,1,0],[0,0,0],[0,0,1]]
输出：2

示例 3：

输入：[[1,1,1,1,1],[1,0,0,0,1],[1,0,1,0,1],[1,0,0,0,1],[1,1,1,1,1]]
输出：1

提示：

1 <= A.length = A[0].length <= 100
A[i][j] == 0 或 A[i][j] == 1

解法一

这题还挺有意思的，dfs+bfs 都要用，单纯的深搜和广搜很难搞，先 dfs 给一个岛做标记，然后多源 bfs 找距离最近的另一个岛

int[] dir = {0, 1, 0, -1, 0};

public int shortestBridge(int[][] A) {
    boolean[][] mark = new boolean[A.length][A[0].length];
    lable:
    for (int i = 0; i < A.length; i++) {
        for (int j = 0; j < A[0].length; j++) {
            if (A[i][j] == 1) {
                dfs(A, i, j, mark);
                break lable;
            }
        }
    }
    Queue<Pair> queue = new LinkedList<>();
    for (int i = 0; i < A.length; i++) {
        for (int j = 0; j < A[0].length; j++) {
            if (A[i][j] == 1 && mark[i][j]) {
                queue.add(new Pair(i, j, 0));
            }
        }
    }
    while (!queue.isEmpty()) {
        Pair pair = queue.poll();
        for (int i = 0; i < 4; i++) {
            int nx = pair.x + dir[i];
            int ny = pair.y + dir[i + 1];
            if (valid(A, nx, ny) && !mark[nx][ny]) {
                if (A[nx][ny] == 1) {
                    return pair.step;
                }
                mark[nx][ny] = true;
                queue.add(new Pair(nx, ny, pair.step + 1));
            }
        }
    }
    return 1;
}

public void dfs(int[][] A, int x, int y, boolean[][] mark) {
    mark[x][y] = true;
    for (int i = 0; i < 4; i++) {
        int nx = x + dir[i];
        int ny = y + dir[i + 1];
        if (valid(A, nx, ny) && A[nx][ny] == 1 && !mark[nx][ny]) {
            dfs(A, nx, ny, mark);
        }
    }
}

public boolean valid(int[][] A, int x, int y) {
    return x >= 0 && x < A.length && y >= 0 && y < A[0].length;
}

class Pair {
    int x, y;
    int step;
    public Pair(int x, int y, int step) {
        this.x = x;
        this.y = y;
        this.step = step;
    }
}

733. 图像渲染

Difficulty: 简单

有一幅以二维整数数组表示的图画，每一个整数表示该图画的像素值大小，数值在 0 到 65535 之间。

给你一个坐标 (sr, sc) 表示图像渲染开始的像素值（行，列）和一个新的颜色值 newColor，让你重新上色这幅图像。

为了完成上色工作，从初始坐标开始，记录初始坐标的上下左右四个方向上像素值与初始坐标相同的相连像素点，接着再记录这四个方向上符合条件的像素点与他们对应四个方向上像素值与初始坐标相同的相连像素点，……，重复该过程。将所有有记录的像素点的颜色值改为新的颜色值。

最后返回经过上色渲染后的图像。

示例 1:

输入：
image = [[1,1,1],[1,1,0],[1,0,1]]
sr = 1, sc = 1, newColor = 2
输出：[[2,2,2],[2,2,0],[2,0,1]]
解析：
在图像的正中间，（坐标 (sr,sc)=(1,1)),
在路径上所有符合条件的像素点的颜色都被更改成 2。
注意，右下角的像素没有更改为 2，
因为它不是在上下左右四个方向上与初始点相连的像素点。

注意：

image 和 image[0] 的长度在范围 [1, 50] 内。
给出的初始点将满足 0 <= sr < image.length 和 0 <= sc < image[0].length。
image[i][j] 和 newColor 表示的颜色值在范围 [0, 65535]内。

解法一

经典搜索，没啥好说的

func floodFill(image [][]int, sr int, sc int, newColor int) [][]int {
    var m = len(image)
    var n = len(image[0])
    var dir = []int{1, 0, -1, 0, 1}
    var visit = make([][]bool, m)
    for i := 0; i < m; i++ {
        visit[i] = make([]bool, n)
    }
    var src = image[sr][sc]
    var valid = func(x int, y int) bool {
        return x >= 0 && x < m && y >= 0 && y < n
    }
    var dfs func(x int, y int)
    dfs = func(x int, y int) {
        visit[x][y] = true
        image[x][y] = newColor
        for i := 0; i < 4; i++ {
            var nx = x + dir[i]
            var ny = y + dir[i+1]
            if valid(nx, ny) && !visit[nx][ny] && image[nx][ny] == src {
                dfs(nx, ny)
            } 
        }
    }
    dfs(sr, sc)
    return image
}

通过染色的情况判断是否遍历过节点，节省 visit 数组

func floodFill(image [][]int, sr int, sc int, newColor int) [][]int {
    var m = len(image)
    var n = len(image[0])
    var dir = []int{1, 0, -1, 0, 1}
    var src = image[sr][sc]
    var valid = func(x int, y int) bool {
        return x >= 0 && x < m && y >= 0 && y < n
    }
    var dfs func(x int, y int)
    dfs = func(x int, y int) {
        image[x][y] = newColor
        for i := 0; i < 4; i++ {
            var nx = x + dir[i]
            var ny = y + dir[i+1]
            if valid(nx, ny) && image[nx][ny]!=newColor && image[nx][ny] == src {
                dfs(nx, ny)
            } 
        }
    }
    dfs(sr, sc)
    return image
}

1559. 二维网格图中探测环

Difficulty: 困难

给你一个二维字符网格数组 grid ，大小为 m x n ，你需要检查 grid 中是否存在 相同值 形成的环。

一个环是一条开始和结束于同一个格子的长度 大于等于 4 的路径。对于一个给定的格子，你可以移动到它上、下、左、右四个方向相邻的格子之一，可以移动的前提是这两个格子有 **相同的值 **。

同时，你也不能回到上一次移动时所在的格子。比方说，环 (1, 1) -> (1, 2) -> (1, 1) 是不合法的，因为从 (1, 2) 移动到 (1, 1) 回到了上一次移动时的格子。

如果 grid 中有相同值形成的环，请你返回 true ，否则返回 false 。

示例 1：

输入：grid = [["a","a","a","a"],["a","b","b","a"],["a","b","b","a"],["a","a","a","a"]]
输出：true
解释：如下图所示，有 2 个用不同颜色标出来的环：

示例 2：

输入：grid = [["c","c","c","a"],["c","d","c","c"],["c","c","e","c"],["f","c","c","c"]]
输出：true
解释：如下图所示，只有高亮所示的一个合法环：

示例 3：

输入：grid = [["a","b","b"],["b","z","b"],["b","b","a"]]
输出：false

提示：

m == grid.length
n == grid[i].length
1 <= m <= 500
1 <= n <= 500
grid 只包含小写英文字母。

解法一

33 双周赛的 T4，总体不是很难，dfs 或者并查集都可以

func containsCycle(grid [][]byte) bool {
    var m, n = len(grid), len(grid[0])
    var dir = [4][2]int{{0,1},{1,0},{-1,0},{0,-1}}
    var visit = make([][]bool, m)
    for i := 0; i < m; i++ {
        visit[i] = make([]bool, n)
    }
    var valid = func(x, y int) bool { return x >= 0 && x < m && y >= 0 && y < n}
    var dfs func (int, int, int, int)
    var res = false
    dfs = func(preX int, preY int, x int, y int) {
        if visit[x][y] || res{
            res = true
            return
        }
        visit[x][y] = true
        for i := 0; i < len(dir); i++ {
            nx := x + dir[i][0]
            ny := y + dir[i][1]
            //不走回头路
            if nx == preX && ny == preY {
                continue
            }
            if valid(nx, ny) && grid[nx][ny] == grid[x][y] {
                dfs(x, y, nx, ny)
            }
        }
    }
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            if !visit[i][j] {
                dfs(i,j,i,j)
            }
        }
    }
    return res
}

解法二

并查集的解法，留着以后再来写

332. 重新安排行程

Difficulty: 中等

给定一个机票的字符串二维数组 [from, to]，子数组中的两个成员分别表示飞机出发和降落的机场地点，对该行程进行重新规划排序。所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。

提示：

如果存在多种有效的行程，请你按字符自然排序返回最小的行程组合。例如，行程 [“JFK”, “LGA”] 与 [“JFK”, “LGB”] 相比就更小，排序更靠前
所有的机场都用三个大写字母表示（机场代码）。
假定所有机票至少存在一种合理的行程。
所有的机票必须都用一次且只能用一次。

示例 1：

输入：[["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
输出：["JFK", "MUC", "LHR", "SFO", "SJC"]

示例 2：

输入：[["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
输出：["JFK","ATL","JFK","SFO","ATL","SFO"]
解释：另一种有效的行程是 ["JFK","SFO","ATL","JFK","ATL","SFO"]。但是它自然排序更大更靠后。

解法一

欧拉回路，一笔画，后序遍历，先尝试完所有的子节点最后在添加当前节点，确保死胡同会被首先加入，这样 res 中就保持了答案的逆序

//欧拉回路，一笔画问题
func findItinerary(tickets [][]string) []string {
    var adj = make(map[string][]string)
    for _, tick := range tickets {
        adj[tick[0]] = append(adj[tick[0]], tick[1])
    }
    for _, toList := range adj {
        sort.Strings(toList)
    }
    var res []string
    var dfs func (cur string) 
    dfs = func (cur string) {
        for len(adj[cur]) != 0 {
            //删除节点，避免重复访问
            to := adj[cur][0]
            adj[cur] = adj[cur][1:]
            dfs(to)
        }
        //后序遍历，最后将路径添加进去，保证死胡同会首先加入
        res = append(res, cur)
    }
    dfs("JFK")
    //翻转下
    for i, j := 0, len(res)-1; i < j; i, j = i+1, j-1 {
        res[i], res[j] = res[j], res[i]
    }
    return res
}

841. 钥匙和房间

Difficulty: 中等

有 N 个房间，开始时你位于 0 号房间。每个房间有不同的号码：0，1，2，...，N-1，并且房间里可能有一些钥匙能使你进入下一个房间。

在形式上，对于每个房间 i 都有一个钥匙列表 rooms[i]，每个钥匙 rooms[i][j] 由 [0,1，...，N-1] 中的一个整数表示，其中 N = rooms.length。钥匙 rooms[i][j] = v 可以打开编号为 v 的房间。

最初，除 0 号房间外的其余所有房间都被锁住。

你可以自由地在房间之间来回走动。

如果能进入每个房间返回 true，否则返回 false。

示例 1：

输入：[[1],[2],[3],[]]
输出：true
解释：
我们从 0 号房间开始，拿到钥匙 1。
之后我们去 1 号房间，拿到钥匙 2。
然后我们去 2 号房间，拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间，我们返回 true。

示例 2：

输入：[[1,3],[3,0,1],[2],[0]]
输出：false
解释：我们不能进入 2 号房间。

提示：

1 <= rooms.length <= 1000
0 <= rooms[i].length <= 1000
所有房间中的钥匙数量总计不超过 3000。

解法一

没啥好说的

func canVisitAllRooms(rooms [][]int) bool {
    var n = len(rooms)
    var visit = make([]bool, n)
    var dfs func(int)
    var count = 0
    dfs = func(idx int) {
        visit[idx] = true
        count++
        for i := 0; i < len(rooms[idx]); i++ {
            if !visit[rooms[idx][i]] {
                dfs(rooms[idx][i])   
            }
        }
    }
    dfs(0)
    return count == n
}

分治

开个新坑，其实分治这个 tag 挺大的，很多题的做法都属于分治，而且涉及到分治的题目一般都还是有点难度的，不容易直接想出来

241. 为运算表达式设计优先级

给定一个含有数字和运算符的字符串，为表达式添加括号，改变其运算优先级以求出不同的结果。你需要给出所有可能的组合的结果。有效的运算符号包含 +, - 以及 * 。

示例 1:

输入："2-1-1"
输出：[0, 2]
解释：
((2-1)-1) = 0 
(2-(1-1)) = 2

示例 2:

输入："2*3-4*5"
输出：[-34, -14, -10, -10, 10]
解释：
(2*(3-(4*5))) = -34 
((2*3)-(4*5)) = -14 
((2*(3-4))*5) = -10 
(2*((3-4)*5)) = -10 
(((2*3)-4)*5) = 10

解法一

这题咋说呢，应该不算是回溯，是在分治 tag 中找的一题，还是挺有意思的

private Map<String,List<Integer>> map=new HashMap<>();

//分治
public List<Integer> diffWaysToCompute(String input) {
    if (input==null || input.length()<=0) {
        return new LinkedList<>();
    }
    return diffWaysToCompute(input,0,input.length()-1);
}

public List<Integer> diffWaysToCompute(String input,int left,int right) {
    List<Integer> res=new LinkedList<>();
    /*if (left==right) { //这一步可以去掉，最开始没考虑多位数的情况（考虑到了不知道怎么处理）
            res.add(Integer.valueOf(input.charAt(left))-48);
            return res;
        }*/
    String key=input.substring(left,right+1);
    if (map.containsKey(key)) {
        return map.get(key);
    }
    for (int i=left;i<=right;i++) { //大意了，这里一开始写成了 input.length...
        char c=input.charAt(i);
        if (c<'0') {
            List<Integer> leftCompute=diffWaysToCompute(input,left,i-1);
            List<Integer> rightCompute=diffWaysToCompute(input,i+1,right);
            for (int lc:leftCompute) {
                for (int rc:rightCompute) {
                    if (c=='+') 
                        res.add(lc+rc);
                    if (c=='-') 
                        res.add(lc-rc);
                    if (c=='*') 
                        res.add(lc*rc);
                }
            }
        }
    }
    if (res.isEmpty()) {
        res.add(Integer.valueOf(key));
    }
    map.put(key,res);
    return res;
}

第一天看了这道题，没想到思路，然后瞄了一眼评论区，看到了关键点，找到运算符，然后左右分别递归，没看到细节，第二天回忆了下思路写出了解，其实这题可以参考 95. 不同的二叉搜索树 II 我在我的二叉树专题中也加了这道题，两者解法极为相似

395. 至少有 K 个重复字符的最长子串

Difficulty: 中等

找到给定字符串（由小写字符组成）中的最长子串T，要求 T 中的每一字符出现次数都不少于 k 。输出 T的长度。

示例 1:

输入：
s = "aaabb", k = 3

输出：
3

最长子串为 "aaa" ，其中 'a' 重复了 3 次。

示例 2:

输入：
s = "ababbc", k = 2

输出：
5

最长子串为 "ababb" ，其中 'a' 重复了 2 次， 'b' 重复了 3 次。

解法一

以出现次数最少的字符为中点分治，但是效率感人，380ms+

public int longestSubstring(String s, int k) {
    if (s == null || s.length() == 0){
        return 0;
    }
    int[] count = new int[26];
    for(int i = 0; i < s.length(); i++){
        count[s.charAt(i)-'a']++;
    }
    int min = 0; //记录 count 最小的 index
    for(int i = 0;i < s.length(); i++){
        min = count[s.charAt(i)-'a'] < count[s.charAt(min)-'a'] ? i : min;
    }
    if (count[s.charAt(min)-'a'] >= k) {
        return s.length();
    }
    return Math.max(longestSubstring(s.substring(0,min),k),longestSubstring(s.substring(min+1),k));
}

解法二

参考了题解区大佬们的剪枝和优化方法，循环以每个小于 k 的字符为结尾，分割字符，多路分治，大大降低分治递归树的高度

//1ms 多路分治，虽然过了，但是感觉还是有点不流畅
//主要就是最后那个当以大于 k 的字符结尾的时候的额外处理，如果不 wa 一发不容易发现
public int longestSubstring(String s, int k) {
    if (s == null || s.length() == 0){
        return 0;
    }
    int[] count = new int[26];
    for(int i = 0; i < s.length(); i++){
        count[s.charAt(i)-'a']++;
    }
    int res = 0;
    int left = 0; //分治左端点
    boolean flag = false;
    for(int i = 0; i < s.length(); i++){
        if(count[s.charAt(i)-'a'] < k){
            flag = true;
            if(i - left >= res){ //剪枝优化
                res = Math.max(longestSubstring(s.substring(left,i),k),res);
            }
            left = i+1;
        }
    }
    if(!flag) return s.length();
    //上面分治的逻辑是以 left 到小于 k 的字母 i 进行分治，但是如果字符不是以小于 k 的字母结尾就无法计算
    //eg: aabbb k=3
    return Math.max(res,longestSubstring(s.substring(left),k));
}

其实还要很多分治的方法，但是感觉都大同小异

目录

LeetCode回溯&递归

Bug 警告

89. 格雷编码

Bug 警告！！！

二维平面上的回溯

分治