Tadowの自留地
文章 标签 分类 关于 SelfHost
Tadowの自留地

目录

LeetCode 单调栈

reso1mi 收录于 算法
   约 10351 字   预计阅读 21 分钟 

从 栈&队列专题 中抽取出来

496. 下一个更大元素 I

给定两个没有重复元素的数组 nums1 和 nums2 ，其中 nums1 是 nums2 的子集。找到 nums1 中每个元素在 nums2 中的下一个比其大的值。

nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在，对应位置输出-1。

示例 1:

输入：nums1 = [4,1,2], nums2 = [1,3,4,2].
输出：[-1,3,-1]
解释：
    对于 num1 中的数字 4，你无法在第二个数组中找到下一个更大的数字，因此输出 -1。
    对于 num1 中的数字 1，第二个数组中数字 1 右边的下一个较大数字是 3。
    对于 num1 中的数字 2，第二个数组中没有下一个更大的数字，因此输出 -1。

示例 2:

输入：nums1 = [2,4], nums2 = [1,2,3,4].
输出：[3,-1]
解释：
    对于 num1 中的数字 2，第二个数组中的下一个较大数字是 3。
    对于 num1 中的数字 4，第二个数组中没有下一个更大的数字，因此输出 -1。

注意：

  1. nums1和nums2中所有元素是唯一的。
  2. nums1和nums2 的数组大小都不超过 1000。

解法一

单调栈，很就之前在链表专题中做过一次 链表的下一个更大节点 但是没想起来，可能当时也没留下影响

这题其实还比原始的题加了一点难度，原始的题就是 num1==nums2 的情况，那样就不需要 HashMap 记录了

public int[] nextGreaterElement(int[] nums1, int[] nums2) {
    HashMap<Integer,Integer> map=new HashMap<>();
    Stack<Integer> stack=new Stack<>();
    for (int i=0;i<nums2.length;i++) {
        while(!stack.isEmpty() && nums2[stack.peek()]<nums2[i]){
            map.put(nums2[stack.pop()],nums2[i]);
        }
        stack.add(i);
    }
    int[] res=new int[nums1.length];
    for (int i=0;i<nums1.length;i++) {
        res[i]=map.getOrDefault(nums1[i],-1);
    }
    return res;
}

503. 下一个更大元素 II

给定一个循环数组（最后一个元素的下一个元素是数组的第一个元素），输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1。

示例 1:

输入：[1,2,1]
输出：[2,-1,2]
解释：第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

注意： 输入数组的长度不会超过 10000。

解法一

public static int[] nextGreaterElements(int[] nums) {
    if (nums==null || nums.length<=0) {
        return new int[]{};
    }
    Stack<Integer> stack=new Stack<>();
    stack.push(0);
    int[] res=new int[nums.length];
    Arrays.fill(res,-1);
    int index=1;
    for (int i=1;i<nums.length*2;i++) {
        index=i>=nums.length?i%nums.length:i;
        while(!stack.isEmpty()&&nums[stack.peek()]<nums[index]) {
            res[stack.pop()]=nums[index];
        }
        stack.push(index);
    }
    return res;
}

和上面一样，只不过需要循环遍历一遍，我最开始的做法相当憨憨，copy 了一个两倍的数组。还需要注意的就是 -1的处理

739. 每日温度

根据每日 气温 列表，请重新生成一个列表，对应位置的输入是你需要再等待多久温度才会升高超过该日的天数。如果之后都不会升高，请在该位置用 0 来代替。

例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。

提示：气温 列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度，都是在 [30, 100] 范围内的整数。

解法一

public int[] dailyTemperatures(int[] T) {
    int[] res=new int[T.length];
    if(T==null || T.length<=0) return res;
    Stack<Integer> stack=new Stack<>();
    stack.push(0);
    for (int i=1;i<T.length;i++) {
        while(!stack.isEmpty()&&T[stack.peek()]<T[i]){
            int temp=stack.pop();
            res[temp]=i-temp;
        }
        stack.push(i);
    }
    return res;
}

和上面两题一样，单调栈的解法，不过这题好像可以不用单调栈，可以从后向前递推

901. 股票价格跨度

编写一个 StockSpanner 类，它收集某些股票的每日报价，并返回该股票当日价格的跨度。

今天股票价格的跨度被定义为股票价格小于或等于今天价格的最大连续日数（从今天开始往回数，包括今天）。

例如，如果未来 7 天股票的价格是 [100, 80, 60, 70, 60, 75, 85]，那么股票跨度将是 [1, 1, 1, 2, 1, 4, 6]。

示例：

输入：["StockSpanner","next","next","next","next","next","next","next"], [[],[100],[80],[60],[70],[60],[75],[85]]
输出：[null,1,1,1,2,1,4,6]
解释：
首先，初始化 S = StockSpanner()，然后：
S.next(100) 被调用并返回 1，
S.next(80) 被调用并返回 1，
S.next(60) 被调用并返回 1，
S.next(70) 被调用并返回 2，
S.next(60) 被调用并返回 1，
S.next(75) 被调用并返回 4，
S.next(85) 被调用并返回 6。

注意 （例如） S.next(75) 返回 4，因为截至今天的最后 4 个价格
（包括今天的价格 75) 小于或等于今天的价格。

提示：

  • 调用 StockSpanner.next(int price) 时，将有 1 <= price <= 10^5
  • 每个测试用例最多可以调用 10000 次 StockSpanner.next
  • 在所有测试用例中，最多调用 150000 次 StockSpanner.next
  • 此问题的总时间限制减少了 50%

解法一

我起了，一枪秒了，有什么好说的

class StockSpanner {

    Deque<int[]> stack=new ArrayDeque<>();

    public StockSpanner() {}
    
    public int next(int price) {
        int res=1;
        while(!stack.isEmpty() && price>=stack.peek()[0]){
            res+=stack.pop()[1];
        }
        stack.push(new int[]{price,res});
        return res;
    }
}

84. 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

https://i.loli.net/2019/12/12/a7pVfNcYuIKFgwA.png

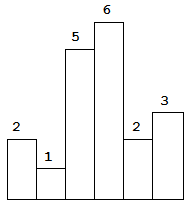
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

https://i.loli.net/2019/12/12/FAvMk3zWf4RheDi.png

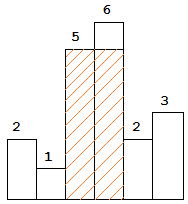
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例：

输入：[2,1,5,6,2,3]
输出：10

解法一

和上面几道题一样，单调栈的解法，这里是单调递增栈，20ms，87%

public int largestRectangleArea(int[] heights) {
    if (heights==null || heights.length<=0) {
        return 0;
    }
    Stack<Integer> stack=new Stack<>();
    int maxArea= Integer.MIN_VALUE;
    for (int i=0;i<heights.length;i++) {
        while(!stack.isEmpty() && heights[i]<=heights[stack.peek()]){
            //当前的柱子小于栈顶，说明当前栈顶最多向右扩展到 i-1
            int cur=stack.pop();
            //为空说明向左无法扩展，标为-1 不影响结果（可以提前将-1 压栈）
            int left=stack.isEmpty()?-1:stack.peek();
            //这里其实是 (i-1)-(left+1)+1
            maxArea=Math.max(maxArea,(i-left-1)*heights[cur]);
        }
        stack.push(i);
    }
    //处理栈中剩下的元素，右边是边界，剩余栈中所有的元素实际上都可以扩展到 heights.length-1
    //所以为了让所有的元素都能出栈，我们可以再数组的后面想象添加一个 0（也可以直接在原数组中添加一个 0)
    while(!stack.isEmpty()){ 
        int cur=stack.pop();
        int left=stack.isEmpty()?-1:stack.peek();
        //这一步很秀，在数组后面再想象一个 0 出来
        //让栈中元素向右扩张 (heights.length-1)-(left+1)+1
        maxArea=Math.max(maxArea,(heights.length-left-1)*heights[cur]);
    }
    return maxArea;
}

其实就是利用单调栈遍历每一个柱子，找到每一个柱子左边和右边第一个比它小的元素，比如左边第一个比当前柱子小的是 i，那么很显然 i+1 肯定是大于等于当前柱子的，并且 i+1 是左边连续大于当前柱子的最后一个，也就是当前柱子能想左扩展的边界位置，右边同理，既然是要求左右比当前柱子小的第一个，那么很明显就要用单调递增栈，然后就可以直接根据这两个数据计算完全包含当前柱子的最大的矩形的面积。

例如：3 4 5 4 3 6

首先3 4 5都顺利的存入栈中，此时栈中元素为【0，1，2】 ，当想存入下一个元素i=3,h[i]=4的时候，发现 4 比当前栈顶小，所以我们就可以开始计算完全包含栈中每个柱子的最大矩形的面积

  1. 由于当前i 位置的元素是比栈顶小，那么就说明 i-1 位置的元素一定比当前栈顶元素大！也就是向右边最多扩展到i-1位置

  2. 由于单调栈的结构，当前栈顶的下一个栈中元素left，其实就是当前栈顶的左边最近的比它小的元素，所以left+1位置的元素一定是比当前栈顶元素大（也有可能相等）！，所以向左边最多扩展到 left+1 位置

  3. 上面其实还分析漏了一种情况，那就是栈顶和i 位置元素相等的情况，第一点中提到的其实是 i 位置元素小于栈顶的情况，如果相等，那么向右能扩展到的位置还会是i-1么？显然不是，至少应该是i甚至更大，那我们这里计算的右边界不就是错误的？那我们将 = 去掉可以么？去掉之后单调栈就不再是严格单调了，这样的到的右边界确实准确了，但是我们的左边界由于栈中存在相等的元素，就变的不再准确了！

  4. 那我们如何处理这种情况呢？其实根本就不用处理，既然栈顶能向右扩展到 i-1 那么反过来，i-1 一样可以向左扩展到栈顶 位置，进而还可以扩展到left+1位置，而向左扩展的left+1是准确的，不会有误差，所以我们只需要等待i-1位置的元素弹出，然后就可以重新计算得到最大值，这个最大值肯定是包含之前的哪个最大当然这里其实那个 heights[i]<=heights[stack.peek()] 中的等号也可以去掉，这样栈就不是严格单调的了，left+1也不再准确，但是此时 i-1 就准确了，所以我们可以等待left+1 弹栈之后再重新计算，总而言之，就是相等的情况是不用做额外的处理

    http://static.imlgw.top/blog/20200129/gJPOkfEPDxwg.png?imageslim

    可以看到按照代码中的逻辑在计算完全包含当前绿色的栈顶元素的最大矩形的时候其实只计算到一部分，当计算到后面的相等的柱子的时候会完全包含之前的柱子的值，这样就不会有问题

​

经过上面的分析，代码就好写多了，不过这里还有一个地方值得注意，就是处理栈中剩余的元素，其实比较好的方法是在数组的末尾加一个 0，这样确保栈中所有的元素都可以出栈，不用额外的处理，java 中没法直接向数组中 push 元素，所以我们就想象末尾有一个 0，那么所有元素向左能扩展到的最远位置就是 heights.length-1

解法二

分治，480ms，27%

//分治 480ms
public int largestRectangleArea(int[] heights) {
    if (heights==null || heights.length<=0) {
        return 0;
    }
    largestRectangleArea(heights,0,heights.length-1);
    return maxArea;
}

private int maxArea=Integer.MIN_VALUE;

public void largestRectangleArea(int[] heights,int left,int right) {
    if (left>right) {
        return;
    }
    int minIndex=left;
    for (int i=left;i<=right;i++) {
        minIndex=heights[i]<heights[minIndex]?i:minIndex;
    }
    maxArea=Math.max(heights[minIndex]*(right-left+1),maxArea);
    largestRectangleArea(heights,left,minIndex-1);
    largestRectangleArea(heights,minIndex+1,right);
}

将数组区间以minIndex为分界线，分别求左边和右边的最大面积，时间复杂度O(NlogN)

解法三

优化的分治 1ms，100%，没想到比单调栈还快。

public int largestRectangleArea(int[] heights) {
    if (heights==null || heights.length<=0) {
        return 0;
    }
    return largestRectangleArea(heights,0,heights.length-1);
}

public int largestRectangleArea(int[] heights,int left,int right) {
    if (left>right) {
        return 0;
    }
    int minIndex=left;
    boolean up=true;
    boolean down=true;
    for (int i=left+1;i<=right;i++) {
        if (heights[i]<heights[i-1]) {
            up=false;
        }
        if (heights[i]>heights[i-1]) {
            down=false;
        }
        minIndex=heights[i]<heights[minIndex]?i:minIndex;
    }
    if (up) {
        int maxArea=-1;
        for (int i=left;i<=right;i++) {
            maxArea=Math.max(maxArea,(right-i+1)*heights[i]);
        }
        return maxArea;
    }
    if (down) {
        int maxArea=-1;
        for (int i=right;i>=left;i--) {
            maxArea=Math.max(maxArea,(i-left+1)*heights[i]);
        }
        return maxArea;
    }
    return Math.max(heights[minIndex]*(right-left+1),Math.max(largestRectangleArea(heights,minIndex+1,right),largestRectangleArea(heights,left,minIndex-1)));
}

其实相比于上面的分治，就是多了一步判断当前区间是否有序，因为有序的话就可以直接遍历得到区间的最大矩形，不用再递归做分治，我这里做了两个有序的判断，不知道是不是有的多余，我看的评论都只有一个

85. 最大矩形

给定一个仅包含 0 和 1 的二维二进制矩阵，找出只包含 1 的最大矩形，并返回其面积。

示例：

输入：
[
  ["1","0","1","0","0"],
  ["1","0","1","1","1"],
  ["1","1","1","1","1"],
  ["1","0","0","1","0"]
]
输出：6

解法一

特意在做了上面一题后没有马上做这一题，下面的是第二天下午做的，还行，没忘记😂，就是写的有点难看

//update: 2020.4.12
public int maximalRectangle(char[][] matrix) {
    if(matrix==null || matrix.length<=0) return 0;
    int M=matrix.length,N=matrix[0].length;
    int[][] height=new int[M][N+1]; //每一层多加一个 0, 方便后面出栈
    int res=0;
    for(int i=0;i<M;i++){
        for(int j=0;j<N;j++){
            if(matrix[i][j]=='1'){
                height[i][j]=i-1>=0?height[i-1][j]+1:1;
            }
        }
        res=Math.max(maxRectangle(height[i]),res);
    }
    return res;
}

public int maxRectangle(int[] height){
    Deque<Integer> stack=new ArrayDeque<>();
    int max=0;
    for(int i=0;i<height.length;i++){
        while(!stack.isEmpty() && height[i]<height[stack.peek()]){
            int cur=stack.pop();
            //栈为空的时候说明左边的全部是比当前栈顶大的元素，可以直接扩展到 0, 所以这里应该是-1
            int left=stack.isEmpty()?-1:stack.peek();
            //left+1 ~ i-1 = i-1-left
            max=Math.max((i-1-left)*height[cur],max);
        }
        stack.push(i);
    }
    return max;
}

其实计算 height 有一点动态规划的意思，我上面相当于写了个二维的动态规划

2020.4.12 重写了一遍，然后更新了代码，之前的代码不够简洁

解法二

public int maximalRectangle(char[][] matrix) {
    if (matrix==null || matrix.length<=0) {
        return 0;
    }
    //初始化 height 数组，在末尾添加一个元素（默认 0) 让所有元素可以出栈
    int[] height=new int[matrix[0].length+1];
    int max=0;
    //记录每一层的 height
    for (int i=0;i<matrix.length;i++) {
        for (int j=0;j<matrix[0].length;j++) {
            height[j]=matrix[i][j]=='1'?height[j]+1:0;
        }
        max=Math.max(max,maxArea(height));
    }
    return max;
}

maxArea可以直接采用上面 84 题的分治

581. 最短无序连续子数组

给定一个整数数组，你需要寻找一个连续的子数组，如果对这个子数组进行升序排序，那么整个数组都会变为升序排序。

你找到的子数组应是最短的，请输出它的长度。

示例 1:

输入：[2, 6, 4, 8, 10, 9, 15]
输出：5
解释：你只需要对 [6, 4, 8, 10, 9] 进行升序排序，那么整个表都会变为升序排序。

说明 :

  1. 输入的数组长度范围在 [1, 10,000]。
  2. 输入的数组可能包含重复元素 ，所以升序的意思是**<=。**

解法一

单调栈的解法明天再写

鸽了挺长时间，单调栈的解法还是挺好的

public int findUnsortedSubarray(int[] nums) {
    Stack<Integer> stack=new Stack<>();
    int left=Integer.MAX_VALUE,right=Integer.MIN_VALUE;
    for (int i=0;i<nums.length;i++) {
        while(!stack.isEmpty() && nums[stack.peek()]>nums[i]){
            left=Math.min(stack.pop(),left); //左边界正确位置（最小值）
        }
        stack.push(i);
    }
    stack.clear();
    for (int i=nums.length-1;i>=0;i--) {
        while(!stack.isEmpty() && nums[stack.peek()]<nums[i]){
            right=Math.max(stack.pop(),right); //右边界正确位置（最大值）
        }
        stack.push(i);
    }
    return left>right?0:right-left+1;
}

第一个单调栈中存的是从左到右递增的序列，当遇到nums[i]小于栈顶时，说明这个位置是错位的，正确的位置应该是栈顶的元素的位置，我们这里求的就是一个最小的错位的索引

第二个单调栈中存的是从右向左递减的序列，当遇到nums[i]大于栈顶时，说明这个位置是错位的，正确的位置应该是栈顶的元素，这里求的就是一个最大的错位的索引 ，两者之间的距离其实就是我们最终要求的最短无序子数组长度

解法二

其实和上面的单调栈的思路是一样的，都是找第一个（最小）和最后一个（最大）错位的元素，但是这里我们求出错位的元素后还需要再遍历找到原本正确的位置，

//O(1) 空间的解法
public int findUnsortedSubarray(int[] nums) {
    if (nums[0]>nums[nums.length-1]) {
        return nums.length;
    }
    int max=Integer.MIN_VALUE,min=Integer.MAX_VALUE;
    for (int i=1;i<nums.length;i++) {
        if (nums[i]<nums[i-1]) {
            min=Math.min(min,nums[i]); //无序序列中的最小值
        }
    }

    for (int i=nums.length-1;i>0;i--) {
        if (nums[i]<nums[i-1]) {
            max=Math.max(max,nums[i-1]); //无序序列中的最大值
        }
    }
    int left=0,right=nums.length-1;
    while(left<nums.length){
        if (nums[left]>min) {
            break;
        }
        left++; //左边界正确位置
    }
    while(right>=0){
        if (nums[right]<max) {
            break;
        }
        right--; //右边界正确位置
    }
    return right<left?0:right-left+1;
}

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

https://i.loli.net/2019/05/14/5cda71129045d93180.png

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例：

输入：[0,1,0,2,1,0,1,3,2,1,2,1]
输出：6

解法三

单调栈解法，双指针的解法放在 数组专题 中，其实我感觉熟悉单调栈的话，单调栈的解法会比其他方法更好理解

public static int trap6(int[] height) {
    if (height == null || height.length == 0) return 0;
    Deque<Integer> stack = new ArrayDeque<>(); //栈里面维护一个递减序列
    int res = 0;
    for (int i = 0; i < height.length; i++){
        while ( ! stack.isEmpty() && height[stack.peek()] < height[i]) { //当遍历的元素大于栈顶元素
            int tmp = stack.pop(); //栈顶弹出来
            if (stack.isEmpty()) break;
            res += (Math.min(height[i],height[stack.peek()]) - height[tmp]) * (i - stack.peek() - 1);
        }
        //维护递减序列
        stack.push(i);
    }
    return res;
}

单调递减栈，栈中存柱子的索引，当遇到大于栈顶的元素的时候就开始弹栈，计算栈顶元素和左右首个大于栈顶元素的所能构成的那一层的接水量，对应下面的图理解就是

(Math.min(height[i],height[stack.peek()])-curTop) * (i-stack.peek()-1)

http://static.imlgw.top/blog/20200129/f0b4lo2Xk5Q3.png?imageslim

依次计算①②③位置的面积，这样的思路感觉会更加的自然

面试题 33. 二叉搜索树的后序遍历序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

     5
    / \
   2   6
  / \
 1   3

示例 1：

输入：[1,6,3,2,5]
输出：false

示例 2：

输入：[1,3,2,6,5]
输出：true

提示：

  1. 数组长度 <= 1000

解法一

单调栈的解法

public boolean verifyPostorder(int[] postorder) {
    if(postorder==null || postorder.length<=0) return true;
    Deque<Integer> stack=new ArrayDeque<>();
    //1 2 | 4 5 | 3
    int curRoot=Integer.MAX_VALUE;
    for(int i=postorder.length-1;i>=0;i--){
        if(postorder[i]>curRoot){
            return false;
        }
        while(!stack.isEmpty() && postorder[i]<postorder[stack.peek()]){
            curRoot=postorder[stack.pop()];
        }
        stack.push(i);
    }
    return true;
}

逆序遍历这个序列，就是 root -- root.right -- root.left ，用一个单调递增栈，当遇到减小的值就说明进入了左子树，我们需要找到这颗树的根节点，也就是不停出栈，直到找到根节点，然后继续向后判断左子树是不是都小于这个根节点的

面试题 59 - II. 队列的最大值

请定义一个队列并实现函数 max_value 得到队列里的最大值，要求函数 max_value、push_back 和 pop_front 的时间复杂度都是 O(1)。

若队列为空，pop_front 和 max_value 需要返回 -1

示例 1：

输入：
["MaxQueue","push_back","push_back","max_value","pop_front","max_value"]
[[],[1],[2],[],[],[]]
输出：[null,null,null,2,1,2]

示例 2：

输入：
["MaxQueue","pop_front","max_value"]
[[],[],[]]
输出：[null,-1,-1]

限制：

  • 1 <= push_back,pop_front,max_value 的总操作数 <= 10000
  • 1 <= value <= 10^5

解法一

public MaxQueue() {

}

Deque<Integer> queue=new LinkedList<>();

Deque<Integer> maxQueue=new ArrayDeque<>();

public int max_value() {
    return maxQueue.isEmpty()?-1:maxQueue.getFirst();
}

public void push_back(int value) {
    queue.addLast(value);
    while(!maxQueue.isEmpty() && value>maxQueue.getLast()){
        maxQueue.removeLast();
    }
    maxQueue.addLast(value);
}

public int pop_front() {
    if(queue.isEmpty()) return -1;
    int temp=queue.removeFirst();
    if(temp==maxQueue.getFirst()){
        maxQueue.removeFirst();
    }
    return temp;
}

一直以为是和最小栈一样，结果 WA 了两发才意识到搞错了。这里是一个队列，进出方向是不一样的

其实这题和之前的一道 滑动窗口最大值 一样，维护一个单调递减的单调栈然后维护这个单调栈就行了

5402. 绝对差不超过限制的最长连续子数组

给你一个整数数组 nums ，和一个表示限制的整数 limit，请你返回最长连续子数组的长度，该子数组中的任意两个元素之间的绝对差必须小于或者等于 limit 。

如果不存在满足条件的子数组，则返回 0 。

示例 1：

输入：nums = [8,2,4,7], limit = 4
输出：2 
解释：所有子数组如下：
[8] 最大绝对差 |8-8| = 0 <= 4.
[8,2] 最大绝对差 |8-2| = 6 > 4. 
[8,2,4] 最大绝对差 |8-2| = 6 > 4.
[8,2,4,7] 最大绝对差 |8-2| = 6 > 4.
[2] 最大绝对差 |2-2| = 0 <= 4.
[2,4] 最大绝对差 |2-4| = 2 <= 4.
[2,4,7] 最大绝对差 |2-7| = 5 > 4.
[4] 最大绝对差 |4-4| = 0 <= 4.
[4,7] 最大绝对差 |4-7| = 3 <= 4.
[7] 最大绝对差 |7-7| = 0 <= 4. 
因此，满足题意的最长子数组的长度为 2 。

示例 2：

输入：nums = [10,1,2,4,7,2], limit = 5
输出：4 
解释：满足题意的最长子数组是 [2,4,7,2]，其最大绝对差 |2-7| = 5 <= 5 。

示例 3：

输入：nums = [4,2,2,2,4,4,2,2], limit = 0
输出：3

提示：

  • 1 <= nums.length <= 10^5
  • 1 <= nums[i] <= 10^9
  • 0 <= limit <= 10^9

187th 周赛 t3，时隔这么久又回头打一次周赛，可惜，又只做了两题，前两题 10 分钟不到就写完了，心想这回怎么说也得做个 3 题，结果。

解法一

public int longestSubarray2(int[] nums, int limit) {
    if (nums==null || nums.length<=0) {
        return 0;
    }
    int left=0,right=0;
    int min=0,max=0;
    int res=1;
    PriorityQueue<Integer> minpq=new PriorityQueue<>();
    minpq.add(nums[0]);
    PriorityQueue<Integer> maxpq=new PriorityQueue<>((a,b)->b-a);
    maxpq.add(nums[0]);
    //7 2
    while(left<=right && right<nums.length){
        while (right< nums.length && maxpq.peek()-minpq.peek()<=limit) {
            res=Math.max(right-left+1,res);
            right++;
            if (right<nums.length) {
                maxpq.add(nums[right]);
                minpq.add(nums[right]);   
            }
        }
        maxpq.remove(nums[left]);
        minpq.remove(nums[left]);
        left++;
    }
    return res;
}

这个是当时比赛调了半天没调出来，结束之后调出来的代码，用两优先队列维护区间最值，然后滑窗就行了，我这里就是调滑窗的时候调了半天，之前写滑窗就是乱写的，没什么章法，边 WA 边改，看来最近得好好总结下滑窗的题了，得搞个板子出来

解法二

最优解，O(N) 单调队列

//UPDATE: 2020/6/29 改成最近总结的 for-while 滑窗模板
//上面的解法一的滑窗也写的不好，有时间改改
public int longestSubarray(int[] nums, int limit) {
    if (nums==null || nums.length<=0) {
        return 0;
    }
    int left=0;
    int min=0,max=0;
    int res=1;
    //单调队列记录区间最值索引
    LinkedList<Integer> maxQue=new LinkedList<>();
    LinkedList<Integer> minQue=new LinkedList<>();
    for(int right=0;right<nums.length;right++){
        while(!maxQue.isEmpty() && nums[maxQue.getLast()]<nums[right]){
            maxQue.removeLast();
        }
        maxQue.addLast(right);
        while(!minQue.isEmpty() && nums[minQue.getLast()]>nums[right]){
            minQue.removeLast();
        }
        minQue.addLast(right);
        while(nums[maxQue.getFirst()]-nums[minQue.getFirst()]>limit) {
            //不符合要求，左边界左移，当左边界是最值的时候 que 弹出
            if (left==maxQue.getFirst()) maxQue.removeFirst();
            if (left==minQue.getFirst()) minQue.removeFirst();
            left++;
        }
        res=Math.max(res,right-left+1);
    }
    return res;
}

其实当时我确实也尝试去用两个单调队列维护最值，但是！！！还是被滑窗的边界给搞得不知道这么写了，然后就没又然后了，上面的代码也是比赛完之后自己写出来的，说到底还是菜啊！😭

962. 最大宽度坡

给定一个整数数组 A，坡是元组 (i, j)，其中 i < j 且 A[i] <= A[j]。这样的坡的宽度为 j - i。

找出 A 中的坡的最大宽度，如果不存在，返回 0 。

示例 1：

输入：[6,0,8,2,1,5]
输出：4
解释：
最大宽度的坡为 (i, j) = (1, 5): A[1] = 0 且 A[5] = 5.

示例 2：

输入：[9,8,1,0,1,9,4,0,4,1]
输出：7
解释：
最大宽度的坡为 (i, j) = (2, 9): A[2] = 1 且 A[9] = 1.

提示：

  1. 2 <= A.length <= 50000
  2. 0 <= A[i] <= 50000

解法一

想不到，着实想不到，这个单调栈的用法确实没见过

public int maxWidthRamp(int[] A) {
    Deque<Integer> stack=new ArrayDeque<>();
    int res=0;
    for(int i=0;i<A.length;i++){
        if(stack.isEmpty() || A[stack.peek()]>A[i]){
            stack.push(i);
        }
    }
    for(int i=A.length-1;i>=0;i--){
        while(!stack.isEmpty() && A[stack.peek()]<=A[i]){
            int cur=stack.pop();
            res=Math.max(res,i-cur);
        }
    }
    return res;
}

首先把 A 数组中的以A[0]开头的递减序列抽取出来，我们最后要求的最大的宽度坡一定是以这个序列中的某一个i为坡底的，我们反证一下

假设存在某个元素位置k不存在于上面的递减序列中，且有最大宽度j-k，这也就说明k位置的元素一定是小于等于 k 前面所有的元素的，否则就会有更长的宽度，但是既然k小于等于前面所有的元素，那么 k 就一定会被加入到序列中，与假设矛盾，所以不存在 k，解一定存在递减序列中

这样的话我们可以逆向遍历数组，每次遇到元素大于栈顶的就可以计算宽度，然后将栈顶弹出，因为是逆序遍历的，所以这个宽度一定是栈顶这个**坡底 i **能形成的最大宽度了， 逆序遍历再往前的话即使大于这个栈顶，形成的宽度也只会减小，所以这个栈顶是可以直接pop出去的，我们遍历所有的坡底求最大值就行了，时间复杂度O(N)

解法二

二分的思路，和上面一样，先构建一个以A[0]开头的递减序列，这里面就是我们所有的坡底，然后我们可以遍历所有的元素，然后在这个单调序列中寻找第一个小于等于当前元素的index，这两个构成的宽度就是当前元素所能形成的最大宽度，我们求出所有的最大宽度取一个最值就可以了，时间复杂度O(NlogN)

func maxWidthRamp(A []int) int {
    var order [][]int
    order = append(order, []int{0, A[0]})
    //构建递减序列
    for i := 1; i < len(A); i++ {
        if A[i] < order[len(order)-1][1] {
            order = append(order, []int{i, A[i]})
        }
    }
    res := 0
    for j, target := range A {
        i := binarySearch(order, target)
        res = Max(res, j-i)
    }
    return res
}

//找第一个小于等于 target 的值
func binarySearch(num [][]int, target int) int {
    left := 0
    right := len(num) - 1
    for left < right {
        mid := left + (right-left)/2
        if num[mid][1] > target {
            left = mid + 1 //注意是递减序列
        } else {
            right = mid
        }
    }
    return num[left][0]
}

func Max(a, b int) int {
    if a > b {
        return a
    }
    return b
}

在 lc 写的 题解 欢迎前来纠错

1124. 表现良好的最长时间段

给你一份工作时间表 hours，上面记录着某一位员工每天的工作小时数。

我们认为当员工一天中的工作小时数大于 8 小时的时候，那么这一天就是「劳累的一天」。

所谓「表现良好的时间段」，意味在这段时间内，「劳累的天数」是严格 大于「不劳累的天数」。

请你返回「表现良好时间段」的最大长度。

示例 1：

输入：hours = [9,9,6,0,6,6,9]
输出：3
解释：最长的表现良好时间段是 [9,9,6]。

提示：

  • 1 <= hours.length <= 10000
  • 0 <= hours[i] <= 16

解法一

惭愧，这题还是看的题解，这题还是挺巧妙的，我们把大于 8 小时的时间段看作+1，小于 8 小时的看作-1，这样问题就转换成了求区间和大于 0 的最长长度，而区间和我们又可以联想到用前缀和，这样我们将题目的例子转换一下就变成了

hours:    9 9  6  0  6  6  9
hours:  0 1 1 -1 -1 -1 -1  1
  pre:  0 1 2  1  0 -1 -2 -1

只要pre中两点的前缀pre[j]-pre[i]>0就说明区间[i+1，j]是满足条件的，我们要求的就是满足条件的最长宽度，这样一来问题其实就转换成了和上面 962. 最大宽度坡一样了，我们按照上面的步骤求解就 ok 了

public int longestWPI(int[] hours) {
    int[] pre=new int[hours.length+1];
    for(int i=1;i<=hours.length;i++){
        pre[i]=pre[i-1]+(hours[i-1]>8?1:-1);
    }
    Deque<Integer> stack=new ArrayDeque<>();
    for(int i=0;i<pre.length;i++){
        if(stack.isEmpty() || pre[i]<pre[stack.peek()]){
            stack.push(i);
        }
    }
    int res=0;
    for(int i=pre.length-1;i>=0;i--){
        while(!stack.isEmpty() && pre[i]-pre[stack.peek()]>0){
            res=Math.max(res,i-stack.pop()); //不用+1
        }
    }
    return res;
}

907. 子数组的最小值之和

给定一个整数数组 A，找到 min(B) 的总和，其中 B 的范围为 A 的每个（连续）子数组。

由于答案可能很大，因此返回答案模 10^9 + 7。

示例：

输入：[3,1,2,4]
输出：17
解释：
子数组为 [3]，[1]，[2]，[4]，[3,1]，[1,2]，[2,4]，[3,1,2]，[1,2,4]，[3,1,2,4]。 
最小值为 3，1，2，4，1，1，2，1，1，1，和为 17。

提示：

  1. 1 <= A <= 30000
  2. 1 <= A[i] <= 30000

解法一

虽然花了挺长时间好歹还是自己做出来了，开心😁

public int sumSubarrayMins(int[] A) {
    Deque<Integer> stack=new ArrayDeque<>();
    int N=A.length;
    int mod=(int)1e9+7;
    int res=0;
    int[] temp=new int[N+1];
    System.arraycopy(A,0,temp,0,N);
    //末尾加 0 使所有元素都可以出栈
    temp[N]=0;A=temp; 
    for(int i=0;i<N+1;i++){
        while(!stack.isEmpty() && A[stack.peek()]>A[i]){
            int cur=stack.pop();
            int left=stack.isEmpty()?-1:stack.peek();
            //右边大于 cur 的个数 (i 之前）： i-cur-1      
            //左边大于 cur 的个数 (left 之后）： cur-(left+1) 
            //res=(res+A[cur]*((i-cur-1)*(cur-left-1)+i-1-left))%mod;
            //(a+1)*(b+1)=ab+a+b+1
            res=(res+A[cur]*(i-cur)*(cur-left))%mod;
        }
        stack.push(i);
    }
    return res;
}

核心思想就是维护单调递增栈，在每个元素出栈的时候考虑如何计算以该元素为区间最小值的区间个数

比如[9,8,7,6,1,5,3,4,2]这个区间，我们要求以1为区间最小值的区间个数。

我们分开来求，先求左右两边的，很明显仅包含1左边或右边元素的子区间个数是 4+4=8 个，也就是 [6,1] , [7,6,1] … 和 [1,5], [1,5,3]…. 这些区间

然后再看同时包含1左右两边的元素的子区间，一边选一个区间和另一边都会有 4 种组合，所以就是 4*4=16 种

最后再加上1本身就行了，所以以1为区间最小值的区间个数就是 8+16+1=25

在看了大佬的做法后发现上面的是可以化简的：a*b+a+b+1=(a+1)*(b+1)

5454. 统计全 1 子矩形

Difficulty: 中等

给你一个只包含 0 和 1 的 rows * columns 矩阵 mat ，请你返回有多少个 子矩形 的元素全部都是 1 。

示例 1：

输入：mat = [[1,0,1],
            [1,1,0],
            [1,1,0]]
输出：13
解释：
有 6 个 1x1 的矩形。
有 2 个 1x2 的矩形。
有 3 个 2x1 的矩形。
有 1 个 2x2 的矩形。
有 1 个 3x1 的矩形。
矩形数目总共 = 6 + 2 + 3 + 1 + 1 = 13 。

示例 2：

输入：mat = [[0,1,1,0],
            [0,1,1,1],
            [1,1,1,0]]
输出：24
解释：
有 8 个 1x1 的子矩形。
有 5 个 1x2 的子矩形。
有 2 个 1x3 的子矩形。
有 4 个 2x1 的子矩形。
有 2 个 2x2 的子矩形。
有 2 个 3x1 的子矩形。
有 1 个 3x2 的子矩形。
矩形数目总共 = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24 。

示例 3：

输入：mat = [[1,1,1,1,1,1]]
输出：21

示例 4：

输入：mat = [[1,0,1],[0,1,0],[1,0,1]]
输出：5

提示：

  • 1 <= rows <= 150
  • 1 <= columns <= 150
  • 0 <= mat[i][j] <= 1

解法一

196 周赛 T3，感觉还是挺难的，不过数据量比较小，只有 150，所以暴力其实就可以

//解法一：N3
public int numSubmat(int[][] mat) {
    int m = mat.length;
    int n = mat[0].length;
    //预处理 mat[i][j] 上边有多少个连续的 1
    int[][] upCnt= new int[m][n];
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if(mat[i][j] == 1){
                upCnt[i][j] = i==0 ? mat[i][j]&1 : upCnt[i-1][j]+1;
            }
        }
    }
    int res = 0;
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if(mat[i][j] == 1){
                int k = j;
                int rowCnt = upCnt[i][j];
                while(k>=0){
                    rowCnt = Math.min(rowCnt, upCnt[i][k]);
                    res += rowCnt;
                    k--;
                }
            }
        }
    }
    return res;
}

解法二

单调栈，参考了网上的题解，虽然自己搞懂了，但是想写题解的时候感觉有点不好描述啊，要写好多东西，有点抽象，但是思路还是非常好的，也是个很经典的题了

public int numSubmat(int[][] mat) {
    int m = mat.length;
    int n = mat[0].length;
    //预处理 mat[i][j] 上边有多少个连续的 1
    int[][] upCnt= new int[m][n];
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if(mat[i][j] == 1){
                upCnt[i][j] = i==0 ? mat[i][j]&1 : upCnt[i-1][j]+1;
            }
        }
    }
    //单调递增栈维护列的长度
    Deque<Integer> stack = new ArrayDeque<>();
    int res = 0;
    for (int i = 0; i < m; i++) {
        stack.clear();
        int ijCnt = 0; //以 i,j 为右下角的矩形的 cnt
        for (int j = 0; j < n; j++) {
            ijCnt += upCnt[i][j];
            while(!stack.isEmpty() && upCnt[i][stack.peek()] > upCnt[i][j]){
                int cur = stack.pop();
                //栈中的索引是从 0 开始的，所以这里如果栈为空，left 应该为-1
                int left = stack.isEmpty() ? -1 : stack.peek();
                //减去多的部分
                ijCnt -= (cur-left) * (upCnt[i][cur] - upCnt[i][j]);
            }
            stack.push(j);
            res += ijCnt;
        }
    }
    return res;
}

为了方便回顾，简单的画了个图 http://static.imlgw.top/blog/20200705/BDIQmVW7vEuT.png?imageslim

这题好像是个很经典的题，我在网上搜索的的时候发现和 ICPC 的一道题 一样

解法三

在刷了几遍评论区，看见了大佬们写的比较好解法，发现了一个比较容易理解的单调栈的思路

（1）第一步预处理和上面是一样的，统计每个元素向上延申的最大值 （2）然后我们同样使用单调递增栈维护这个高度，但是同时我们额外的维护另一个值：以当前mat[i][j]为右下角所形成的矩形个数也存入单调栈 ，然后我们在每个元素进栈的时候统计个数，统计一共分为两部分：

http://static.imlgw.top/blog/20200828/x8M127uqudmS.png?imageslim （2020.8.28 更新了一下，之前的图有点抽象）

public int numSubmat(int[][] mat) {
    int m = mat.length;
    int n = mat[0].length;
    //预处理 mat[i][j] 上边有多少个连续的 1
    int[][] upCnt= new int[m][n];
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            if(mat[i][j] == 1){
                upCnt[i][j] = i==0 ? mat[i][j]&1 : upCnt[i-1][j]+1;
            }
        }
    }
    //单调递增栈维护列的长度
    Deque<int[]> stack = new ArrayDeque<>();
    int res = 0;
    for(int i = 0;i < m; i++){
        stack.clear();
        for (int j = 0; j < n; j++) {
            while(!stack.isEmpty() && upCnt[i][stack.peek()[0]] > upCnt[i][j]){
                stack.pop();
            }
            int[] pair = stack.isEmpty() ? new int[]{-1,0} : stack.peek();
            //以当前栈顶元素 mat[i][pair[0]] 为右下角能形成矩形个数
            int cur = (j-pair[0]) * upCnt[i][j] + pair[1];
            res += cur;
            //将 mat[i][j] 的索引 j 和以其为右下角形成的矩阵个数 cur 也存入单调栈
            stack.push(new int[]{j, cur});
        }
    }
    return res;
}

这个思路比上面要容易理解多了

面试题 03.05. 栈排序

Difficulty: 中等

栈排序。 编写程序，对栈进行排序使最小元素位于栈顶。最多只能使用一个其他的临时栈存放数据，但不得将元素复制到别的数据结构（如数组）中。该栈支持如下操作：push、pop、peek 和 isEmpty。当栈为空时，peek 返回 -1。

示例 1:

 输入：
["SortedStack", "push", "push", "peek", "pop", "peek"]
[[], [1], [2], [], [], []]
 输出：
[null,null,null,1,null,2]

示例 2:

 输入： 
["SortedStack", "pop", "pop", "push", "pop", "isEmpty"]
[[], [], [], [1], [], []]
 输出：
[null,null,null,null,null,true]

说明：

  1. 栈中的元素数目在 [0, 5000] 范围内。

解法一

之前在书上看到过这一题，但是时间久了忘了咋做了，只记得是单调栈，思考了下还是写出来了

单调栈，主栈单调递减（自顶向下），当遇到大于栈顶的元素就弹栈，并将弹出的元素用辅助栈接收，完事了再将元素 push 进去，最后将辅助栈中的元素再倒回去就 ok 了，时间复杂度 N^2

class SortedStack {
    
    Deque<Integer> stack = null;
    
    Deque<Integer> help = null;
    //单调栈排序
    //4 3 2 1 3 4 2
    public SortedStack() {
        stack = new ArrayDeque<>();
        help = new ArrayDeque<>();
    }
    
    public void push(int val) {
        //一开始写成 pop 了找半天的错
        while(!stack.isEmpty() && stack.peek() < val) {
            help.push(stack.pop());
        }
        stack.push(val);
        //再装回去
        while(!help.isEmpty()) {
            stack.push(help.pop());
        }
    }
    
    public void pop() {
        if (!stack.isEmpty()) {
            stack.pop();
        }
    }
    
    public int peek() {
        if (stack.isEmpty()) {
            return -1;
        }
        return stack.peek();
    }
    
    public boolean isEmpty() {
        return stack.isEmpty();
    }
}

NC580. 抢打出头鸟

现在有 n 个人站成一列，第 i 个人的身高为a[i]他们人手一把玩具枪，并且他们喜欢把枪举在头顶上。 每一次练习射击，他们都会朝正前方发射一发水弹。 这个时候，第 i 个人射击的水弹，就会击中在他前面第一个比他高的人。 牛牛认为这样的练习十分的荒唐，完全就是对长得高的人的伤害。 于是它定义了一个荒唐度，初始为 0。 对于第 i 个人，如中他击中了第 j 个人，则荒唐度加 j，如果没有击中任何人，则荒唐度加 0. 牛牛想问你，你能计算出荒唐度是多少吗？

输入

一个整数 n（1 ≤ n ≤ 10^7），一个数组 a (1 ≤ a[i] ≤ 10^7) a 下标从 0 开始，a[i] 代表第 i 个人身高

示例 1

输入：5,[1,2,3,4,5]
输出：0
说明：没有一个人击中任何一个人

示例 2

输入：5,[5,4,3,2,1]
输出：10
说明：第二个人击中第一个人，第三个人击中第二个人，第四个人击中第三个人，第五个人击中第四个人； 1+2+3+4=10

解法一

很直白的单调栈，但是一开始被题目的 case 误导了下，搞了一个单调递增栈，这里很很明显应该是递减栈，递增栈会把原本大的值给 pop 出去

//5 4 3 4 1
//一开始被例子给误导了，搞了一手单调递增栈。...
public long solve (int n, int[] a) {
    Deque<Integer> stack = new ArrayDeque<>();
    long res = 0l;
    for (int i = 0; i < n; i++) {
        while (!stack.isEmpty() && a[stack.peek()] <= a[i]) {
            stack.pop();
        }
        if (!stack.isEmpty()) {
            res += stack.peek()+1;
        }
        stack.push(i);
    }
    return res;
}
更新于 2020-08-28
 LeetCode
返回 | 主页