LeetCode动态规划
70. 爬楼梯
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Note: Given n will be a positive integer.
Example 1:
Input: 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
Example 2:
Input: 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
解法一
没啥好说的,可以说是最经典的 dp 题了
public static int climbStairsDp(int n){
int []dp=new int[n+1];
dp[0]=1;
dp[1]=1;
for (int i=2;i<=n;i++) {
dp[i]=dp[i-1]+dp[i-2];
}
return dp[n];
}
198. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
Example 1:
Input: [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.
Example 2:
Input: [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
Total amount you can rob = 2 + 9 + 1 = 12.
解法一
简单的 dp 题,dp 方程很容易得到,dp[i]=max(dp[i-2]+nums[i],dp[i-1]) (2020.3.22 更新了代码)
// Max[i]=max(nums[i-2]+nums[i],nums[i-1])
public int rob(int[] nums) {
if(nums==null || nums.length<=0) return 0;
int[] dp=new int[nums.length];
dp[0]=nums[0];
for(int i=1;i<nums.length;i++){
dp[i]=Math.max(i>=2?dp[i-2]+nums[i]:nums[i],dp[i-1]);
}
return dp[nums.length-1];
}
时间空间都是 O(N),需要注意边界条件
解法二
空间复杂度的优化
// Max[i]=max(pre+nums[i],cur);
public int rob(int[] nums) {
if(nums==null||nums.length<=0){
return 0;
}
int pre= 0; //前一天
int cur= 0; //当天,其实就是为了保存前后两天的 dp[i]
for (int i=0;i<nums.length;i++) {
int temp=cur;
cur=Math.max(pre+nums[i],cur);
//向后走
pre=temp;
}
return cur;
}
213. 打家劫舍 II
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都围成一圈,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入:[2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入:[1,2,3,1]
输出:4
解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
解法一
与上一题相比房屋都围成一圈了,其实围成一圈也就说明nums[0]和nums[len-1]不能同时偷,所以就可以分两种情况分别求最大值,然后求最终的最大值
public int rob(int [] nums){
if(nums==null||nums.length<=0){
return 0;
}
if(nums.length==1){
return nums[0];
}
if(nums.length==2){
return Math.max(nums[0],nums[1]);
}
int n=nums.length;
return Math.max(rob(nums,1,n),rob(nums,0,n-1));
}
public int rob(int[] nums,int start,int end) {
int pre=0; //前一家最大值
int cur=0; //当前最大值
for (int i=start;i<end;i++) {
int temp=cur;
cur=Math.max(pre+nums[i],cur);
pre=temp;
}
return cur;
}
64. 最小路径和
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
很经典的 DP 题。
递推公式:dp[i][j] = grid[i][j] + Math.min(dp[i-1][j],dp[i][j-1])
dp[i] [j] 为每个格子到左上角最短路径 ,每个格子到左上角的最小距离等于,左边格子最小值和上边格子最小值的最小值加上当前格子的值。
public int minPathSum(int[][] grid) {
int[][] dp=new int[grid.length][grid[0].length];
for (int i=0;i<grid.length;i++) {
for (int j=0;j<grid[0].length;j++) {
//第一行
if(i==0 && j!=0){
dp[i][j]=grid[i][j]+dp[i][j-1];
}else if(i!=0 && j==0){
dp[i][j]=grid[i][j]+dp[i-1][j];
}else if(i!=0 && j!=0){
dp[i][j]=grid[i][j]+Math.min(dp[i-1][j],dp[i][j-1]);
}else{
dp[i][j]=grid[i][j];
}
}
}
return dp[grid.length-1][grid[0].length-1];
}
UPDATE: 2020.7.20
写下面的 path-sum-three-ways 的时候看了这题之前的代码,发现写的不太好,一堆 if-else,重写下
func minPathSum(grid [][]int) int {
var m = len(grid)
var n = len(grid[0])
var dp = make([][]int, m)
for i := 0; i < m; i++{
dp[i] = make([]int, n)
}
dp[0][0] = grid[0][0]
for i := 1; i < m; i++{
dp[i][0] = dp[i-1][0] + grid[i][0]
}
for j := 1; j < n; j++{
dp[0][j] = dp[0][j-1] + grid[0][j];
}
for i := 1; i < m; i++{
for j := 1; j < n; j++{
dp[i][j] = grid[i][j] + Min(dp[i-1][j], dp[i][j-1])
}
}
return dp[m-1][n-1]
}
func Min(a, b int) int{
if a > b{
return b
}
return a
}
Path sum: three ways
The minimal path sum in the 5 by 5 matrix below, by starting in any cell in the left column and finishing in any cell in the right column, and only moving up, down, and right, is indicated in red and bold; the sum is equal to 994.
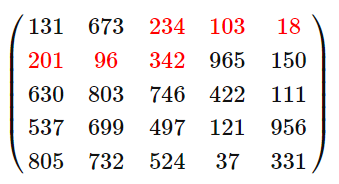
Find the minimal path sum from the left column to the right column in matrix.txt (right click and “Save Link/Target As…”), a 31K text file containing an 80 by 80 matrix.
解法一
来源 https://leetcode-cn.com/circle/discuss/BNvWBP/ 从这里看见 qc 大佬贴了出处,所以特地注册了这个网站试了下,这个网站还是挺有意思的,只验证答案,时间复杂度啥的都不管
和上面的最小路径和很类似,但是这里起点和终点都不确定,而且有 3 个方向可以选择,所以这里我们可以遍历 2 次,dp[i][j]代表从第一列到当前matrix[i][j]的最小路径和,先统计单纯的向上或者向下的最小值,然后再统计相反的方向的值,总之要保证 3 个方向的值都是计算过的
import java.util.*;
import java.io.*;
//https://projecteuler.net/problem=82 answer:260324
public class PathSum_threeWays_projecteuler{
public static void main(String[] args) throws Exception{
BufferedReader reader = new BufferedReader(new FileReader("/usr/p082_matrix.txt"));
int index = 0;
int m = 80, n = 80;
int[][] matrix = new int[m][n];
while (index < 80) {
String[] line = reader.readLine().split(",");
for (int j = 0; j < 80; j++) {
matrix[index][j] = Integer.valueOf(line[j]);
}
index++;
}
int INF = 0x3f3f3f3f;
int[][] dp = new int[m][n];
for (int j = 0; j < m; j++) {
dp[j][0] = matrix[j][0];
}
for (int j = 1; j < m; j++) {
//首先只考虑向右走和向下走
for (int i = 0; i < m; i++) {
if (i==0){ //第一行,只能从左边转移
dp[i][j] = matrix[i][j] + dp[i][j-1];
}else{ //从左边或者上边转移
dp[i][j] = matrix[i][j] + Math.min(dp[i][j-1], dp[i-1][j]);
}
}
for (int i = m-1; i >= 0; i--) {
//三目写的太长看着挺不舒服。..
//dp[i][j] = i==m-1?dp[i][j]:Math.min(dp[i][j], matrix[i][j]+dp[i+1][j]);
if (i<m-1) { //从下面转移和从上/左面转移的最小值
dp[i][j] = Math.min(dp[i][j], matrix[i][j]+dp[i+1][j]);
}
//最后一行,只能从左边或者上面转移,也是就是第一个循环的值
//dp[i][j] = dp[i][j]
}
}
int res = INF;
for (int i = 0; i < m; i++) {
res = Math.min(res, dp[i][m-1]);
}
System.out.println(res);
}
}
一开始写了个 3 目,改了半天的 bug,发现是 3 目和前面的值混到一起了。
62. 不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?

**说明:**m 和 n 的值均不超过 100。
示例 1:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向右 -> 向下
2. 向右 -> 向下 -> 向右
3. 向下 -> 向右 -> 向右
示例 2:
输入:m = 7, n = 3
输出:28
动态规划解法
这题算是我第一道自己做出来的 DP 题了,虽然和上面的一题一样的思路,但是还是挺开心的
public int uniquePaths(int m, int n) {
if(m<0||n<0){
return 0;
}
int[][] dp=new int[n][m];
for (int i=0;i<n;i++) {
for (int j=0;j<m;j++) {
if(i==0&&j!=0){
dp[i][j]=1;
}else if(j==0 && i!=0){
dp[i][j]=1;
}else if(j!=0&&i!=0){
dp[i][j]=dp[i][j-1]+dp[i-1][j];
}else{
dp[i][j]=1;
}
}
}
return dp[n-1][m-1];
}
时间复杂度O(m*n),空间复杂度O(m*n)可以看出来完全是按照前一题的模板来的,代码写的不好,可以把 if-else 合并起来,这题空间复杂度其实还可以优化成 O(m) 或 O(n) 的,按行来向下走
空间复杂度优化

public static int uniquePaths2(int m, int n) {
if(m<0||n<0){
return 0;
}
int[] dp=new int[n];
Arrays.fill(dp,1); //第一行,第一列均为 1
for (int i=1;i<m;i++) { //一行一行向下走
for (int j=1;j<n;j++) {
//这里的 dp[j] 和 dp[j-1] 分别就代表了 上边 和 左边的元素
dp[j]=dp[j]+dp[j-1]; //求每一行每个元素的 dp 值
}
}
return dp[n-1]; //最后一行最后一个 dp 值就是结果
}
组合数公式
这题其实就是我们初中还是高中学的排列组合的问题,机器人一共走m+n-2 步,向下会走m-1 步,向下会走n-1 步,所以实际上就是求一个组合数的结果 C(n-1,m+n-2) ,
public int uniquePaths(int m, int n) {
if(m<0||n<0){
return 0;
}
int step=m+n-2;
int down=n-1;
long res=1;
for (int i=1;i<=down;i++) {
res=res*(step-down+i)/i; //递推
}
return (int)res;
}
63. 不同路径 II
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?

网格中的障碍物和空位置分别用 1 和 0 来表示。
**说明:**m 和 n 的值均不超过 100。
示例 1:
输入:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
输出:2
解释:
3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
解法一
看到这种路径的题,首先想到的可能是递归回溯
//dfs 回溯 , TLE
private int[][] direction={{0,1},{1,0}};
private int count=0;
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
if (obstacleGrid==null || obstacleGrid.length<=0 || obstacleGrid[0][0]==1) {
return 0;
}
boolean[][] visit=new boolean[obstacleGrid.length][obstacleGrid[0].length];
dfs(obstacleGrid,visit,0,0);
return count;
}
public void dfs(int[][] obstacleGrid,boolean[][] visit,int x,int y) {
//!=1 是为了 coner case
if (x==obstacleGrid.length-1 && y==obstacleGrid[0].length-1 && obstacleGrid[x][y]!=1) {
count++;
return;
}
for (int i=0;i<direction.length;i++) {
int nx=x+direction[i][0];
int ny=y+direction[i][1];
if (nx<obstacleGrid.length && ny<obstacleGrid[0].length && !visit[nx][ny] && obstacleGrid[nx][ny] !=1) {
visit[nx][ny]=true;
dfs(obstacleGrid,visit,nx,ny);
visit[nx][ny]=false;
}
}
}
结果很惨,TLE 了,只跑了不到一半的 case 就 TLE 了
解法二
动态规划的解法,其实和上面一题是一样的,只不过需要注意障碍物位置的 dp 值
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
if (obstacleGrid==null || obstacleGrid.length<=0 || obstacleGrid[0][0]==1) {
return 0;
}
int[][] dp=new int[obstacleGrid.length][obstacleGrid[0].length];
for (int i=0;i<obstacleGrid.length;i++) {
for (int j=0; j<obstacleGrid[0].length;j++) {
if (obstacleGrid[i][j]==1) {
dp[i][j]=0;
}else if (i==0 && j==0) {
dp[0][0]=1;
}else if(i==0 && j!=0){
dp[0][j]=dp[0][j-1];
}else if (j==0 && i!=0) {
dp[i][0]=dp[i-1][0];
}else{
dp[i][j]=dp[i-1][j]+dp[i][j-1];
}
}
}
return dp[obstacleGrid.length-1][obstacleGrid[0].length-1];
}
和上面一样也可以进行空间上的优化
//一维 dp
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
if (obstacleGrid==null || obstacleGrid.length<=0 || obstacleGrid[0][0]==1) {
return 0;
}
//以行为单位向下走
int[] dp=new int[obstacleGrid[0].length];
dp[0]=1;
for (int i=0;i<obstacleGrid.length;i++) {
for (int j=0; j<obstacleGrid[0].length;j++) {
if (obstacleGrid[i][j]==1) {
dp[j]=0;
}else if(i==0 && j!=0){ //第一行
dp[j]=dp[j-1];
}else if(i!=0 && j!=0){
dp[j]=dp[j]+dp[j-1];
}
//每一行第一列的 dp[j]=dp[j], 和上一行的第一列保持一致就行
}
}
return dp[obstacleGrid[0].length-1];
}
UPDATE: 2020.7.6
想对简洁的做法
func uniquePathsWithObstacles(grid [][]int) int {
var m = len(grid)
var n = len(grid[0])
var dp = make([][]int, m+1)
for i := 0; i <= m; i++ {
dp[i] = make([]int, n+1)
}
dp[0][1] = 1 //初始值
for i := 1; i <= m; i++ {
for j := 1; j <= n; j++ {
if grid[i-1][j-1] != 1 {
dp[i][j] = dp[i-1][j] + dp[i][j-1]
}
}
}
return dp[m][n]
}
576. 出界的路径数
给定一个 m × n 的网格和一个球。球的起始坐标为 (i,j) ,你可以将球移到相邻的单元格内,或者往上、下、左、右四个方向上移动使球穿过网格边界。但是,你最多可以移动 N 次。找出可以将球移出边界的路径数量。答案可能非常大,返回 结果 mod 109 + 7 的值。
示例 1:
输入:m = 2, n = 2, N = 2, i = 0, j = 0
输出:6
解释:
示例 2:
输入:m = 1, n = 3, N = 3, i = 0, j = 1
输出:12
解释:
说明:
- 球一旦出界,就不能再被移动回网格内。
- 网格的长度和高度在 [1,50] 的范围内。
- N 在 [0,50] 的范围内。
解法一
首先写出来的解法,自顶向下,记忆化递归
int[][] dir={{0,1},{1,0},{-1,0},{0,-1}};
int mod=(int)1e9+7;
Long[][][] dp=null;
public int findPaths(int m, int n, int N, int i, int j) {
dp=new Long[m][n][N+1];
return (int)(dfs(m,n,i,j,N)%mod);
}
public long dfs(int m,int n,int x,int y,int k){
if(k==0) return 0;
if(dp[x][y][k]!=null){
return dp[x][y][k];
}
long count=0;
for(int i=0;i<dir.length;i++){
int nx=x+dir[i][0];
int ny=y+dir[i][1];
if(!valid(m,n,nx,ny)){
count++;
continue;
}
count=(count+dfs(m,n,nx,ny,k-1))%mod;
}
return dp[x][y][k]=(count)%mod;
}
public boolean valid(int m,int n,int x,int y){
return x>=0 && x<m && y>=0 && y<n;
}
有一点需要注意,这里不需要 visit,因为有 K 的限制,不用担心死循环,感觉加了 visit 反而会错?
解法二
整体上来说还是属于比较简单的动态规划,至少递推方程好想
//自底向上递推
public int findPaths(int m, int n, int N, int i, int j) {
int mod=(int)1e9+7;
//群里偷学到的
int[] dir={0,1,0,-1,0};
long[][][] dp=new long[m][n][N+1];
for (int k=1;k<=N;k++) { //想想 K 为什么在最外层
for (int r=0;r<m;r++) {
for (int c=0;c<n;c++) {
for (int d=0;d<4;d++) {
int nx=r+dir[d];
int ny=c+dir[d+1];
if(nx<0 || ny<0 || nx>=m ||ny>=n){
dp[r][c][k]++;
}else{
dp[r][c][k]=(dp[r][c][k]+dp[nx][ny][k-1])%mod;
}
}
//提前结束,只需要 i,j,N 就行了(貌似没有快多少)
if(k==N && r==i && c==j){
return (int)(dp[i][j][N]);
}
}
}
}
//return (int)(dp[m-1][n-1][N]); md 一开始返回错了,看了半天
return 0;
}
K 放在最外层的原因其实很容易想到,我们求某一个点的时候,我们需要周围 4 个方向的K-1的值,这些值必须是已经计算过的,所以 K 肯定是要放在最外层的
688. “马”在棋盘上的概率
已知一个 NxN 的国际象棋棋盘,棋盘的行号和列号都是从 0 开始。即最左上角的格子记为 (0, 0),最右下角的记为 (N-1, N-1)。
现有一个 “马”(也译作 “骑士”)位于 (r, c) ,并打算进行 K 次移动。
如下图所示,国际象棋的 “马” 每一步先沿水平或垂直方向移动 2 个格子,然后向与之相垂直的方向再移动 1 个格子,共有 8 个可选的位置。

现在 “马” 每一步都从可选的位置(包括棋盘外部的)中独立随机地选择一个进行移动,直到移动了 K 次或跳到了棋盘外面。
求移动结束后,“马” 仍留在棋盘上的概率。
示例:
输入:3, 2, 0, 0
输出:0.0625
解释:
输入的数据依次为 N, K, r, c
第 1 步时,有且只有 2 种走法令 “马” 可以留在棋盘上(跳到(1,2)或(2,1))。对于以上的两种情况,各自在第 2 步均有且只有 2 种走法令 “马” 仍然留在棋盘上。
所以 “马” 在结束后仍在棋盘上的概率为 0.0625。
注意:
N的取值范围为 [1, 25]K的取值范围为 [0, 100]- 开始时,“马” 总是位于棋盘上
错误解法一
首先采用了和上一题类似做法,明显是不行的
//小数据可以过,大数据过不了
//K[0,100] 直接 8^100 就爆了,所以肯定不能像上面那样求,dp 得存概率
public double knightProbability(int N, int K, int r, int c) {
int[][] dir={{-2,-1},{-2,1},{-1,2},{1,2},{2,1},{2,-1},{1,-2},{-1,-2}};
int[][][] dp=new int[N][N][K+1];
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
//这题如果反着求出界路径就错了,得正向求
dp[i][j][0]=1;
}
}
for(int k=1;k<=K;k++){
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
for(int d=0;d<dir.length;d++){
int nx=i+dir[d][0];
int ny=j+dir[d][1];
if(nx>=0 && nx<N && ny>=0 && ny<N){
dp[i][j][k]+=(dp[nx][ny][k-1]);
}
}
}
}
}
return dp[r][c][K]/Math.pow(8,K);
}
多说一点,这里为什么不和上面一样,算出界的路径数,然后用
8^K减去出界数量,然后除以8^K?其实主要是出界的这里并不好算,这里要求的是概率,出界的路径并不能完全包含出界的方式(可以理解为出界后仍然可以走)
解法二
标准的 dp 解法,注意概率的计算就行了
//DP 存概率 AC 解法
public double knightProbability(int N, int K, int r, int c) {
int[][] dir={{-2,-1},{-2,1},{-1,2},{1,2},{2,1},{2,-1},{1,-2},{-1,-2}};
double[][][] dp=new double[N][N][K+1];
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
dp[i][j][0]=1;
}
}
for(int k=1;k<=K;k++){
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
for(int d=0;d<dir.length;d++){
int nx=i+dir[d][0];
int ny=j+dir[d][1];
if(nx>=0 && nx<N && ny>=0 && ny<N){
//md,一开始不知道为啥想到求独立事件 P(A U B) 上去了
//但是其实两者并不是独立事件,是互斥事件直接 P(A)+P(B) 就行了
dp[i][j][k]+=(dp[nx][ny][k-1])/8;
}
}
//提前返回
if(i==r && j==c && k==K){
return dp[i][j][k];
}
}
}
}
return dp[r][c][K];
}
解法三
记忆化的方式,其实会比上面递推的会快一点,上面递推的会有很多无用状态
//自顶向上
Double[][][] dp=null;
int[][] dir={{-2,-1},{-2,1},{-1,2},{1,2},{2,1},{2,-1},{1,-2},{-1,-2}};
public double knightProbability(int N, int K, int r, int c) {
dp=new Double[N][N][K+1];
return dfs(N,K,r,c);
}
public double dfs(int N,int k,int x,int y){
if(k==0) return 1.0;
if(dp[x][y][k]!=null){
return dp[x][y][k];
}
double p=0;
for (int i=0;i<dir.length;i++) {
int nx=x+dir[i][0];
int ny=y+dir[i][1];
if(nx>=0 && nx<N && ny>=0 && ny<N){
p+=dfs(N,k-1,nx,ny)/8;
}
}
return dp[x][y][k]=p;
}
935. 骑士拨号器
国际象棋中的骑士可以按下图所示进行移动:
 .
. 
这一次,我们将 “骑士” 放在电话拨号盘的任意数字键(如上图所示)上,接下来,骑士将会跳 N-1 步。每一步必须是从一个数字键跳到另一个数字键。
每当它落在一个键上(包括骑士的初始位置),都会拨出键所对应的数字,总共按下 N 位数字。
你能用这种方式拨出多少个不同的号码?
因为答案可能很大,所以输出答案模 10^9 + 7。
示例 1:
输入:1
输出:10
示例 2:
输入:2
输出:20
示例 3:
输入:3
输出:46
提示:
1 <= N <= 5000
解法一
先上一个极其粗糙的解法,也是最开始的解法
int[][] dir={{-2,-1},{-2,1},{-1,2},{1,2},{2,1},{2,-1},{1,-2},{-1,-2}};
int mod=(int)1e9+7;
Integer[][][] dp=null;
public int knightDialer(int N) {
int[][] grid={{1,2,3},{4,5,6},{7,8,9},{-1,0,-1}};
int res=0;
dp=new Integer[4][3][N];
for(int i=0;i<grid.length;i++){
for(int j=0;j<grid[0].length;j++){
if(grid[i][j]!=-1){
res=(res+dfs(grid,i,j,N-1))%mod;
}
}
}
return res;
}
public int dfs(int[][] grid,int x,int y,int N){
if(N==0) return 1;
if(dp[x][y][N]!=null) return dp[x][y][N];
int res=0; //一开始赋值成 1 了。从当前位置起跳,所以当前位置不应该有初始值
for(int i=0;i<dir.length;i++){
int nx=x+dir[i][0];
int ny=y+dir[i][1];
if(valid(grid,nx,ny)){
res=(res+dfs(grid,nx,ny,N-1))%mod;
}
}
return dp[x][y][N]=res;
}
public boolean valid(int[][] grid,int x,int y){
return x>=0 && y>=0 && x<grid.length && y<grid[0].length && grid[x][y]!=-1;
}
解法二
小巧精致的解法
int mod=(int)1e9+7;
Integer[][] dp=null;
public int knightDialer(int N) {
//直接看图建立对应关系
int[][] next={{4,6},{6,8},{7,9},{4,8},{0,3,9},{},{0,1,7},{2,6},{1,3},{2,4}};
int res=0;
dp=new Integer[10][N];
for(int i=0;i<=9;i++){
res=(res+dfs(i,N-1,next))%mod;
}
return res;
}
public int dfs(int num,int N,int[][] next){
if(N==0) return 1;
if(dp[num][N]!=null) return dp[num][N];
int res=0; //注意别写成 1 了
for(int i=0;i<next[num].length;i++){
res=(res+dfs(next[num][i],N-1,next))%mod;
}
return dp[num][N]=res;
}
解法三
递推的方式
//递推的方式
public int knightDialer(int N) {
//next[i]: i 下一步能跳到的位置
int[][] next={{4,6},{6,8},{7,9},{4,8},{0,3,9},{},{0,1,7},{2,6},{1,3},{2,4}};
int[][] dp=new int[N][10];
Arrays.fill(dp[0],1); //base dp[0]
int mod=(int)1e9+7;
int res=0;
for (int i=1;i<N;i++) {
for (int num=0;num<=9;num++) {
for (int j=0;j<next[num].length;j++) {
dp[i][num]=(dp[i][num]+dp[i-1][next[num][j]])%mod;
}
}
}
for(int i=0;i<=9;i++) res=(res+dp[N-1][i])%mod;
return res;
}
303. 区域和检索 - 数组不可变
给定一个整数数组 nums,求出数组从索引 i 到 j (i ≤ j) 范围内元素的总和,包含 i, j 两点。
示例:
给定 nums = [-2, 0, 3, -5, 2, -1],求和函数为 sumRange()
sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3
说明:
- 你可以假设数组不可变。
- 会多次调用 sumRange 方法。
解法一
这题其实一开始就是想的缓存一下之前调用产生的值,没有理解到这题的要点。
class NumArray {
private int[] sums=null;
public NumArray(int[] nums) {
if (nums!=null && nums.length>0) {
sums=new int[nums.length];
sums[0]=nums[0];
for (int i=1;i<sums.length;i++) {
sums[i]=sums[i-1]+nums[i];
}
}
}
public int sumRange(int i, int j) {
if(i==0){
return sums[j];
}
return sums[j]-sums[i-1];
}
}
/**
* Your NumArray object will be instantiated and called as such:
* NumArray obj = new NumArray(nums);
* int param_1 = obj.sumRange(i,j);
*/
这题关键有两个地方,一个是 sumRange(i , j) = sumRange(0, j)-sumRange(0, i-1) ,另一个关键就是在构造器里面将所有的 sumRange(0 , i) 给预先求出来,这样在后面的调用时时间复杂度就是O(1)的了。
这里求sumRange(0, i)的过程就是一个很简单的 dp.
413. 等差数列划分
如果一个数列至少有三个元素,并且任意两个相邻元素之差相同,则称该数列为等差数列。
例如,以下数列为等差数列:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
以下数列不是等差数列。
1, 1, 2, 5, 7
数组 A 包含 N 个数,且索引从 0 开始。数组 A 的一个子数组划分为数组 (P, Q),P 与 Q 是整数且满足 0<=P<Q<N 。
如果满足以下条件,则称子数组 (P, Q) 为等差数组:
元素 A[P], A[p + 1], …, A[Q - 1], A[Q] 是等差的。并且 P + 1 < Q 。
函数要返回数组 A 中所有为等差数组的子数组个数。
示例:
A = [1, 2, 3, 4]
返回:3, A 中有三个子等差数组:[1, 2, 3], [2, 3, 4] 以及自身 [1, 2, 3, 4]。
dp 的题啊,答案一看就明白,就是自己想不到。
public int numberOfArithmeticSlices(int[] A) {
if(A.length<3){
return 0;
}
//dp[i]=dp[i-1]+1;
int []dp=new int[A.length]; //以 A[i] 结尾的等差数列有多少个
for (int i=2;i<A.length;i++) {
if(A[i]-A[i-1]==A[i-1]-A[i-2]){
dp[i]=dp[i-1]+1;
}
}
int res=0;
for (int i=0;i<dp.length;i++) {
res+=dp[i];
}
return res;
}
就是没想到要对以当前元素结尾的动态数组数量做 dp,当然上面的做法的空间还可以优化成 O(1) 的
public int numberOfArithmeticSlices2(int[] A) {
if(A.length<3){
return 0;
}
//dp[i]=dp[i-1]+1;
int dp=0;
int res=0;
for (int i=2;i<A.length;i++) {
if(A[i]-A[i-1]==A[i-1]-A[i-2]){
dp=dp+1;
res+=dp;
}else{
dp=0;
}
}
return res;
}
只需要根据上一次的 dp 值更新就行,如果 break 等差数列,就置为 0
343. 整数拆分
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
示例 1:
输入:2
输出:1
解释:2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入:10
输出:36
解释:10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
说明: 你可以假设 n 不小于 2 且不大于 58。
解法一
别问,问就是暴力

递推式: F(n) = max {i * F(n - i)},i = 1,2,...,n - 1
穷举每一种分解情况,求最大值
public static int integerBreak(int n) {
//递归出口
if (n==2) {
return 1;
}
int res=-1;
for (int j=1;j<n;j++) {
//第一个 Max 求最大值,第二个 Max 主要是为了考虑 只分两个数就是最大值的情况(<=7 的情况)
res=Math.max(res, Math.max((n-j)*j,integerBreak(n-j)*j));
}
return res;
}
需要注意的就是第二个 Max 别忘了只分为两个数就到达最大值的情况,比如 n<=7 的时候,integerBreak(n-j)*j) 至少是三个,下面的 DP 也是一样的要注意别忘了两个数的情况
递归的时间复杂度应该是O(N!) ,后面的 case 会超时,其实很明显,递归过程中会有很多的重复计算所以可以采用记忆化递归缓存一下之前的值。
private Integer[] cache=null;
//只顶向下,记忆化递归
public int integerBreak(int n) {
cache=new Integer[n+1];
return breakInteger(n);
}
public int breakInteger(int n) {
if (cache[n]!=null) {
return cache[n];
}
//递归出口
if (n==2) {
return 1;
}
int res=-1;
for (int j=1;j<n;j++) {
res=Math.max(res, Math.max((n-j)*j,breakInteger(n-j)*j));
}
cache[n]=res;
return res;
}
这样的解法是可以 AC 的,缓存之前计算的结果,避免了重复的计算
解法二
动态规划,结合上面的递归得到递推方程
dp[i] = max(dp[i],max(dp[ i-j ] * j ,(i-j) * j));
public static int integerBreak2(int n) {
if (n==2) {
return 1;
}
int [] dp=new int[n+1];
dp[2]=1; //0,1 不考虑
for (int i=3;i<=n;i++) {
for (int j=1;j<i;j++) {
dp[i]=Math.max(dp[i],Math.max(dp[i-j]*j,(i-j)*j));
}
}
return dp[n];
}
解法三
打板找规律,笔试的时候能直接一眼看出来规律的肯定优先找规律了
public static int integerBreak3(int n) {
int[] base={1,2,4,6,9,12};
if(n<=7){
return base[n-2];
}
int[] dp=new int[n+1];
dp[2]=base[0];
dp[3]=base[1];
dp[4]=base[2];
dp[5]=base[3];
dp[6]=base[4];
dp[7]=base[5];
for (int i=8;i<=n;i++) {
dp[i]=dp[i-3]*3; //N>7 之后 dp[N]=dp[N-3]*3
}
return dp[n];
}
解法四
数学分析,其实分析一下会发现,只有 2 和 3 是分解后值比本身还要小的,4 分解后相等,这样一分析,从整体上来看其实就清楚了,只要分到 2 或者 3 的时候就不再分就行了,此时的值一定是最大值,如果 2,3 继续分值就会减小
public int integerBreak(int n) {
int[] base={1,2,4};
if(n<=4){
return base[n-2];
}
int res=1;
while(n>=5){
res*=3;
n-=3;
}
res*=n;
return res;
}
取模写法,这里其实涉及到取模的一个规则,(a*b)%mod=(a%mid * b%mid) % mod
public int cuttingRope(int n) {
if(n<=3) return n-1;
long res=1;
while(n>=5){
n-=3;
res=(res*3)%1000000007;
}
return (int)(res*n%1000000007);
}
279. 完全平方数
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4.
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9.
解法一
动态规划,不容易啊,自己推出了 DP 方程,没看答案,其实也借鉴了上一题的思路
dp[i] =min(dp[i],dp[i-j*j]+1)
其实也是将整数拆分,不过拆分的时候按照 完全平方数 来拆分,完全平方数的肯定是 1 所以最后要加个 1
public static int numSquares(int n) {
int[] dp=new int[n+1];
dp[0]=0;
for (int i=1;i<=n;i++) {
dp[i]=Integer.MAX_VALUE; //dp[i] 初始化
for (int j=1;i>=j*j;++j){
dp[i]=Math.min(dp[i],dp[i-j*j]+1);
}
}
return dp[n];
}
50%左右,看了下时间复杂度应该是 O(N^1.5) 还是挺高的(评论区用 Py 的都超时了)
解法二
BFS,将数字按照完全平方数连接为一个图,然后 BFS 求一个从 n 到 0 的最短的路径
public static int numSquares(int n) {
Queue<Pair> queue=new LinkedList<>();
boolean[] visit=new boolean[n+1];
queue.add(new Pair(n,0));
visit[n]=true;
while(!queue.isEmpty()){
Pair pair=queue.poll();
int num=pair.num;
int step=pair.step;
if (num==0) {
return step;
}
for (int i=1;i*i<=num;i++) {
int temp=num-i*i;
if (!visit[temp]) {
queue.add(new Pair(temp,step+1));
visit[temp]=true;
}
}
}
return -1;
}
static class Pair{
public int step;
public int num;
public Pair(int num,int step){
this.num=num;
this.step=step;
}
}
这题最快的做法应该是利用 四平方和定理 我也不太清楚,所以暂时先不研究这种做法
91. 解码方法
一条包含字母 A-Z 的消息通过以下方式进行了编码:
'A' -> 1
'B' -> 2
...
'Z' -> 26
给定一个只包含数字的非空字符串,请计算解码方法的总数。
示例 1:
输入:"12"
输出:2
解释:它可以解码为 "AB"(1 2)或者 "L"(12)。
示例 2:
输入:"226"
输出:3
解释:它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。
解法一
哇,这题我吐了,好不容易看出来了递推公式,被边界给整死了。面向测试用例编程。
public static int numDecodings(String s) {
if (s.startsWith("0")) {
return 0;
}
int[] s_nums=new int[s.length()];
for (int i=0;i<s.length();i++) {
s_nums[i]=Integer.valueOf(s.charAt(i)-48);
}
int[] dp =new int[s_nums.length];
Arrays.fill(dp,1);
dp[0]=1;
int res=1;
for (int j=1;j<s_nums.length;j++) {
if(s_nums[j]==0 && s_nums[j-1]==0 || (s_nums[j]==0 && s_nums[j-1]>2)){
//直接 return
return 0;
}
if( s_nums[j]==0 || s_nums[j-1]==0 || (j<s_nums.length-1 &&s_nums[j+1]==0)){
//为了处理 12120 这种情况
res*=dp[j-1];
continue;
}
if(s_nums[j-1]*10+s_nums[j]<=26){
if(j==1){
dp[j]=2;
}else{
dp[j]=dp[j-1]+dp[j-2];
}
}else{
//划分点。
res*=dp[j-1];
dp[j-1]=1;
dp[j]=1;
}
}
//最后一段
res*=dp[s_nums.length-1];
return res;
}
首先要推出这题的递推公式,我也是在纸上画了半天才看出来,如果这个数组前后两个元素之和都是小于 26 的那么这一段的编码方式就是一个斐波拉契数列 ,也就是 dp[i]=dp[i-1]+dp[i-2]
80%左右,这题其实一开始并不是这样做的,我觉得我开始的思路还是挺好的,将字符串分段,当前一个和后一个无法合并的时候就作为一个分界点,最后将每一段的编码方式相乘就是结果了。
但是 !!! 我忽略了 0 这个东西了,这题后面给的 case 里面都是带有 0 的!!!!处理这个边界处理了一上午终于跑过了。代码也没什么好说的,写的太烂了,这种代码没啥意义,都是走一步看一步。
解法二
public static int numDecodings2(String s) {
if (s.startsWith("0")) {
return 0;
}
int[] s_nums=new int[s.length()];
for (int i=0;i<s.length();i++) {
s_nums[i]=Integer.valueOf(s.charAt(i)-48);
}
int[] dp=new int[s.length()+1];
dp[0]=1;
dp[1]=1;
for (int i=2;i<=s.length();i++) {
int a=s_nums[i-1];
if(a!=0){
//到这里 dp[i]==0, 没有初始化,默认就是 0
//其实等价于 dp[i]=dp[i-1], 延续前一个字符的状态
dp[i]+=dp[i-1];
}
if(s_nums[i-2]==0){
//如果前前一个字符为 0 那么就不用 dp 了,保持 i-1 的状态就 OK
continue;
}
//前前一个字符和
int b=s_nums[i-2]*10+s_nums[i-1];
if(b<=26){
dp[i]+=dp[i-2]; //上下这两个 dp 必须执行一个否则最后就 return 0
}
}
return dp[s_nums.length];
}
这种写法就清晰多了,分析各种情况,dp 代表截至字符的编码方式
💬 s_num[i-1]!=0 && s_num[i-2]!=0 && s_num[i-2]+s_num[i-1] <=26
类似于 112 这样的,这就是正常 dp 的情况符合斐波拉契数列
💬 s_num[i-1]==0 && s_num[i-2]!=0 && s_num[i-2]+s_num[i-1] <=26
类似于 102 这样的,这样就直接继承 dp[i-2] 的状态就行了,相当于dp[i]=dp[i-2]
💬 s_num[i-1]!=0 && s_num[i-2]!=0 && s_num[i-2]+s_num[i-1] >26
类似于 132 这样的,这样就直接继承 dp[i-2] 的状态就行了,相当于dp[i]=dp[i-2]
💬 s_num[i-1]!=0 && s_num[i-2]==0 && s_num[i-2]+s_num[i-1] <=26
类似于 **…012 **这样的,dp[i]=dp[i-1]
💬 s_num[i-1]==0 && s_num[i-2]==0 或者s_num[i-1]==0 && s_num[i-2]!=0 && s_num[i-2]+s_num[i-1]>26
类似于** 00** 和** 30** 这样的, 这样就代表这个字符串无法编码了 dp[i]=0 最后返回的就是 0
面试题 46. 把数字翻译成字符串
给定一个数字,我们按照如下规则把它翻译为字符串:0 翻译成 “a” ,1 翻译成 “b”,……,11 翻译成 “l”,……,25 翻译成 “z”。一个数字可能有多个翻译。请编程实现一个函数,用来计算一个数字有多少种不同的翻译方法。
示例 1:
输入:12258
输出:5
解释:12258 有 5 种不同的翻译,分别是"bccfi", "bwfi", "bczi", "mcfi"和"mzi"
提示:
0 <= num < 231
解法一
代码比较丑,逻辑还是比较清晰,其实这题算是上面 91. 解码方法的弱化没有了 0 的限制,0 是合法的数字,这样就舒服多了,上面解码方法确实做的脑壳疼
public int translateNum(int num) {
String s=String.valueOf(num);
int len=s.length();
if(len==0 || len==1) return 1;
int[] dp=new int[len];
//1 2 2 5 8
//1 2 3 5 5
dp[0]=1;
dp[1]=Integer.valueOf(s.substring(0,2))>25?1:2;
for(int i=2;i<len;i++){
int pre=Integer.valueOf(s.charAt(i-1))-48;
int cur=Integer.valueOf(s.charAt(i))-48;
if(pre!=0 && Integer.valueOf(pre*10+cur)<=25){
dp[i]=dp[i-1]+dp[i-2];
}else{
dp[i]=dp[i-1];
}
}
return dp[len-1];
}
5375. 恢复数组
某个程序本来应该输出一个整数数组。但是这个程序忘记输出空格了以致输出了一个数字字符串,我们所知道的信息只有:数组中所有整数都在 [1, k] 之间,且数组中的数字都没有前导 0 。
给你字符串 s 和整数 k 。可能会有多种不同的数组恢复结果。
按照上述程序,请你返回所有可能输出字符串 s 的数组方案数。
由于数组方案数可能会很大,请你返回它对 10^9 + 7 取余 后的结果。
示例 1:
输入:s = "1000", k = 10000
输出:1
解释:唯一一种可能的数组方案是 [1000]
示例 2:
输入:s = "1000", k = 10
输出:0
解释:不存在任何数组方案满足所有整数都 >= 1 且 <= 10 同时输出结果为 s 。
示例 3:
输入:s = "1317", k = 2000
输出:8
解释:可行的数组方案为 [1317],[131,7],[13,17],[1,317],[13,1,7],[1,31,7],[1,3,17],[1,3,1,7]
示例 4:
输入:s = "2020", k = 30
输出:1
解释:唯一可能的数组方案是 [20,20] 。 [2020] 不是可行的数组方案,原因是 2020 > 30 。 [2,020] 也不是可行的数组方案,因为 020 含有前导 0 。
示例 5:
输入:s = "1234567890", k = 90
输出:34
提示:
- 1 <= s.length <= 10^5.
- s 只包含数字且不包含前导 0 。
- 1 <= k <= 10^9.
解法一
24th 双周赛的 T4,其实 dp 的状态转换还是想出来了,我想的是从左向右,但是细节没理清楚,瞄了一眼评论区,发现从右往左比较简单
public int numberOfArrays(String s, int k) {
int mod=1_000_000_000 + 7;
int[] dp=new int[s.length()+1];
dp[0]=1;
//dp[i]=dp[i-1]+dp[i-2]+...+dp[0];
for (int i=1;i<=s.length();i++) {
for (int j=i-1;j>=0 && i-j<=9;j--) {
if(s.charAt(j)!='0' && valid(s,j,i,k)){ //验证右边是否满足
dp[i]=(dp[i]+dp[j])%mod;
}
}
}
return dp[s.length()];
}
//10 0000 0000
public boolean valid(String s,int j,int i,int k){
long value=Long.valueOf(s.substring(j,i));
return value<=k && value>=1;
}
我开始以为时间复杂度是O(N^2)会 T 掉,后来写出来才发现其实时间复杂度其实是O(10N) ,并不难,还是题目写少了啊!!!
解法二
一点小优化
public int numberOfArrays(String s, int k) {
int mod=1_000_000_000 + 7;
int[] dp=new int[s.length()+1];
dp[0]=1;
for (int i=1;i<=s.length();i++) {
for (int j=i-1;j>=0 && i-j<=9;j--) {
if(s.charAt(j)=='0') continue;
long value=Long.valueOf(s.substring(j,i));
if(value>k) break; //这一步其实是对上面解法的优化
dp[i]=(dp[i]+dp[j])%mod;
}
}
return dp[s.length()];
}
300. 最长上升子序列
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入:[10,9,2,5,3,7,101,18]
输出:4
解释:最长的上升子序列是 [2,3,7,101],它的长度是 4。
说明:
- 可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
- 你算法的时间复杂度应该为 O(n2) 。
- 进阶:你能将算法的时间复杂度降低到 O(n log n) 吗?
解法一
LIS,这题好像在很多地方见到过了,还是要好好理解下,dp[i] 表示以当前元素结尾的最长上升子序列的长度
public static int lengthOfLIS(int[] nums) {
if (nums==null||nums.length<=0) {
return 0;
}
int[] dp=new int[nums.length];
//Arrays.fill(dp,1);
dp[0]=1;
for (int i=1;i<nums.length;i++) {
dp[i]=1; //初始化 dp[i]=1
for (int j=0;j<i;j++) {
if(nums[i]>nums[j]){
//遍历 i 之前的元素,找一个最大的 dp[j]+1
dp[i]=Math.max(dp[j]+1,dp[i]);
}
}
}
int res=-1;
for (int i=0;i<dp.length;i++) {
res=res>dp[i]?res:dp[i];
}
return res;
}
一开始题目就没看清楚就开始做,以为是连续的,心想这不是 O(N) 的么,为啥要我写 O(N^2) 的🤣

灵魂画手,其实也是一道很简单的 DP(然而我还是没想出来),但是时间复杂度比较高 O(N^2),可以优化成 O(NlogN)
解法二
贪心+二分 这个贪心还是有点骚的,核心思想:
如果前面的数越小,后面接上一个随机数,就会有更大的可能性构成一个更长的“上升子序列”。
定义tail数组,tail[i]中存储长度为 i + 1 的最长递增子序列的最后一个元素,所以我们要做的就是维护 tail 数组,使得各个长度的tail[i]的尽可能地小,这样后面能接的长度就越长,很明显 tail 是个单调递增的数组(反证)所以我们可以在遍历 nums 的时候在 tail 数组中二分寻找第一个大于 nums[i] 的元素,用 nums[i] 替换该位置的元素,这样就使得tail[i]是当前 nums[i] 之前,长度为 i+1 的递增序列最小的结尾元素,当我们遍历完所有的元素,tail 数组的长度就是我们要求的最长递增子序列长度(注意 tail 不一定是合法的最长递增子序列,如果要求出子序列可以在长度增加的时候拷贝一份长度为i-1的数组,然后再操作)
2020.3.20
public static int lengthOfLIS(int[] nums) {
int[] top = new int[nums.length];
int len = 0;
for (int num : nums) {
//寻找左侧最小的堆顶
int index=binarySearch(top,len,num);
if (index == len) {
len++;
}
top[index] = num;
}
return len;
}
//可以搜索
private static int binarySearch(int[] nums, int len, int target) {
int left=0,right=len;
while(left<right){
int mid=left+(right-left)/2;
if(nums[mid]<target){
left=mid+1;
}else {
right=mid;
}
}
return left;
}
首先是记住了这个套路,然后优化了二分的写法

(copy 自从 liweiwei 大佬 题解)
673. 最长递增子序列的个数
给定一个未排序的整数数组,找到最长递增子序列的个数。
示例 1:
输入:[1,3,5,4,7]
输出:2
解释:有两个最长递增子序列,分别是 [1, 3, 4, 7] 和 [1, 3, 5, 7]。
示例 2:
输入:[2,2,2,2,2]
输出:5
解释:最长递增子序列的长度是 1,并且存在 5 个子序列的长度为 1,因此输出 5。
注意: 给定的数组长度不超过 2000 并且结果一定是 32 位有符号整数。
解法一
一开始还没想到,属实菜鸡
public int findNumberOfLIS(int[] nums) {
int n=nums.length;
//dp[i][0] 结尾的最长递增子序列,dp[i][1] 代表个数
int[][] dp=new int[n][2];
int max=0;
for(int i=0;i<n;i++){
dp[i][1]=1;
for(int j=0;j<i;j++){
if(nums[i]>nums[j]){
if(dp[j][0]+1==dp[i][0]){
dp[i][1]+=dp[j][1];
}else if(dp[j][0]+1>dp[i][0]){
dp[i][1]=dp[j][1];
dp[i][0]=dp[j][0]+1;
}
}
}
max=Math.max(max,dp[i][0]);
}
int res=0;
for(int i=0;i<nums.length;i++) {
res+=dp[i][0]==max?dp[i][1]:0;
}
return res;
}
1016. 使序列递增的最小交换次数(LintCode)
有两个具有相同非零长度的整数序列 A 和 B。可以交换它们的一些元素 A[i] 和 B[i]。 注意,两个可交换的元素在它们各自的序列中处于相同的索引位置。进行一些交换之后,A 和 B 需要严格递增。 (当且仅当 A[0] < A[1] < A[2] < … < A[A.length - 1] 时,序列严格递增。)
给定 A 和 B,返回使两个序列严格递增的最小交换次数。 保证给定的输入经过交换可以满足递增的条件。
注意
- A, B 是长度相同的数组,它们的长度范围为 [1, 1000]。
- A[i], B[i] 是在 [0, 2000] 范围内的整数。
样例 1
输入:A = [1,3,5,4], B = [1,2,3,7]
输出:1
解释:交换 A[3] and B[3]. 两个序列变为:
A = [1,3,5,7] 和 B = [1,2,3,4],
此时它们都是严格递增的。
样例 2:
输入:A = [2,4,5,7,10], B = [1,3,4,5,9]
输出:0
解法一
直接抄答案,很巧妙的双序列型 dp,不看答案真想不出来
public int minSwap(int[] A, int[] B) {
if (A == null || B == null || A.length <=0 || B.length <= 0){
return 0;
}
// Write your code here
int n = A.length;
int INF = 0x3f3f3f3f;
//dp[i][0]: A 和 B 前 i 个字符都保持有序,并且不交换第 i 个元素的最小交换次数
//dp[i][1]: A 和 B 前 i 个字符都保持有序,并且交换第 i 个元素的最小交换次数
int[][] dp = new int[n][2];
for(int i = 0; i < n; i++){
Arrays.fill(dp[i], INF);
}
dp[0][0] = 0; dp[0][1] = 1;
for(int i = 1; i < n; i++){
//很巧妙的分类讨论
if(A[i] > A[i-1] && B[i] > B[i-1]){
//前后都不交换
dp[i][0] = dp[i-1][0];
//前后都交换
dp[i][1] = dp[i-1][1]+1;
}
if(A[i] > B[i-1] && B[i] > A[i-1]){
//当前不交换,交换前面的
dp[i][0] = Math.min(dp[i][0], dp[i-1][1]);
//当前交换,前面不交换
dp[i][1] = Math.min(dp[i][1], dp[i-1][0]+1);
}
}
int res = Math.min(dp[n-1][0],dp[n-1][1]);
return res == INF ? 0 : res;
}
354. 俄罗斯套娃信封问题
给定一些标记了宽度和高度的信封,宽度和高度以整数对形式 (w, h) 出现。当另一个信封的宽度和高度都比这个信封大的时候,这个信封就可以放进另一个信封里,如同俄罗斯套娃一样。
请计算最多能有多少个信封能组成一组“俄罗斯套娃”信封(即可以把一个信封放到另一个信封里面)。
说明: 不允许旋转信封。
示例:
输入:envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出:3
解释:最多信封的个数为 3, 组合为:[2,3] => [5,4] => [6,7]。
解法一
public int maxEnvelopes(int[][] envelopes) {
int [] dp=new int[envelopes.length];
//lamdba 会比较慢
Arrays.sort(envelopes,(a,b)->(a[0]-b[0])); //保证后面的不会被前面的装进去就行了
int res=0;
for (int i=0;i<envelopes.length;i++) {
dp[i]=1;
for (int j=0;j<i;j++) {
if (envelopes[i][0]>envelopes[j][0] && envelopes[i][1]>envelopes[j][1]){
dp[i]=Math.max(dp[j]+1,dp[i]);
}
}
res=Math.max(res,dp[i]);
}
return res;
}
其实和上面的 LIS 是一样的,所以我放在了一起,差点 bugfree,被空输入坑了一发,可惜这个解法并不是最优解,而且也不符合这题的困难 tag,这题的最优解应该是利用上面的贪心+二分的做法,这里实在是能力时间都有限,没法去研究那种解法,暂且先用这个解法吧
解法二
2020.3.20 阿里笔试考了这一题,dp 超时了。
public int maxEnvelopes(int[][] envelopes) {
Arrays.sort(envelopes,(a,b)->a[0]!=b[0]?a[0]-b[0]:b[1]-a[1]); //这个排序很关键
int N=envelopes.length;
int[] top=new int[N];
int len=0;
for(int i=0;i<N;i++){
int cur=envelopes[i][1];
//二分搜索堆顶,找第一个小于当前牌的
int index=binarySearch(top,cur,len);
if(index==len){ //没找到合适的位置
len++; //新建牌堆,牌堆++
}
top[index]=cur;
}
return len;
}
public int binarySearch(int[] top,int target,int len){
int left=0,right=len;
while(left<right){
int mid=left+(right-left)/2;
if(top[mid]<target){
left=mid+1;
}else{
right=mid;
}
}
return left;
}
第一步的排序很关键,如果只按照宽度排好序之后,对高度求一次最长递增子序列就是我们的答案,但是有一个问题就是题目说了:宽度和高度都比当前信封大的时候才能装进去,如果有两个信封是(1,3) (1,5)那么前者是不能被后者装进去的,所以我们需要在这里做一下处理,在宽度相同的时候,让高度降序排列,这样在对高度求最递增子序列的时候就不会出现错误了
UPDATE: 2020.7.13
func maxEnvelopes(env [][]int) int {
sort.Slice(env, func(i int, j int) bool {
if env[i][0] == env[j][0]{
return env[i][1] > env[j][1]
}
return env[i][0] < env[j][0]
})
var tail = make([]int, len(env))
var tlen = 0
for i := 0; i < len(env); i++{
idx := search(tail, env[i][1], tlen)
if idx == tlen{
tlen++
}
tail[idx] = env[i][1]
}
return tlen
}
func search(nums []int, target int, tlen int) int {
var left = 0
var right = tlen-1
var res = tlen
for left <= right{
mid := left+(right-left)/2
if nums[mid] >= target{
res = mid
right = mid - 1
}else{
left = mid + 1
}
}
return res
}
53. 最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入:[-2,1,-3,4,-1,2,1,-5,4],
输出:6
解释:连续子数组 [4,-1,2,1] 的和最大,为 6。
进阶:
如果你已经实现复杂度为 O(n) 的解法,尝试使用更为精妙的分治法求解。
解法一
动态规划递推的解法,没啥好说的,这题其实还有一道姊妹题,要求出最大子序列,不仅仅是最大值,我放到了滑动窗口专题中
//这次是直接在 Web 上写的
public int maxSubArray(int[] nums) {
if(nums==null || nums.length==0){
return 0;
}
int[] dp=new int[nums.length];
//一开始没处理好 Wa 了一发
int max=dp[0]=nums[0];
for(int i=1;i<nums.length;i++){
if(dp[i-1]<=0){
dp[i]=nums[i];
}else{
dp[i]=dp[i-1]+nums[i];
}
max=Math.max(max,dp[i]);
}
return max;
}
解法二
根据二维改一维
public int maxSubArray(int[] nums) {
if(nums==null || nums.length==0){
return 0;
}
int dp1=nums[0],dp2=0,max=nums[0];
for (int i=1;i<nums.length;i++) {
if (dp1<=0) {
dp2=nums[i];
}else{
dp2=dp1+nums[i];
}
dp1=dp2;
max=Math.max(max,dp2);
}
return max;
}
感觉一维的不用去理解含义,能根据二维改出来就 ok 了,重点是理解多维的
646. 最长数对链
给出 n 个数对。 在每一个数对中,第一个数字总是比第二个数字小。
现在,我们定义一种跟随关系,当且仅当 b < c 时,数对(c, d) 才可以跟在 (a, b) 后面。我们用这种形式来构造一个数对链。
给定一个对数集合,找出能够形成的最长数对链的长度。你不需要用到所有的数对,你可以以任何顺序选择其中的一些数对来构造。
示例 :
输入:[[1,2], [2,3], [3,4]]
输出:2
解释:最长的数对链是 [1,2] -> [3,4]
注意:
- 给出数对的个数在 [1, 1000] 范围内。
解法一
动态规划
public int findLongestChain(int[][] pairs) {
Arrays.sort(pairs,(a,b)->a[0]-b[0]);
int[] dp=new int[pairs.length];
int res=0;
for (int i=0;i<pairs.length;i++) {
dp[i]=1;
for (int j=0;j<i;j++) {
if (pairs[i][0]>pairs[j][1]) {
dp[i]=Math.max(dp[i],dp[j]+1);
}
}
res=res>dp[i]?res:dp[i];
}
return res;
}
注意这里没有要求顺序,所以先给他排个序,然后再进行 DP,如果不排序很难 dp,dp[i] 表示当前数对能构成的最长链,dp 过程和上面的最长上升子序列相同
解法二
贪心,也是最优解,同样先排序,不过是按照第二个元素来排序,核心思想
每次都在列表中找第二个元素最小的数对依次组成链,最后得到的一定是最长的链
public int findLongestChain(int[][] pairs) {
Arrays.sort(pairs,(a,b)->a[1]-b[1]);
int res=1;
int tail=pairs[0][1];
for (int i=1;i<pairs.length;i++) {
if (pairs[i][0]>tail) {
res++;
tail=pairs[i][1];
}
}
return res;
}
解法三
也就是上面说的分治法,分治法在这里并不是最优解,时间复杂度O(NlogN),但是思路还是很巧妙,首先也是讲数组一分为二,然后最大序列和就有三种情况
- 全在左边
- 全在右边
- 跨中点,两边都有
然后统计三个值得最大值,递归子过程求解,代码就不写了,后面想起来有时间再补
376. 摆动序列
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反,[1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
示例 1:
输入:[1,7,4,9,2,5]
输出:6
解释:整个序列均为摆动序列。
示例 2:
输入:[1,17,5,10,13,15,10,5,16,8]
输出:7
解释:这个序列包含几个长度为 7 摆动序列,其中一个可为 [1,17,10,13,10,16,8]。
示例 3:
输入:[1,2,3,4,5,6,7,8,9]
输出:2
进阶:
- 你能否用 O(n) 时间复杂度完成此题?
解法一
O(N^2 ) 动态规划,dp[i] 代表目前为止以 nums[i] 结尾的最长的上升摇摆序列,down[i] 代表目前为止以 nums[i] 结尾的最长的下降摇摆序列,后面过程就和上面的LIS的解法类似了
public int wiggleMaxLength(int[] nums) {
if (nums==null || nums.length<=0) {
return 0;
}
int []up=new int[nums.length];
int []down=new int[nums.length];
for (int i=0;i<nums.length;i++) {
up[i]=1; down[i]=1; //初始化
for (int j=0;j<i;j++) {
if(nums[i]>nums[j]){
//找一个最大的下降沿
up[i]=Math.max(up[i],down[j]+1);
}else if(nums[i]<nums[j]){
//找一个最大的上升沿
down[i]=Math.max(down[i],up[j]+1);
}
}
}
return Math.max(up[nums.length-1],down[nums.length-1]);
}
解法二
线性动态规划,其实上面的循环找最大操作有点多余,如果nums[i]>nums[i-1] 那么以 nums[i] 为上升沿结尾(摆动上升)的最长摇摆序列 up[i]=down[i-1]+1
public int wiggleMaxLength2(int[] nums) {
if (nums==null || nums.length<=0) {
return 0;
}
int []up=new int[nums.length];
int []down=new int[nums.length];
up[0]=down[0]=1;
for (int i=1;i<nums.length;i++) {
if(nums[i]>nums[i-1]){
up[i]=down[i-1]+1;
down[i]=down[i-1];
}else if(nums[i]<nums[i-1]){
down[i]=up[i-1]+1;
up[i]=up[i-1];
}else{
//相等的时候别忘了继承前面的状态
down[i]=down[i-1];
up[i]=up[i-1];
}
}
return Math.max(up[nums.length-1],down[nums.length-1]);
}
我感觉能写出 O(1) 的前提是先写出 O(N) 的,写出 O(N) 的之后再改成 O(1) 会比较简单
public int wiggleMaxLength(int[] nums) {
if (nums==null || nums.length<=0) {
return 0;
}
int up=1;
int down=1;
for (int i=1;i<nums.length;i++) {
if (nums[i]>nums[i-1]) {
up=down+1;
}else if (nums[i]>nums[i-1]){
down=up+1;
}//else 就是不变
}
return Math.max(up,down);
}
978. 最长湍流子数组
当 A 的子数组 A[i], A[i+1], ..., A[j] 满足下列条件时,我们称其为湍流子数组:
- 若
i <= k < j,当k为奇数时,A[k] > A[k+1],且当k为偶数时,A[k] < A[k+1]; - 或 若
i <= k < j,当k为偶数时,A[k] > A[k+1],且当k为奇数时,A[k] < A[k+1]。
也就是说,如果比较符号在子数组中的每个相邻元素对之间翻转,则该子数组是湍流子数组。(上面的是废话)
返回 A 的最大湍流子数组的长度。
示例 1:
输入:[9,4,2,10,7,8,8,1,9]
输出:5
解释:(A[1] > A[2] < A[3] > A[4] < A[5])
示例 2:
输入:[4,8,12,16]
输出:2
示例 3:
输入:[100]
输出:1
提示:
1 <= A.length <= 400000 <= A[i] <= 10^9
解法一
在滑窗 tag 里发现的,一直没往 dp 上想,看了评论区才发现😂,这题其实是上面 376. 摆动序列的弱化,这里是要求连续的,但是做法还是一样的
//动态规划,从滑窗 tag 过来的。.. 没往 dp 上想,看了评论区才想起来
public int maxTurbulenceSize(int[] A) {
if(A==null || A.length<=0){
return 0;
}
int up=1,down=1;
int res=1;
for (int i=1;i<A.length;i++) {
if(A[i]>A[i-1]){
up=down+1;
down=1;
}else if (A[i]<A[i-1]){
down=up+1;
up=1;
}else{
up=1;down=1;
}
res=Math.max(res,Math.max(up,down));
}
return res;
}
解法二
滑窗,也是一开始的做法,比较简单
//优化 if 条件
public int maxTurbulenceSize(int[] A) {
if(A==null || A.length<=0){
return 0;
}
int left=0;
int res=1;
for(int right=left+1;right<A.length;right++){
if(A[right]==A[right-1]){ //跳过相等的
left=right;
continue;
}
//优化了 if 条件,之前看别人题解学到的
if(right>=2 && (A[right]>A[right-1])==(A[right-1]>A[right-2])){
left=right-1; //left 跳到中间值
}
res=Math.max(res,right-left+1);
}
return res;
}
96. 不同的二叉搜索树
Given n, how many structurally unique BST’s (binary search trees) that store values 1 … n?
Example:
Input: 3
Output: 5
Explanation:
Given n = 3, there are a total of 5 unique BST's:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
解法一
这个解法实际上来自 95. 不同的二叉搜索树 II
public static int numTrees(int n) {
return generateTree(1,n).size();
}
public static List<TreeNode> generateTree(int start,int end){
List<TreeNode> res=new ArrayList<>();
if (start>end) {
res.add(null);
return res;
}
for (int i=start;i<=end;i++) {
List<TreeNode> left=generateTree(start,i-1);
List<TreeNode> right=generateTree(i+1,end);
for (TreeNode l:left) {
for (TreeNode r:right) {
TreeNode currentNode=new TreeNode(i);
currentNode.left=l;
currentNode.right=r;
res.add(currentNode);
}
}
}
return res;
}
这种写法很明显过不了这题,时间复杂度太高了,但是这个方法可以求出所有的 BST 集合。
解法二
动态规划,dp[i]代表长度为 i 的递增序列构成的不同的 BST 的数量(序列从1 到 i 递增)
递推公式:dp[i]=dp[i-1]* dp[n-i]
public int numTrees(int n) {
if (n<=1) {
return 1;
}
int []dp=new int[n+1];
dp[0]=1;
dp[1]=1;
for (int i=2;i<=n;i++) { //控制序列长度 直到我们求得 n
for (int j=1;j<=i;j++) { //控制根的选择
//累加和,j 为根节点 dp[j-1] 代表左子树数量,dp[i-j] 代表右子树数量
dp[i]+=dp[j-1]*dp[i-j];
}
}
return dp[n];
}
以 i 位置元素为根节点,可以得出可能的 BST 数量为,[1 ~ i-1] 可以构成的 BST 数量 乘以 [i+1,n]可以构成的 BST 数量,也就是_左子树 * 右子树_ ,再推广到整个序列的 BST 总数,其实也就是 以每个元素为根节点构成的 BST 的数量之和 ,需要理解的地方就是dp[i] 的含义,明确本题中dp[i] 其实只和长度 i有关而和内容无关,比如 1,2,3 和 4,5,6 所能构成的 BST 数量其实是相同的
解法三
卡塔兰数,递推式 Gn+1 =2(2n+1)/ n+2 * Gn
public int numTrees3(int n) {
long C = 1;
for(int i = 0; i < n; ++i){
C = C * 2 * (2 * i + 1) /(i + 2);
}
return (int) C;
}
120. 三角形最小路径和
给定一个三角形,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
例如,给定三角形:
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
说明:
如果你可以只使用 O(n) 的额外空间(n 为三角形的总行数)来解决这个问题,那么你的算法会很加分
解法一
二维 dp,emmm,一开始写成贪心了。贪心明显是错的
//dp 做法 O(N^2) 空间
public int minimumTotal(List<List<Integer>> triangle) {
int rows=triangle.size();
//dp[i][j] 代表的是每 i 层第 j 个元素到最底层的最短距离
int[][] dp=new int[rows+1][rows+1]; //row+1
/*for (int i=0;i<triangle.get(rows-1).size();i++) {
//给最后一行赋初始值
dp[rows-1][i]=triangle.get(rows-1).get(i);
}
for (int i=rows-2;i>=0;i--) {
for (int j=0;j<triangle.get(i).size();j++) {
//核心递推式 dp[i][j]=min(dp[i+1][j],dp[i+1][j+1])+triangle(i)(j)
dp[i][j]=Math.min(dp[i+1][j],dp[i+1][j+1])+triangle.get(i).get(j);
}
}*/
//直接从最后一行开始,这样就不用手动给最后一行赋初始值了
for (int i=rows-1;i>=0;i--) {
for (int j=0;j<triangle.get(i).size();j++) {
//核心递推式 dp[i][j]=min(dp[i+1][j],dp[i+1][j+1])+triangle(i)(j)
dp[i][j]=Math.min(dp[i+1][j],dp[i+1][j+1])+triangle.get(i).get(j);
}
}
return dp[0][0];
}
解法二
记忆化递归,也很快
//记忆化递归
public int minimumTotal2(List<List<Integer>> triangle) {
//用 Integer 比较好,方便判空
Integer [][] cache=new Integer[triangle.size()][triangle.size()];
return minimumTotal(triangle,0,0,cache);
}
public int minimumTotal(List<List<Integer>> triangle,int cen,int index,Integer[][]cache) {
if (cache[cen][index]!=null) {
return cache[cen][index];
}
if (cen==triangle.size()-1) {
return triangle.get(cen).get(index);
}
int left=minimumTotal(triangle,cen+1,index,cache);
int right=minimumTotal(triangle,cen+1,index+1,cache);
return cache[cen][index]=triangle.get(cen).get(index)+(left<right?left:right);
}
解法三
//dp O(N) 空间
public int minimumTotal(List<List<Integer>> triangle) {
int rows=triangle.size();
//dp[i] 代表的是每一层第 i 个元素到最底层的最短距离
//上面二维 dp 实际上也只和下一层的状态有关,所以我们可以重复的使用这个数组保存每一层的状态
int[] dp=new int[rows+1];
for (int i=rows-1;i>=0;i--) {
for (int j=0;j<triangle.get(i).size();j++) {
//到这里其实 Math.min() 里面的都是上一次循环的结果
//也就是下一层的,对应当前 j 位置左右两个相邻节点的最小距离
dp[j]=Math.min(dp[j+1],dp[j])+triangle.get(i).get(j);
}
}
return dp[0];
}
O(N) 空间复杂度,只和下面那一层的每一个元素的 dp[i] 有关,所以可以直接改成一维 dp
UPDATE: 2020.7.14
今天的打卡题,写了一个从上而下的 dp,需要处理边界会麻烦一点,和之前的反着的,果然刷题主要还是刷一个感觉,想记住题目解法是不可能的,能锻炼一些思考的能力才是关键
func minimumTotal(triangle [][]int) int {
if len(triangle) <= 0{
return 0
}
var INF = 1<<31
var n = len(triangle)
var dp = make([]int, n)
for i := 0; i < n; i++{
dp[i] = INF
}
dp[0] = triangle[0][0]
var res = INF
for i := 1; i < n; i++{
for j :=i; j >=0; j--{
if j == 0{
dp[j] = dp[j] + triangle[i][j]
}else if j == i{
dp[j] = dp[j-1] + triangle[i][j]
}else{
dp[j] = Min(dp[j], dp[j-1]) + triangle[i][j]
}
if i == n-1{
res = Min(res, dp[j])
}
}
}
if res == INF{
return triangle[0][0]
}
return res
}
func Min(a, b int) int {
if a < b{
return a
}
return b
}
121. 买卖股票的最佳时机
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易(即买入和卖出一支股票),设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
示例 1:
输入:[7,1,5,3,6,4]
输出:5
解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 ,注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
示例 2:
输入:[7,6,4,3,1]
输出:0
解释:在这种情况下,没有交易完成,所以最大利润为 0。
解法一
非动态规划的思路,还是挺简单的,求个最大的差值就 ok,因为只能买一次
//非递归的思路
public int maxProfit(int[] prices) {
if (prices==null || prices.length<=0) {
return 0;
}
int min=Integer.MAX_VALUE,max=0;
for (int i=0;i<prices.length;i++) {
//当天价格减去 *之前* 价格最低的买入时机
max=Math.max(max,prices[i]-min);
//统计价格最低的买入时机
min=Math.min(min,prices[i]);
}
return max;
}
解法二
既然是动态规划的题,自然得写个动态规划的版本
public int maxProfit(int[] prices) {
if (prices==null || prices.length<=0) {
return 0;
}
int[][] dp=new int[prices.length][2];
dp[0][0]=0;
dp[0][1]= -prices[0];
for (int i=1;i<prices.length;i++) {
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+[i]);
dp[i][1]=Math.max(dp[i-1][1],-prices[i]);
}
return dp[prices.length-1][0];
}
其实改成一维的就和上面的一模一样了
122. 买卖股票的最佳时机 II
给定一个数组,它的第 i 个元素是一支给定股票第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易(多次买卖一支股票)。
**注意:**你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:[7,1,5,3,6,4]
输出:7
解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出,这笔交易所能获得利润 = 5-1 = 4 。
随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,这笔交易所能获得利润 = 6-3 = 3 。
示例 2:
输入:[1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出,这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入:[7,6,4,3,1]
输出:0
解释:在这种情况下,没有交易完成,所以最大利润为 0。
解法一
正常的思路(非动态规划),注意审题,上面的只能买一次,这里是不限制次数的
public int maxProfit(int[] prices) {
if (prices==null || prices.length<=0) {
return 0;
}
int ans=0;
for (int i=1;i<prices.length;i++) {
if (prices[i]>prices[i-1]) {
ans+=prices[i]-prices[i-1];
}
}
return ans;
}
这里的代码还是很有迷惑性的,实际上分了三种情况,有两种合并了
单独交易日:明天比今天价格高,今天买,明天卖
连续上涨交易日:开始的第一天买 , 涨停的最后一天卖最有利,或者也可以转换成说
除了第一天,每天都卖了又买,也就是pn-p1 = (p2-p1)+(p3-p2)+....(pn-pn-1)很自然的就转换成了单独交易日的情况 连续下降交易日:不买卖最有利
如果还是不明白可以看看官方的图

A->D 是一段连续上涨日,D-A 的差值 就是 A->D 各个相邻节点差值之和
解法二
我们的主角,动态规划
//dp 的思路
public int maxProfit(int[] prices) {
if (prices==null || prices.length<=0) {
return 0;
}
int[][] dp=new int[prices.length][2];
dp[0][0]=0;
dp[0][1]=-prices[0];
for (int i=1;i<prices.length;i++) {
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);
}
return dp[prices.length-1][0];
}
第一眼看可能觉得看不懂,熟悉了就知道了,其实都是套路,股票题特有的套路,先考虑题目有几种状态,这题说了不限制次数,那么就不考虑次数的问题,然后剩下的状态就是:那一天,和是否持有股票,所以我们用一个二维的数组来表述这两种状态 比如dp[i][0] 则代表第 i 天不持有股票的最大收益,dp[i][1]则代表第 i 天持有股票的最大收益,然后我们再看看状态转换的过程

其实无非就是这两个状态之间的转换,然后根据这个状态转换的过程就可以很轻易的写出我们的状态转换方程
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i]);
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);
不过这里其实也很容易就可以改成一唯的 dp,空间复杂度变为 O(1),因为当天的最大收益只和前一天的最大收益相关,两个变量就是足够表示
public int maxProfit(int[] prices) {
if (prices==null || prices.length<=0) {
return 0;
}
int hlod=-prices[0];
int empty=0;
for (int i=1;i<prices.length;i++) {
//保存前一天的状态
int temp=empty;
empty=Math.max(empty,hlod+prices[i]);
hlod=Math.max(hlod,temp-prices[i]);
}
return empty;
}
这里我感觉 leetcode 的 case 有问题,我开始没有缓存前一天的 empty 值,直接将 empty 带到 hold 去了,结果还过了。不过我懒得去想 case 了,反正提交了 leecode 也不会理我😅
123. 买卖股票的最佳时机 III
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意: 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:[3,3,5,0,0,3,1,4]
输出:6
解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。
随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 2:
输入:[1,2,3,4,5]
输出:4
解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出,这笔交易所能获得利润 = 5-1 = 4 。
注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。
因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入:[7,6,4,3,1]
输出:0
解释:在这个情况下,没有交易完成,所以最大利润为 0
解法一
二维动态规划,定义出每个状态,然后转换就可以了
public int maxProfit(int[] prices){
if (prices==null || prices.length<=0) {
return 0;
}
//状态定义:
//j=0 什么都不做
//j=1 第一次买入
//j=2 第一次卖出
//j=3 第二次买入
//j=4 第二次卖出
int[][] dp=new int[prices.length][5];
//这样会溢出
//Arrays.fill(dp[0],Integer.MIN_VALUE);
//这样可以过,但是感觉还是判断一下好
//Arrays.fill(dp[0],-0x3f3f3f3f);
int INF=Integer.MIN_VALUE,n=prices.length;
Arrays.fill(dp[0],INF); //不可达状态
dp[0][0]=0;
dp[0][1]=-prices[0];
for(int i=1;i<n;i++){
dp[i][0]=0;
dp[i][1]=Math.max(-prices[i],dp[i-1][1]);
dp[i][2]=Math.max(dp[i-1][1]+prices[i],dp[i-1][2]);
dp[i][3]=Math.max(dp[i-1][2]!=INF?dp[i-1][2]-prices[i]:INF,dp[i-1][3]);
dp[i][4]=Math.max(dp[i-1][3]!=INF?dp[i-1][3]+prices[i]:INF,dp[i-1][4]);
}
return Math.max(Math.max(dp[n-1][0],dp[n-1][2]),dp[n-1][4]);
}
因为题目的数据不是特别大,没有超过
10^9直接初始化为-0x3f3f3f3f就不用判断前面的状态是否可达了,
解法二
优化成一维的
public int maxProfit(int[] prices){
if (prices==null || prices.length<=0) {
return 0;
}
int[] dp=new int[5];
int n=prices.length;
Arrays.fill(dp,-0x3f3f3f3f);
dp[0]=0;
dp[1]=-prices[0];
for(int i=1;i<n;i++){
//逆序递推避免覆盖(其实正着写也是对的,这题相邻的状态不会同时更新,但是为了规范最好还是逆序写)
dp[4]=Math.max(dp[3]+prices[i],dp[4]);
dp[3]=Math.max(dp[2]-prices[i],dp[3]);
dp[2]=Math.max(dp[1]+prices[i],dp[2]);
dp[1]=Math.max(-prices[i],dp[1]);
dp[0]=0;
}
return Math.max(Math.max(dp[0],dp[2]),dp[4]);
}
188. 买卖股票的最佳时机 IV
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:[2,4,1], k = 2
输出:2
解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入:[3,2,6,5,0,3], k = 2
输出:7
解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出,这笔交易所能获得利润 = 6-2 = 4 。
随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。
解法一
这题其实就是求上面一题的通解,上面的代码规律已经非常明显了,j为奇数的时候买入,偶数的时候卖出,我们统计最后偶数的最大值就可以
public int maxProfit(int k, int[] prices) {
if (prices==null || prices.length<=0 || k<=0) {
return 0;
}
if(k>prices.length/2){
return maxProfit(prices);
}
//k 次交易,2*k+1 种状态
int[] dp=new int[2*k+1];
int n=prices.length;
int res=0;
Arrays.fill(dp,-0x3f3f3f3f);
dp[0]=0;
dp[1]=-prices[0];
for(int i=1;i<n;i++){
//注意倒推
for(int j=2*k;j>0;j--){
if((j&1)==1){
dp[j]=Math.max(dp[j-1]-prices[i],dp[j]);
}else{
dp[j]=Math.max(dp[j-1]+prices[i],dp[j]);
res=Math.max(dp[j],res);
}
}
}
return res;
}
public int maxProfit(int[] prices) {
if (prices==null || prices.length<=0) {
return 0;
}
int ans=0;
for (int i=1;i<prices.length;i++) {
if (prices[i]>prices[i-1]) {
ans+=prices[i]-prices[i-1];
}
}
return ans;
}
解法二
正常的 DP 通解
//常规 2 维解法
public int maxProfit(int k, int[] prices) {
if (prices==null || prices.length<=0 || k<=0) {
return 0;
}
if(k>prices.length/2){
return maxProfit(prices);
}
//第 k 次交易,持股/不持股
int[][] dp=new int[k+1][2];
int n=prices.length;
int res=0;
int INF=-0x3f3f3f3f;
for(int i=0;i<=k;i++){
Arrays.fill(dp[i],INF);
}
//其实这题难搞的就是对于初始状态的 init
//第一天没有交易和第一天有一次交易的初始值
dp[0][0]=0;dp[0][1]=INF;
dp[1][0]=0;dp[1][1]=-prices[0];
for(int i=1;i<n;i++){
//注意倒推
for(int j=k;j>0;j--){
//这里将买入和卖出作为一个状态,所以这里买入新股票,肯定就是属于下一次交易了
//所以这里的 j 需要减一,代表上一次交易卖出时候的收益
dp[j][0]=Math.max(dp[j][1]+prices[i],dp[j][0]);
dp[j][1]=Math.max(dp[j-1][0]-prices[i],dp[j][1]);
res=Math.max(dp[j][0],res);
}
}
return res;
}
public int maxProfit(int[] prices) {
if (prices==null || prices.length<=0) {
return 0;
}
int ans=0;
for (int i=1;i<prices.length;i++) {
if (prices[i]>prices[i-1]) {
ans+=prices[i]-prices[i-1];
}
}
return ans;
}
714. 买卖股票的最佳时机含手续费
给定一个整数数组 prices,其中第 i 个元素代表了第 i 天的股票价格 ,非负整数 fee 代表了交易股票的手续费用
你可以无限次地完成交易,但是你每次交易都需要付手续费。如果你已经购买了一个股票,在卖出它之前你就不能再继续购买股票了。
返回获得利润的最大值。
示例 1:
输入:prices = [1, 3, 2, 8, 4, 9], fee = 2
输出:8
解释:能够达到的最大利润:
在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润:((8 - 1) - 2) + ((9 - 4) - 2) = 8.
注意:
0 < prices.length <= 50000.0 < prices[i] < 50000.0 <= fee < 50000.
解法一
我起了,一枪秒了,有什么好说的?
public int maxProfit(int[] prices, int fee) {
if (prices==null || prices.length<=0) {
return 0;
}
int[][] dp=new int[prices.length][2];
dp[0][0]=0;
dp[0][1]=-prices[0];
for (int i=1;i<prices.length;i++) {
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+prices[i]-fee);
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);
}
return dp[prices.length-1][0];
}
改为 O(1) 空间
//改为 O(1)
public int maxProfit(int[] prices, int fee) {
if (prices==null || prices.length<=0) {
return 0;
}
int empty=0;
int hold=-prices[0];
for (int i=1;i<prices.length;i++) {
int temp=empty;
empty=Math.max(empty,hold+prices[i]-fee);
hold=Math.max(hold,temp-prices[i]);
}
return empty;
}
309. 最佳买卖股票时机含冷冻期
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
- 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)
- 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)
示例:
输入:[1,2,3,0,2]
输出:3
解释:对应的交易状态为:[买入,卖出,冷冻期,买入,卖出]
解法一
依然是上面题的升级版,相比上一题又多了个限制条件,加了 cd,买卖一次后有一天的 cd,当天不能再买
public int maxProfit(int[] prices) {
if (prices==null || prices.length<=0) {
return 0;
}
//dp[i][0] 代表第 i 天不持有股票的最大利润
//dp[i][1] 代表第 i 天持有股票的最大利润
int[][] dp=new int[prices.length][2];
dp[0][0]=0;
dp[0][1]=-prices[0];
for (int i=1;i<prices.length;i++) {
//这些玩意想起还是蛮打脑阔的
dp[i][0]=Math.max(dp[i-1][1]+prices[i],dp[i-1][0]);
//dp[i][1]=Math.max(i<2?-prices[i]:dp[i-2][0]-prices[i],dp[i-1][1]);
//这里 i<2 就是第一次循环,i=1, 也就是第二天持有股票,所以肯定是首次买股票,直接初始化为 -prices[1]
//昨天有股票,或者昨天冷冻前天卖出
dp[i][1]=Math.max(i<2?-prices[1]:dp[i-2][0]-prices[i],dp[i-1][1]);
}
return dp[prices.length-1][0];
}
评论区很多的解法都是用了三个状态数组,相比这种多了一个 冷冻期的最大值,感觉挺迷惑的。虽然结果是对的,但是总时感觉别扭,所以我们还是按照上面的思路,用两个状态表示,状态转换图和上面是一样的

当天持有股票的最大收益,就是你当天买股票,或者 rest 啥也不干延续前一天的状态,两者的最大值
这里和上面不同的就是从不持有股票 到持有股票(也就是买股票)的情况, 因为有冷冻期的存在,所以你当天买股票的最大值不再是昨天不持有股票的最大值,而是前天不持有股票的最大值
解法三
改为空间复杂度 O(1) 的
public int maxProfit(int[] prices) {
if (prices==null || prices.length<=0) {
return 0;
}
int hold=-prices[0];
int empty=0;
//前一天买出的最大收益
int prePre=0;
for (int i=1;i<prices.length;i++) {
int temp=empty;
empty=Math.max(hold+prices[i],empty);
hold=Math.max(i<2?-prices[1]:prePre-prices[i],hold);
//到这里 pre 就变成了前一天
prePre=temp;
}
return empty;
}
看了下评论区还是蛮多争议的,感觉这里根据 dp[i-2] 转换有点不好理解,然后翻了翻评论区看见了大神的回答
dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])
dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])添加 “冷冻期” 条件后,买入的前一天是不能卖的,而
dp[i-1][0] - prices[i]并不能确保i-1 天不卖出所以进一步拆解
dp[i-1][0], 套用上面的转换方程可以得到
dp[i-1][0] = max(dp[i-2][0], dp[i-2][1] + prices[i-1])再带入原式子,则可以得到
dp[i][1] = max(dp[i-1][1], max(dp[i-2][0], dp[i-2][1] + prices[i-1]) - prices[i])其中
dp[i-2][1] + prices[i-1]代表着“i-1 发生了卖出行为”,有违题意,应予删除,得下式,最终和上面的状态转换方程一致
dp[i][1] = max(dp[i-1][1], max(dp[i-2][0]) - prices[i])这样一证明就很清楚了
1269. 停在原地的方案数
有一个长度为 arrLen 的数组,开始有一个指针在索引 0 处。
每一步操作中,你可以将指针向左或向右移动 1 步,或者停在原地(指针不能被移动到数组范围外)。
给你两个整数 steps 和 arrLen ,请你计算并返回:在恰好执行 steps 次操作以后,指针仍然指向索引 0 处的方案数。
由于答案可能会很大,请返回方案数 模 10^9 + 7 后的结果。
示例 1:
输入:steps = 3, arrLen = 2
输出:4
解释:3 步后,总共有 4 种不同的方法可以停在索引 0 处。
向右,向左,不动
不动,向右,向左
向右,不动,向左
不动,不动,不动
示例 2:
输入:steps = 2, arrLen = 4
输出:2
解释:2 步后,总共有 2 种不同的方法可以停在索引 0 处。
向右,向左
不动,不动
示例 3:
输入:steps = 4, arrLen = 2
输出:8
提示:
1 <= steps <= 5001 <= arrLen <= 10^6
解法一
11.24 的周赛最后一题,很可惜没做出来。要是把这题放在第三题我可能就做出来了。还是菜啊
public int numWays(int steps, int arrLen) {
int mod=1_000_000_007;
long[][] dp=new long[steps+1][steps+1];
dp[0][0]=1; //dp[i][j] 的含义是 i 步之后处于 j 位置的方案数
for (int i=1;i<=steps;i++) {
//i 步能达到的最大距离就是 i, 所以我们这里取一个最小值
int k=Math.min(i,arrLen-1);
for (int j=0;j<=k;j++) {
if (j==0) {
dp[i][j]=(dp[i-1][j+1]+dp[i-1][j])%mod;
}else if (j<k) {
dp[i][j]=(dp[i-1][j-1]+dp[i-1][j+1]+dp[i-1][j])%mod;
}else{ //大于 k 就只能是从右边过来的
dp[i][j]=(dp[i-1][j-1]+dp[i-1][j])%mod;
}
}
}
return (int)dp[steps][0];
}
解法二
我比较喜欢的记忆化递归😁,10ms 甚至比上面还快一点
int mod=1_000_000_007;
//cache
Long[][] cache;
public int numWays(int steps, int arrLen) {
int maxIndex=Math.min(steps,arrLen-1);
cache=new Long[steps+1][maxIndex+1];
return (int)dfs(steps,0,maxIndex);
}
public long dfs(int steps, int index,int maxIndex) {
if (steps==0) {
return index==0?1:0;
}
if (index<0 || index > maxIndex ) {
return 0;
}
if (cache[steps][index]!=null) {
return cache[steps][index];
}
//steps 一直在递减,steps 最多走到 steps 位置
//为了节约时间可以在这里优化下
maxIndex=Math.min(steps,maxIndex);
//不动
long res=dfs(steps-1,index,maxIndex);
//向左
res+=dfs(steps-1,index-1,maxIndex);
//向右
res+=dfs(steps-1,index+1,maxIndex);
return cache[steps][index]=res%mod;
}
152. 乘积最大子序列
给定一个整数数组 nums ,找出一个序列中乘积最大的连续子序列(该序列至少包含一个数)。
示例 1:
输入:[2,3,-2,4]
输出:6
解释:子数组 [2,3] 有最大乘积 6。
示例 2:
输入:[-2,0,-1]
输出:0
解释:结果不能为 2, 因为 [-2,-1] 不是子数组。
解法一
自己最开始自己写出来的脑瘫 dp
public static int maxProduct(int[] nums) {
int[] dp1=new int[nums.length];
int[] dp2=new int[nums.length];
//最大值
dp1[0]=nums[0]>=0?nums[0]:0;
//最小值
dp2[0]=nums[0]>=0?0:nums[0];
int max=nums[0]>0?dp1[0]:dp2[0];
for(int i=1;i<nums.length;i++){
if (nums[i]>0) {
if (nums[i-1]<0) {
dp1[i]=dp1[i-1]!=0?nums[i]*dp1[i-1]:nums[i];
dp2[i]=dp2[i-1]*nums[i];
}else if(nums[i-1]>0){
dp1[i]=dp1[i-1]*nums[i];
dp2[i]=dp2[i-1]!=0?nums[i]*dp2[i-1]:0;
}else{
dp1[i]=nums[i];
dp2[i]=0;
}
}else if (nums[i]<0) {
if (nums[i-1]<0) {
dp1[i]=dp2[i-1]*nums[i];
dp2[i]=dp1[i-1]!=0?dp1[i-1]*nums[i]:nums[i];
}else if(nums[i-1]>0){
dp1[i]=dp1[i-1]!=0?nums[i]*dp2[i-1]:0;
dp2[i]=dp1[i-1]*nums[i];
}else{
dp1[i]=0;
dp2[i]=nums[i];
}
}else{
dp1[i]=0;
dp2[i]=0;
}
//System.out.println(dp1[i]+","+dp2[i]);
max=Math.max(max,dp1[i]);
}
return max;
}
/**
// -2 2 3 -4
//dp1: 0 2 6 48
//dp2: -2 -4 -12 -24
//
// 2 -5 -2 -4 3
// 2 0 20 8 24
// 0 -10 -2 -80 -240
*/
不想解释太多,虽然过了,但是确实有点蠢
解法二
max[i],min[i] 代表的就是以nums[i] 结尾的最大乘积和最小乘积
public static int maxProduct(int[] nums) {
int[] min=new int[nums.length];
int[] max=new int[nums.length];
int res=max[0]=min[0]=nums[0];
for (int i=1;i<nums.length;i++) {
max[i]=Math.max(nums[i]*min[i-1],Math.max(nums[i],nums[i]*max[i-1]));
min[i]=Math.min(nums[i]*min[i-1],Math.min(nums[i],nums[i]*max[i-1]));
res=Math.max(res,max[i]);
}
return res;
}
为什么要记录最小乘积相信不需要我多说了吧,其实只要想清楚一点就 ok,每个位置的max[i]其实只有三种来源(纸上写写就明白了)
nums[i] >= 0并且max[i-1] > 0,max[i] = max[i-1] * nums[i]nums[i] >= 0并且max[i-1] < 0,此时如果和前边的数累乘的话,会变成负数,所以max[i] = nums[i]nums[i] < 0,如果是负数就不应该再和前面max[i]相乘,而是考虑min[i]当 min[i-1] < 0,max[i] = min[i-1] * nums[i]当 min[i-1] >= 0,max[i] = nums[i]
然后我们直接求这三种情况的最大值就 ok 了,不用考虑那些分支,我上面的第一种解法其实就是考虑了所有分支,结果才写出了那样的 dp, min[i] 的过程和上面一样,就不赘述
1567. 乘积为正数的最长子数组长度
Difficulty: 中等
给你一个整数数组 nums ,请你求出乘积为正数的最长子数组的长度。
一个数组的子数组是由原数组中零个或者更多个连续数字组成的数组。
请你返回乘积为正数的最长子数组长度。
示例 1:
输入:nums = [1,-2,-3,4]
输出:4
解释:数组本身乘积就是正数,值为 24 。
示例 2:
输入:nums = [0,1,-2,-3,-4]
输出:3
解释:最长乘积为正数的子数组为 [1,-2,-3] ,乘积为 6 。
注意,我们不能把 0 也包括到子数组中,因为这样乘积为 0 ,不是正数。
示例 3:
输入:nums = [-1,-2,-3,0,1]
输出:2
解释:乘积为正数的最长子数组是 [-1,-2] 或者 [-2,-3] 。
示例 4:
输入:nums = [-1,2]
输出:1
示例 5:
输入:nums = [1,2,3,5,-6,4,0,10]
输出:4
提示:
1 <= nums.length <= 10^5-10^9 <= nums[i] <= 10^9
解法一
一开始想歪了,和上面一题最开始一样写了个贼蠢的 dp,好在后面还是自己想出来了,下面的是后面想出来的简单解法
func getMaxLen(nums []int) int {
var n = len(nums)
//dp[i][0]:
var dp = make([][2]int, n+1)
var res = 0
for i := 1; i <= n; i++ {
if nums[i-1] > 0 {
dp[i][0] = dp[i-1][0] + 1
if dp[i-1][1] != 0 {
dp[i][1] = dp[i-1][1] + 1
}
} else if nums[i-1] < 0 {
if dp[i-1][1] != 0 {
dp[i][0] = dp[i-1][1] + 1
}
dp[i][1] = dp[i-1][0] + 1
}
if dp[i][0] > res {
res = dp[i][0]
}
}
return res
}
解法二
贼蠢的 DP,面向 case 编程
//垃圾 DP,面向 case 编程,没有 case 一辈子改不出来(居然还被我改对了)
//100+ms 时间复杂度 O(N^2),lc 的 case 没能卡掉,但是应该是可以构造出一组特殊 case 卡掉的,懒得想了
func getMaxLen(nums []int) int {
var n = len(nums)
var dp = make([]int, n+1)
if nums[0] > 0 {
dp[0] = 1
}
var res = dp[0]
for i := 1; i < n; i++ {
if nums[i] > 0 {
dp[i] = dp[i-1] + 1
} else if nums[i] < 0 {
if i-dp[i-1]-1 >= 0 && nums[i-dp[i-1]-1] < 0 {
dp[i] = dp[i-1] + 2
if i-dp[i-1]-2 >= 0 {
dp[i] += dp[i-dp[i-1]-2]
}
} else {
//从 i-dp[i-1] 开始找负数,然后从这个负数截断
var cnt = 0
for k := i-dp[i-1]; k < i; k++ {
if nums[k] < 0 {
dp[i] = dp[i-1]-cnt
break
}
cnt++
}
}
}
if dp[i] > res {
res = dp[i]
}
}
return res
}
1594. 矩阵的最大非负积
Difficulty: 中等
给你一个大小为 rows x cols 的矩阵 grid 。最初,你位于左上角 (0, 0) ,每一步,你可以在矩阵中 向右 或 向下 移动。
在从左上角 (0, 0) 开始到右下角 (rows - 1, cols - 1) 结束的所有路径中,找出具有 最大非负积 的路径。路径的积是沿路径访问的单元格中所有整数的乘积。
返回 最大非负积 对**10<sup>9</sup> + 7** 取余 的结果。如果最大积为负数,则返回-1 。
**注意,**取余是在得到最大积之后执行的。
示例 1:
输入:grid = [[-1,-2,-3],
[-2,-3,-3],
[-3,-3,-2]]
输出:-1
解释:从 (0, 0) 到 (2, 2) 的路径中无法得到非负积,所以返回 -1
示例 2:
输入:grid = [[1,-2,1],
[1,-2,1],
[3,-4,1]]
输出:8
解释:最大非负积对应的路径已经用粗体标出 (1 * 1 * -2 * -4 * 1 = 8)
示例 3:
输入:grid = [[1, 3],
[0,-4]]
输出:0
解释:最大非负积对应的路径已经用粗体标出 (1 * 0 * -4 = 0)
示例 4:
输入:grid = [[ 1, 4,4,0],
[-2, 0,0,1],
[ 1,-1,1,1]]
输出:2
解释:最大非负积对应的路径已经用粗体标出 (1 * -2 * 1 * -1 * 1 * 1 = 2)
提示:
1 <= rows, cols <= 15-4 <= grid[i][j] <= 4
解法一
和上面两题一样,非常套路的 DP,但是我一开始想把初始化给省掉,调了半天发现不太好搞。外围的 dp 取值会影响内部的取值,所以还是老老实实手动初始化,老是想偷懒有时候可能会适得其反(好未来笔试)
func maxProductPath(grid [][]int) int {
var m, n = len(grid), len(grid[0])
var MOD = int(1e9+7)
var dp = make([][][2]int, m)
var Max = func(a, b int) int {if a < b {return b}; return a}
var Min = func(a, b int) int {if a > b {return b}; return a}
for i := 0; i < m; i++ {
dp[i] = make([][2]int, n)
}
dp[0][0][1] = grid[0][0]
dp[0][0][0] = grid[0][0]
for i := 1; i < m; i++ {
dp[i][0][0] = grid[i][0] * dp[i-1][0][0]
dp[i][0][1] = dp[i][0][0]
}
for j := 1; j < n; j++ {
dp[0][j][0] = grid[0][j] * dp[0][j-1][0]
dp[0][j][1] = dp[0][j][0]
}
for i := 1; i < m; i++ {
for j := 1; j < n; j++ {
if grid[i][j] > 0 {
dp[i][j][0] = grid[i][j] * Max(dp[i][j-1][0], dp[i-1][j][0])
dp[i][j][1] = grid[i][j] * Min(dp[i][j-1][1], dp[i-1][j][1])
}else if grid[i][j] < 0 {
dp[i][j][0] = grid[i][j] * Min(dp[i][j-1][1], dp[i-1][j][1])
dp[i][j][1] = grid[i][j] * Max(dp[i][j-1][0], dp[i-1][j][0])
}
}
}
if dp[m-1][n-1][0] < 0 {
return -1
}
return dp[m-1][n-1][0] % MOD
}
221. 最大正方形
在一个由 0 和 1 组成的二维矩阵内,找到只包含 1 的最大正方形,并返回其面积。
示例:
输入:
1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0
输出:4
解法一
递推公式:dp[i][j]=1+min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1]) 有的类似短板理论,取决于最小的哪一个正方形
public int maximalSquare(char[][] matrix) {
if (matrix==null || matrix.length<=0) {
return 0;
}
int m=matrix.length;
int n=matrix[0].length;
//这里+1 处理边界
int[][] dp=new int[m+1][n+1];
int max=0;
for (int i=1;i<=m;i++) {
for (int j=1;j<=n;j++) {
if (matrix[i-1][j-1]=='1') {
dp[i][j]=1+Math.min(dp[i-1][j-1],Math.min(dp[i][j-1],dp[i-1][j]));
max=Math.max(max,dp[i][j]);
}
}
}
return max*max;
}
这题还有个需要注意的地方就是边界的处理,这里实现的代码中dp[i][j] 其实表示的是以 matrix[i-1][j-1] 作为右下角结尾的正方形的最大边长,这样的话就不用考虑上下两条边的边界 case,相当于在 dp 数组上下边界之外又加了一层 0
到这里我也大致明白了一些动态规划的题目的递推写法为都是从 1 开始了,比如上面的编辑距离
1277. 统计全为 1 的正方形子矩阵
给你一个 m * n 的矩阵,矩阵中的元素不是 0 就是 1,请你统计并返回其中完全由 1 组成的 正方形 子矩阵的个数。
示例 1:
输入:matrix =
[
[0,1,1,1],
[1,1,1,1],
[0,1,1,1]
]
输出:15
解释:
边长为 1 的正方形有 10 个。
边长为 2 的正方形有 4 个。
边长为 3 的正方形有 1 个。
正方形的总数 = 10 + 4 + 1 = 15.
示例 2:
输入:matrix =
[
[1,0,1],
[1,1,0],
[1,1,0]
]
输出:7
解释:
边长为 1 的正方形有 6 个。
边长为 2 的正方形有 1 个。
正方形的总数 = 6 + 1 = 7.
提示:
1 <= arr.length <= 3001 <= arr[0].length <= 3000 <= arr[i][j] <= 1
解法一
12.1 的周赛题目,其实先做的上面的最大正方形,然后发现这一题和上面的一样。
public int countSquares(int[][] matrix) {
if (matrix==null || matrix.length<=0) {
return 0;
}
int m=matrix.length;
int n=matrix[0].length;
int [][]dp=new int[m+1][n+1];
int res=0;
for (int i=1;i<=m;i++) {
for (int j=1;j<=n;j++) {
if (matrix[i-1][j-1]==1) {
dp[i][j]=Math.min(dp[i-1][j-1],Math.min(dp[i][j-1],dp[i-1][j]))+1;
res+=dp[i][j];
}
}
}
return res;
}
一摸一样,理解一点就 ok,以matrix[i][j] 为右下角的最大正方形的边长,就是以这个点为右下角的正方形的数量!!!
1139. 最大的以 1 为边界的正方形
Difficulty: 中等
给你一个由若干 0 和 1 组成的二维网格 grid,请你找出边界全部由 1 组成的最大 正方形 子网格,并返回该子网格中的元素数量。如果不存在,则返回 0。
示例 1:
输入:grid = [[1,1,1],[1,0,1],[1,1,1]]
输出:9
示例 2:
输入:grid = [[1,1,0,0]]
输出:1
提示:
1 <= grid.length <= 1001 <= grid[0].length <= 100grid[i][j]为0或1
解法一
这个题目还是挺有意思的,第一次看了以后没啥思路,看了题解对 dp 数组的的定义后就明白了,今天来实现下,WA 了 2 次,都 WA 的有理有据,很舒服,做这种题就很舒服
public int largest1BorderedSquare(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
//dp[i][j][0]: i,j 左边连续的 1 的个数
//dp[i][j][1]: i,j 上边连续的 1 的个数
int[][][] dp = new int[m+1][n+1][2];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (grid[i-1][j-1] == 1){
dp[i][j][0] = 1 + dp[i][j-1][0];
dp[i][j][1] = 1 + dp[i-1][j][1];
}
}
}
int res = 0;
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
//WA 点 2:最短的那条边不一定是边长,可以更短所以需要遍历所有小于最短边长的长度
//所以题目的数据范围是不会骗人的,给的 100 那么时间复杂度一定不是 N2 的
for (int side = Math.min(dp[i][j][0], dp[i][j][1]); side >= 1; side--){
//WA 点 1:大于等于
if (dp[i][j-side+1][1] >= side && dp[i-side+1][j][0] >= side){
res = Math.max(res, side);
break; //更短的就没必要考虑了
}
}
}
}
return res * res;
}
其实这个题目的关键就在于状态的定义,如何去构造一个正方形,一图胜千言(PPT 画图还是挺方便)
 (之前的图有点小问题,改了下)
(之前的图有点小问题,改了下)
求以某个点为右下角的正方形,首先我们考虑这个点为右下角可能构成的最大正方形边长是多大
很明显应该是该点左边和上边连续 1 个数的最小值,如上图的(6,5)点,最大的可能边长就应该是 6,然后我们枚举所有的小于等于 6 大于等于 1 的边长 side,验证 side 能否构成正方形
验证 side 是否合法也很容易,如上图,我们只需要考虑(6,5)上边距离为 side 的点的左边连续 1 的个数是否大于等于 side(dp[i-side+1][j][0] >= side),以及左边距离为 side 的点的上边连续的 1 的个数是否大于等于 side(dp[i][j-side+1][1] >= side),如果都大于等于 side 那么该 side 就是合法的,我们统计这些合法的 side 的最大值就 ok 了
在 lc 上水了一发 题解
44. 通配符匹配
给定一个字符串 (s) 和一个字符模式 (p) ,实现一个支持 ‘?’ 和 ‘*’ 的通配符匹配。
'?' 可以匹配任何单个字符。
'*' 可以匹配任意字符串(包括空字符串)。
两个字符串完全匹配才算匹配成功。
说明:
- s 可能为空,且只包含从 a-z 的小写字母。
- p 可能为空,且只包含从 a-z 的小写字母,以及字符 ? 和 *。
示例 1:
输入:
s = "aa"
p = "a"
输出:false
解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:
s = "aa"
p = "*"
输出:true
解释:'*' 可以匹配任意字符串。
示例 3:
输入:
s = "cb"
p = "?a"
输出:false
解释:'?' 可以匹配 'c', 但第二个 'a' 无法匹配 'b'。
示例 4:
输入:
s = "adceb"
p = "*a*b"
输出:true
解释:第一个 '*' 可以匹配空字符串,第二个 '*' 可以匹配字符串 "dce".
示例 5:
输入:
s = "acdcb"
p = "a*c?b"
输入:false
解法一
其实这题还有一道类似的题,10. 正则表达式生成 我放在回溯里了,因为 dp 的解法暂时还没花时间去看,感觉递归好理解一点,后面有时间再加进来
public boolean isMatch(String s, String p) {
//dp[i][j] 代表 s[0,i-1](s 的前 i 个字符),p[0,j-1](p 的前 j 个字符)是否匹配
boolean[][] dp=new boolean[s.length()+1][p.length()+1];
//dp[i][0]=false dp[0][j] p[j]=="*"|"?"
dp[0][0]=true;
for (int j=1;j<=p.length();j++) {
if (p.charAt(j-1)=='*') {
dp[0][j]=dp[0][j-1]; //dp[0][j]=true 是错的
}
}
//1. p[i]=p[j] dp[i][j]=dp[i-1][j-1]
//2. p[j]="?" dp[i][j]=dp[i-1][j-1]
//3. p[j]="*" dp[i][j]=dp[i-1][j] | dp[i][j-1]
for (int i=1;i<=s.length();i++) {
for (int j=1;j<=p.length();j++) {
if (s.charAt(i-1) == p.charAt(j-1) || p.charAt(j-1)=='?') {
dp[i][j]=dp[i-1][j-1];
}else if (p.charAt(j-1)=='*') { //abcd ab* | ab ab*
dp[i][j]=dp[i-1][j]|dp[i][j-1];
}
}
}
return dp[s.length()][p.length()];
}
思路都在注释里面了,比正则那个要简单,比较不好想的一点就是 dp[i][j]=dp[i-1][j]|dp[i][j-1]其实分别对应的就是 * 匹配任意字符的情况和匹配空字符的情况,匹配任意字符为什么不是dp[i-1][j-1]? 因为* 不仅仅只可以匹配一个字符,它可以匹配任意个数的任意字符,就比如这样的abcd,ab* 的,这种情况其实最终还是转换成了匹配空字符的情况,这也是动态规划的思想所在。
10. 正则表达式匹配
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s 的,而不是部分字符串。
说明:
- s 可能为空,且只包含从 a-z 的小写字母。
- p 可能为空,且只包含从 a-z 的小写字母,以及字符 . 和 *。
示例 1:
输入:
s = "aa"
p = "a"
输出:false
解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入:
s = "aa"
p = "a*"
输出:true
解释:因为 '*' 代表可以匹配零个或多个前面的那一个元素,在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入:
s = "ab"
p = ".*"
输出:true
解释:".*" 表示可匹配零个或多个('*')任意字符('.')。
示例 4:
输入:
s = "aab"
p = "c*a*b"
输出:true
解释:因为 '*' 表示零个或多个,这里 'c' 为 0 个,'a' 被重复一次。因此可以匹配字符串 "aab"。
示例 5:
输入:
s = "mississippi"
p = "mis*is*p*."
输出:false
解法一
dfs 回溯,暴力解法,挺难搞
public boolean isMatch(String s, String p) {
return match(s,0,p,0);
}
public boolean match(String s,int sIdx, String p,int pIdx) {
if (sIdx>=s.length() && pIdx>=p.length()) {
return true;
}
if (pIdx>=p.length()) {
return false;
}
//这里的判断其实不太对,也不能说不对,会稍微慢一点,因为题目中是不会给**这样的 case 的
//可以直接一次跳两步判断是不是*
if (sIdx == s.length()) {
//后面没有*的情况 aaa aaaa
if (pIdx==p.length()-1 && p.charAt(pIdx)!='*') { //p 也到尽头,并且不为*
return false;
}
while(pIdx<p.length()){ //p 没到尽头,检查后面的是否有两个连续的非*
if (p.charAt(pIdx) != '*' && (pIdx+1<p.length() && p.charAt(pIdx+1)!='*')) {
return false;
}
pIdx++;
}
//aaa aaa*c
return p.charAt(pIdx-1)=='*';
}
if (pIdx+1 < p.length() && p.charAt(pIdx+1) =='*') { //pIdx 下一个是 *
//*匹配至少一个
if ((s.charAt(sIdx) == p.charAt(pIdx) || p.charAt(pIdx)=='.') && match(s,sIdx+1,p,pIdx)) {
return true;
}
//*匹配 0 个
return match(s,sIdx,p,pIdx+2);
}else{
//pIdx 下一个不是*
if ((p.charAt(pIdx) == s.charAt(sIdx) || p.charAt(pIdx)=='.') && match(s,sIdx+1,p,pIdx+1)) {
return true;
}
return false;
}
}
这题还是挺麻烦的,毕竟是 hard 题,我也是看了题解才写出来,核心就是要把题目意思理解对,我这里没有做记忆化,懒得写
解法二
他来了他来了,他带着 dp 解法来了,终于还是把 dp 的解法补上来了,参考 题解 ,注意下标的转换,这里容易被绕进去,详细的都在注释中了
//update: 2020.4.12
public boolean isMatch(String text, String pattern) {
//dp[i][j] 代表 text[0,i) 和 pattern[0,j) 是否匹配
boolean[][] dp=new boolean[text.length()+1][pattern.length()+1];
//都为空的时候肯定是匹配的
dp[0][0]=true;
//pattern 为空,text 不为空肯定是无法匹配,默认 false, 不用处理
//text 为空,pattern 不为空需要额外判断
for(int i=2;i<=pattern.length();i++){
dp[0][i]=pattern.charAt(i-1)=='*'&&dp[0][i-2];
}
for(int i=1;i<=text.length();i++){
for(int j=1;j<=pattern.length();j++){
if(singleMatch(text,pattern,i-1,j-1)){
dp[i][j]=dp[i-1][j-1];
}else if(pattern.charAt(j-1)=='*'){
//j 一定是>=2 的,p 如果是*开头就是错误的语法,不过 lc 其实也没有这样的 case
if(j<2) return false;
//ab abb* --> '*'匹配 0 个 b
//abbbbb ab* --> '*'匹配多个 b
//注意 dp[i-1][j] 和 text.charAt(i-1) 的 i-1 含义是不一样的
//text.charAt(i-1) 的 i-1 其实指的是当前元素,而 dp[i-1][j] 中的 i-1 是前一个元素
//abc ab*
dp[i][j]=dp[i][j-2] || (singleMatch(text,pattern,i-1,j-2) && dp[i-1][j]);
}
}
}
return dp[text.length()][pattern.length()];
}
public boolean singleMatch(String s,String p,int i,int j){
return s.charAt(i)==p.charAt(j) || p.charAt(j)=='.';
}
果然还是动态规划简洁,而且搞懂之后也很好理解~~
1326. 灌溉花园的最少水龙头数目
在 x 轴上有一个一维的花园。花园长度为 n,从点 0 开始,到点 n 结束。
花园里总共有 n + 1 个水龙头,分别位于 [0, 1, …, n] 。
给你一个整数 n 和一个长度为 n + 1 的整数数组 ranges ,其中 ranges[i] (下标从 0 开始)表示:如果打开点 i 处的水龙头,可以灌溉的区域为 [i - ranges[i], i + ranges[i]] 。
请你返回可以灌溉整个花园的 最少水龙头数目 。如果花园始终存在无法灌溉到的地方,请你返回 -1 。
示例 1:
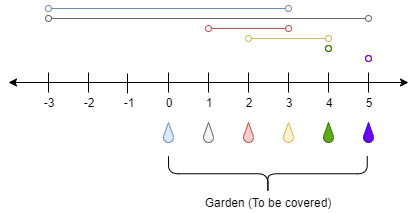
输入:n = 5, ranges = [3,4,1,1,0,0]
输出:1
解释:
点 0 处的水龙头可以灌溉区间 [-3,3]
点 1 处的水龙头可以灌溉区间 [-3,5]
点 2 处的水龙头可以灌溉区间 [1,3]
点 3 处的水龙头可以灌溉区间 [2,4]
点 4 处的水龙头可以灌溉区间 [4,4]
点 5 处的水龙头可以灌溉区间 [5,5]
只需要打开点 1 处的水龙头即可灌溉整个花园 [0,5] 。
示例 2:
输入:n = 3, ranges = [0,0,0,0]
输出:-1
解释:即使打开所有水龙头,你也无法灌溉整个花园。
示例 3:
输入:n = 7, ranges = [1,2,1,0,2,1,0,1]
输出:3
示例 4:
输入:n = 8, ranges = [4,0,0,0,0,0,0,0,4]
输出:2
示例 5:
输入:n = 8, ranges = [4,0,0,0,4,0,0,0,4]
输出:1
提示:
1 <= n <= 10^4ranges.length == n + 10 <= ranges[i] <= 100
解法一
172 周赛的最后一题
public int minTaps(int n, int[] ranges) {
int[] dp=new int[n+1]; //浇溉 i 位置前需要最少的水龙头
Arrays.fill(dp,Integer.MAX_VALUE);
dp[0]=0;
for (int i=0;i<=n;i++) {
int left=Math.max(0,i-ranges[i]);
int right=Math.min(n,i+ranges[i]);
if (dp[left]==Integer.MAX_VALUE) { //左边界不可达
continue;
}
for (int j=left+1;j<=right;j++) {
dp[j]=Math.min(dp[j],dp[left]+1); //范围内的区域 dp 值
}
}
return dp[n]==Integer.MAX_VALUE?-1:dp[n];
}
动态规划的解法,对每个水龙头所覆盖的区域进行递推,dp[i] 代表浇灌0 ~ i 位置区域所需要的最少的水头所以很容易得到递推公式dp[j]=Math.min(dp[j],dp[left]+1) ,整体还是很好理解的
解法二
贪心算法,和 贪心专题 中的 1024. 视频剪辑 是一样的题目
有时间再来补吧
1335. 工作计划的最低难度
你需要制定一份 d 天的工作计划表。工作之间存在依赖,要想执行第 i 项工作,你必须完成全部 j 项工作( 0 <= j < i)。
你每天 至少 需要完成一项任务。工作计划的总难度是这 d 天每一天的难度之和,而一天的工作难度是当天应该完成工作的最大难度。
给你一个整数数组 jobDifficulty 和一个整数 d,分别代表工作难度和需要计划的天数。第 i 项工作的难度是 jobDifficulty[i]。
返回整个工作计划的 最小难度 。如果无法制定工作计划,则返回 -1 。
示例 1:
输入:jobDifficulty = [6,5,4,3,2,1], d = 2
输出:7
解释:第一天,您可以完成前 5 项工作,总难度 = 6.
第二天,您可以完成最后一项工作,总难度 = 1.
计划表的难度 = 6 + 1 = 7
示例 2:
输入:jobDifficulty = [9,9,9], d = 4
输出:-1
解释:就算你每天完成一项工作,仍然有一天是空闲的,你无法制定一份能够满足既定工作时间的计划表。
示例 3:
输入:jobDifficulty = [1,1,1], d = 3
输出:3
解释:工作计划为每天一项工作,总难度为 3 。
示例 4:
输入:jobDifficulty = [7,1,7,1,7,1], d = 3
输出:15
解法一
173 周赛的最后一道 dp 题,事后一个小时左右独立的 ac,还是挺舒服的,希望以后能更快 ac
public int minDifficulty(int[] jobDifficulty, int d) {
int jlen=jobDifficulty.length;
if(jlen<d){
return -1;
}
//dp[i][j] 第 i 天完成前 j 项任务的最低难度
int[][] dp=new int[d][jlen];
for(int i=0;i<dp.length;i++){
Arrays.fill(dp[i],Integer.MAX_VALUE);
}
int max=0;
for(int j=0;j<jlen;j++){
max=Math.max(max,jobDifficulty[j]);
dp[0][j]=max;
}
for(int i=1;i<d;i++){
for(int j=0;j<jlen;j++){
for(int k=j-1;k>=i-1;k--){
dp[i][j]=Math.min(dp[i][j], dp[i-1][k]+maxDifficulty(jobDifficulty,k+1,j));
}
}
}
return dp[d-1][jlen-1];
}
public int maxDifficulty(int[] jobDifficulty,int left,int right){
int max=jobDifficulty[left];
for(int i=left;i<=right;i++){
max=Math.max(max,jobDifficulty[i]);
}
return max;
}
核心的递推公式: dp[i][j]=min(dp[i][j],dp[i-1][0~k]+max(k+1,j))
其实也不是一开始就想到了这个递推公式,首先需要确定的是用几维数组和递推数组的含义,这个题目两个变量:天数和工作量;所以应该是二维的结构,dp[i][j] 然后对应题目所要求的东西,其实就可以确定 dp 数组的含义
dp[i][j] 的含义是前i天完成前j项工作的最低难度,最后返回的结果就是dp[d-1][jlen-1]
但是上面这个解法时间复杂度比较高,O(dN^3),其实可以做一下预处理降低时间复杂度
解法二
预处理的地方也写成了动态规划 hahaha~ 其实就是求一个区间和
public int minDifficulty(int[] jobDifficulty, int d) {
int jlen=jobDifficulty.length;
if(jlen<d){
return -1;
}
//dp[i][j] 前 i 天完成前 j 项任务的最低难度
int[][] dp=new int[d][jlen];
for(int i=0;i<dp.length;i++){
Arrays.fill(dp[i],Integer.MAX_VALUE);
}
//预处理
int[][] maxRange=new int[jlen][jlen];
for(int i=0;i<jlen;i++){
maxRange[i][i]=jobDifficulty[i];
for (int j=i+1;j<jlen;j++) {
//这里也是个动态规划 hahaha~
maxRange[i][j]=Math.max(maxRange[i][j-1],jobDifficulty[j]);
}
}
for(int j=0;j<jlen;j++){
dp[0][j]=maxRange[0][j];
}
for(int i=1;i<d;i++){
for(int j=0;j<jlen;j++){
for(int k=j-1;k>=i-1;k--){ //注意这里 k>=i-1 的含义
dp[i][j]=Math.min(dp[i][j], dp[i-1][k]+maxRange[k+1][j]);
}
}
}
return dp[d-1][jlen-1];
}
这样时间复杂度就降低为O(dN^2) ,当然还是有一点不完美,就是对边界的处理可以通过对 dp 数组+1 来规避,这个问题我之前也说过,这我尝试改了下,没改好,不改了,哈哈哈~
5331. 跳跃游戏 V
给你一个整数数组 arr 和一个整数 d 。每一步你可以从下标 i 跳到:
i + x,其中i + x < arr.length 且 0 < x <= d。i - x,其中i - x >= 0 且 0 < x <= d。
除此以外,你从下标 i 跳到下标 j 需要满足:arr[i] > arr[j] 且 arr[i] > arr[k] ,其中下标 k 是所有 i 到 j 之间的数字(更正式的,min(i, j) < k < max(i, j))。
你可以选择数组的任意下标开始跳跃。请你返回你 最多 可以访问多少个下标。
请注意,任何时刻你都不能跳到数组的外面
示例 1:
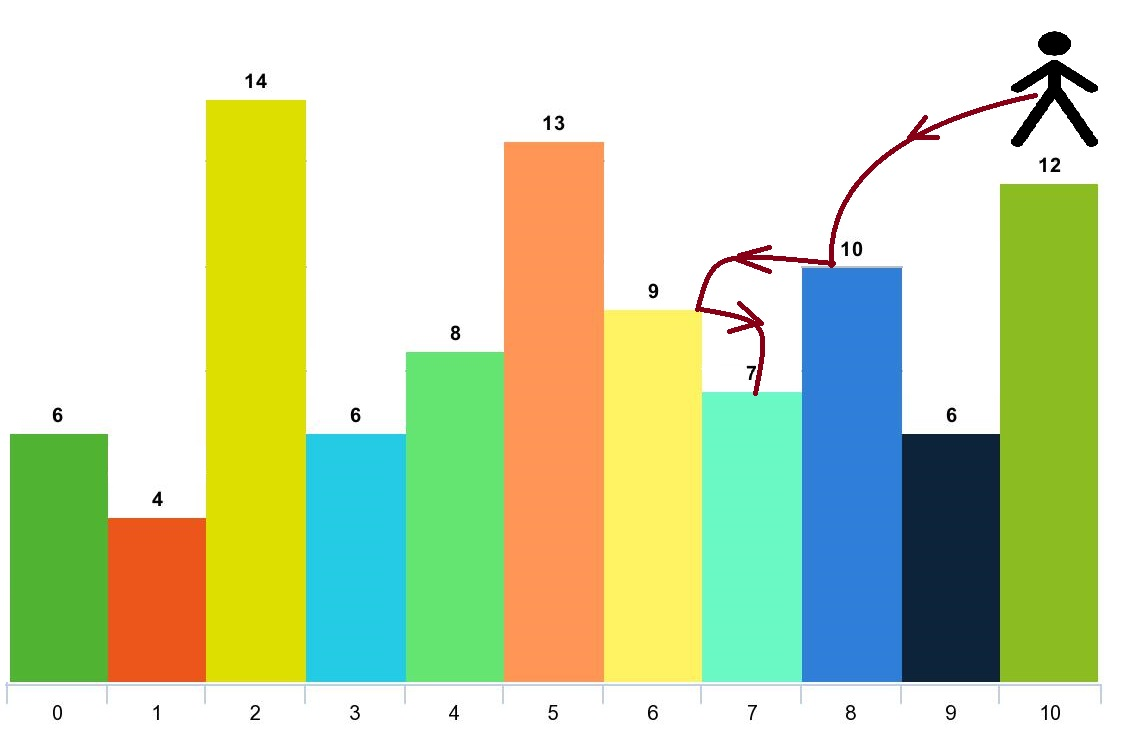
输入:arr = [6,4,14,6,8,13,9,7,10,6,12], d = 2
输出:4
解释:你可以从下标 10 出发,然后如上图依次经过 10 --> 8 --> 6 --> 7 。
注意,如果你从下标 6 开始,你只能跳到下标 7 处。你不能跳到下标 5 处因为 13 > 9 。你也不能跳到下标 4 处,因为下标 5 在下标 4 和 6 之间且 13 > 9 。
类似的,你不能从下标 3 处跳到下标 2 或者下标 1 处。
示例 2:
输入:arr = [3,3,3,3,3], d = 3
输出:1
解释:你可以从任意下标处开始且你永远无法跳到任何其他坐标。
示例 3:
输入:arr = [7,6,5,4,3,2,1], d = 1
输出:7
解释:从下标 0 处开始,你可以按照数值从大到小,访问所有的下标。
提示:
1 <= arr.length <= 10001 <= arr[i] <= 10^51 <= d <= arr.length
解法一
预处理+回溯+记忆化
private Integer[] cache=null;
public int maxJumps(int[] arr, int d) {
int[][] max=new int[arr.length][arr.length];
cache=new Integer[arr.length];
for (int i=0;i<arr.length;i++) {
max[i][i]=arr[i];
for (int j=i+1;j<arr.length;j++) {
max[i][j]=Math.max(max[i][j-1],arr[j]);
}
}
int res=0;
for (int i=0;i<arr.length;i++) {
res=Math.max(jump(arr,d,i,max),res);
}
return res+1;
}
public int jump(int[] arr,int d,int index,int[][] max){ //从 index 起跳能跳多远
if (cache[index]!=null) {
return cache[index];
}
int res=0;
for (int i=Math.max(index-d,0);i<index;i++) {
if (arr[index]>arr[i] && arr[index]>max[i+1][index-1]) {
res=Math.max(jump(arr,d,i,max)+1,res);
}
}
//index=0, i=1 , i<=1
for (int i=index+1;i<=Math.min(index+d,arr.length-1);i++) {
if (arr[index]>arr[i] && arr[index]>max[index+1][i-1]) {
res=Math.max(jump(arr,d,i,max)+1,res);
}
}
return cache[index]=res;
}
其实已经在超时的边缘了。没有必要做预处理,一开始被题括号里面的信息给迷惑了,不然也不会搞个预处理,其实题目的意思就是只能向低处跳,我开始还搞了两个区间值 haha,脑壳有点不亲白
解法二
改良后的回溯+记忆化
private Integer[] cache=null;
public int maxJumps(int[] arr, int d) {
cache=new Integer[arr.length];
int res=0;
for (int i=0;i<arr.length;i++) {
res=Math.max(jump(arr,d,i),res);
}
return res+1;
}
public int jump(int[] arr,int d,int index){
if (cache[index]!=null) {
return cache[index];
}
int res=0;
//挨个跳,有一个跳不到,后面所有的就都跳不到了
for (int i=index-1;i>=Math.max(index-d,0) && arr[index]>arr[i];i--) {
res=Math.max(jump(arr,d,i)+1,res);
}
for (int i=index+1;i<=Math.min(index+d,arr.length-1) && arr[index]>arr[i];i++) {
res=Math.max(jump(arr,d,i)+1,res);
}
return cache[index]=res;
}
解法三
自底向上动态规划
public int maxJumps(int[] arr, int d) {
int res=0,len=arr.length;
Pair[] pair=new Pair[len];
int[] dp=new int[len];
Arrays.fill(dp,1);
for (int i=0;i<len;i++) pair[i]=new Pair(i,arr[i]);
Arrays.sort(pair,(p1,p2)->p1.value-p2.value);
for (int i=0;i<len;i++) {
int index=pair[i].index;
//向左
for (int j=index-1;j>=Math.max(index-d,0) && arr[index]>arr[j];j--) {
dp[index]=Math.max(dp[j]+1,dp[index]);
}
//向右
for (int j=index+1;j<=Math.min(index+d,arr.length-1) && arr[index]>arr[j];j++) {
dp[index]=Math.max(dp[j]+1,dp[index]);
}
res=Math.max(dp[index],res);
}
return res;
}
class Pair{
int index;
int value;
public Pair(int index,int value){
this.index=index;
this.value=value;
}
}
这里其实动态规划还有麻烦一点,因为需要从高向低跳,所以我们需要先保证低处的 dp 值先计算完成,所以我们需要先排序,同时要保留原索引,所以我们需要建立一个Pair数组来辅助,跳的方式和上面回溯的一样
1262. 可被三整除的最大和
给你一个整数数组 nums,请你找出并返回能被三整除的元素最大和。
示例 1:
输入:nums = [3,6,5,1,8]
输出:18
解释:选出数字 3, 6, 1 和 8,它们的和是 18(可被 3 整除的最大和)。
示例 2:
输入:nums = [4]
输出:0
解释:4 不能被 3 整除,所以无法选出数字,返回 0。
示例 3:
输入:nums = [1,2,3,4,4]
输出:12
解释:选出数字 1, 3, 4 以及 4,它们的和是 12(可被 3 整除的最大和)。
提示:
1 <= nums.length <= 4 * 10^41 <= nums[i] <= 10^4
解法一
动态规划的解法,很久之前的一次周赛的题,好像是第一次双周赛的题?
public int maxSumDivThree(int[] nums) {
if (nums==null || nums.length<=0) {
return 0;
}
//dp[i][k] 0~i 之间/3 余 k 的最大元素和
int[][] dp=new int[nums.length+1][3];
dp[0][0]=0; //初始状态定义
dp[0][1]=Integer.MIN_VALUE;
dp[0][2]=Integer.MIN_VALUE;
for (int i=1;i<=nums.length;i++) {
if (nums[i-1]%3==0) {
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][0]+nums[i-1]);
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][1]+nums[i-1]);
dp[i][2]=Math.max(dp[i-1][2],dp[i-1][2]+nums[i-1]);
}
if (nums[i-1]%3==1) {
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][2]+nums[i-1]);
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]+nums[i-1]);
dp[i][2]=Math.max(dp[i-1][2],dp[i-1][1]+nums[i-1]);
}
if (nums[i-1]%3==2) {
dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+nums[i-1]);
dp[i][1]=Math.max(dp[i-1][1],dp[i-1][2]+nums[i-1]);
dp[i][2]=Math.max(dp[i-1][2],dp[i-1][0]+nums[i-1]);
}
}
return Math.max(0,dp[nums.length][0]);
}
看一下数据的范围40000,所以时间复杂度肯定是O(N) 或O(NlogN)的,O(N^2)的肯定超时啦
想了很久没想出来,然后瞄了一眼评论区,发现 dp 数组定义的是和余数相关的,然后就反应过来了,余 0 余 1 余 2, 他们的组合就可以得到新的最大余数和,我们最后要求的就是最后[0,nums.length] 余数为 0 的最大和
递推公式就不用多说了,看代码就行了,递推公式很容易得到,关键就是初始的状态定义,第一步的递推,我一开始没有设置边界,直接开始 dp 然后后面怎么改都不对,一开始定义的 base dp
dp[0][0]=nums[0]%3==0?nums[0]:Integer.MIN_VALUE;
dp[0][1]=nums[0]%3==1?nums[0]:Integer.MIN_VALUE;
dp[0][2]=nums[0]%3==2?nums[0]:Integer.MIN_VALUE;
然后过了几十后卡在了个 case 上
[2,19,6,16,5,10,7,4,11,6]
递推到第二个其实就有问题了
0 1 2
2 MIN MIN 2
19 21 MIN+19 2
这里的 19 的 1 明显应该就是 19,这里直接根据dp[i-1][1]+19递推得到的,后面的肯定都不对了,那我们这里将初始值设置为 0 可以么?
dp[0][0]=nums[0]%3==0?nums[0]:0;
对这个 case 确实可以,但是对于其他的就不对了,这容易想到,你设置为 0 下一层的 dp 值就可以从这个值递推过来,但是这明显是不对的,举个例子: 3,4 你将第一个 3 的余 2 最大值设置为 0,那么下一个 4 就可以通过上一个余 2 的最大值来更新当前的余 0 最大值,变成 4,这很明显就不对了,4 根本就不能被 3 整除
所以这里我们最好的处理方式是添加一个边界,相当于在数组的最前面添加一个 0,0%3=0
然后我们只需要将dp[0][0]设置为 0 就可以了,而 1 和 2 就设置为INT_MIN,让下一层不能通它来转移
dp 边界的处理方式还是要多练啊
解法二
优化空间为 O(1)
public int maxSumDivThree2(int[] nums) {
int[] dp=new int[3];
dp[1]=Integer.MIN_VALUE;
dp[2]=Integer.MIN_VALUE;
for (int i=1;i<=nums.length;i++) {
if (nums[i-1]%3==0) {
dp[0]=Math.max(dp[0],dp[0]+nums[i-1]);
dp[1]=Math.max(dp[1],dp[1]+nums[i-1]);
dp[2]=Math.max(dp[2],dp[2]+nums[i-1]);
}
if (nums[i-1]%3==1) {
int temp0=dp[0];
dp[0]=Math.max(dp[0],dp[2]+nums[i-1]);
dp[2]=Math.max(dp[2],dp[1]+nums[i-1]); //按依赖关系调整顺序,减少变量
dp[1]=Math.max(dp[1],temp0+nums[i-1]);
}
if (nums[i-1]%3==2) {
int temp0=dp[0];
dp[0]=Math.max(dp[0],dp[1]+nums[i-1]);
dp[1]=Math.max(dp[1],dp[2]+nums[i-1]);
dp[2]=Math.max(dp[2],temp0+nums[i-1]);
}
}
return dp[0];
}
可以看出代码还是可以简化的很短的,为了表达的清晰就不改了
解法三
贪心,放在 贪心专题 中
面试题 60. n 个骰子的点数
把 n 个骰子扔在地上,所有骰子朝上一面的点数之和为 s。输入 n,打印出 s 的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n 个骰子所能掷出的点数集合中第 i 小的那个的概率。
示例 1:
输入:1
输出:[0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]
示例 2:
输入:2
输出:[0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]
限制:
1 <= n <= 11
解法一
很有意思的题,看返回值还不容易想到用动态规划
public double[] twoSum(int n) {
//dp[i][j] 代表 i 枚色子和为 j 的概率
double[][] dp=new double[n+1][6*n+1];
double probability=1.0/6.0;
//base 初始化
for(int i=1;i<=6;i++) dp[1][i]=probability;
for(int i=2;i<=n;i++){ //枚举色子
for(int j=i;j<=i*6;j++){ //枚举点数
for(int k=1;k<=j && k<=6;k++){ //枚举当前色子的点数
dp[i][j]+=(probability*dp[i-1][j-k]);
}
}
}
double[] res=new double[5*n+1];//
System.arraycopy(dp[n],n,res,0,res.length);
return res;
}
dp[i][j]代表** i 枚色子和为 j **的概率 递推公式很容易想到 dp[i][j]= 1/6(dp[i-1][j-1]+dp[i-1][j-2]+dp[i-1][j-3]...dp[i-1][j-6]) 然后我们枚举各个状态就 ok 了
264. 丑数 II
编写一个程序,找出第 n 个丑数。
丑数就是只包含质因数 2, 3, 5 的正整数。
示例:
输入:n = 10
输出:12
解释:1, 2, 3, 4, 5, 6, 8, 9, 10, 12 是前 10 个丑数。
说明:
- 是丑数。
- n 不超过 1690。
解法一
小根堆,将 base 每次乘 2 乘 3 乘 5 的结果放入小根堆,然后将堆顶拿出来 base,继续重复这个过程,中间要注意去重
public int nthUglyNumber3(int n) {
PriorityQueue<Long> queue=new PriorityQueue<>();
n-=1;
long base=1;
while(n-- >0){
queue.add(base*2);
queue.add(base*3);
queue.add(base*5);
base=queue.poll();
//去重
while(!queue.isEmpty()&&base==queue.peek()){
queue.poll();
}
}
return (int)base;
}
用HashSet去重
public int nthUglyNumber(int n) {
PriorityQueue<Long> queue=new PriorityQueue<>();
HashSet<Long> set=new HashSet<>();
long base=1;
long[] ugly={2,3,5};
n-=1;
set.add(1L);
while(n-->0){
for(int i=0;i<3;i++){
if (!set.contains(ugly[i]*base)) {
queue.add(ugly[i]*base);
set.add(ugly[i]*base);
}
}
base=queue.poll();
}
return (int)base;
}
解法二
这个解法还是很有技巧性的,其实就是按顺序生成丑数,一开始观察的时候就发现了但是确实想不到三指针的解法
public int nthUglyNumber4(int n) {
int[] dp=new int[n];
dp[0]=1;
int index1=0,index2=0,index3=0;
for (int i=1;i<n;i++) {
dp[i]=Math.min(dp[index1]*2,Math.min(dp[index2]*3,dp[index3]*5));
index1+=(dp[index1]*2==dp[i]?1:0);
index2+=(dp[index2]*3==dp[i]?1:0);
index3+=(dp[index3]*5==dp[i]?1:0);
}
return dp[n-1];
}
面试题 62. 圆圈中最后剩下的数字
0,1,,n-1 这 n 个数字排成一个圆圈,从数字 0 开始,每次从这个圆圈里删除第 m 个数字。求出这个圆圈里剩下的最后一个数字。
例如,0、1、2、3、4 这 5 个数字组成一个圆圈,从数字 0 开始每次删除第 3 个数字,则删除的前 4 个数字依次是 2、0、4、1,因此最后剩下的数字是 3。
示例 1:
输入:n = 5, m = 3
输出:3
示例 2:
输入:n = 10, m = 17
输出:2
限制:
- 1 <= n <= 10^5
- 1 <= m <= 10^6
解法一
用链表模拟的解法,在数据太大的时候会 TLE
/*
链表模拟解法
0 1 2 3 4 5 m=3
3 4 5 0 1
*/
public int lastRemaining(int n, int m) {
Deque<Integer> queue=new LinkedList<>();
for(int i=0;i<n;i++)
queue.addLast(i);
while(queue.size()>1){
for(int i=0;i<m;i++){
int temp=queue.removeFirst();
if(i!=m-1){
queue.addLast(temp);
}
}
}
return queue.getFirst();
}
解法二
数学归纳法,加上一点递推 dp
/*
0 ~ n-1 每次 kill 第 k 个人
k=(m-1)%n
kill k 之后,在 n-1 个人中重建新索引
原始索引 新的 index
k+1 0
k+2 1
k+3 2
... ...
n-1 n-k-2
0 n-k-1
1 n-k
2 n-k+1
... ...
k-1 n-2
新索引 (x) ---> 原始索引 (y)
y=(x+k+1)%n eg. (n-2+k+1)%n=(n+k-1)%n=k-1
设在 n-1 个人中最后剩下的人是 f(n-1,m) 按照上面的公式转换成原始索引就是
f(n,m)=(f(n-1,m)+k+1)%n
*/
//数学解法
public int lastRemaining(int n, int m) {
int last=0;//一个人的时候存活者 index f(1,m)=0
for(int i=2;i<=n;i++){ //枚举人数
last=(last+m)%i;
}
return last;
}
参考了 LeetCode 的 大佬题解,讲的挺好的
递归解法
//递归的挺好理解
public int lastRemaining(int n, int m) {
if(n==0) return 0;
return (lastRemaining(n-1,m)+m)%n;
}
1014. 最佳观光组合
给定正整数数组 A,A[i] 表示第 i 个观光景点的评分,并且两个景点 i 和 j 之间的距离为 j - i。
一对景点(i < j)组成的观光组合的得分为(A[i] + A[j] + i - j):景点的评分之和减去它们两者之间的距离。
返回一对观光景点能取得的最高分。
示例:
输入:[8,1,5,2,6]
输出:11
解释:i = 0, j = 2, A[i] + A[j] + i - j = 8 + 5 + 0 - 2 = 11
提示:
2 <= A.length <= 500001 <= A[i] <= 1000
解法一
暴力解法,O(N^2),这题数据 5w,肯定会 T
//A[i] + A[j] + i - j (i<j)
public int maxScoreSightseeingPair(int[] A) {
int res=-1;
for (int i=0;i<A.length;i++) {
for (int j=i+1;j<A.length;j++) {
res=Math.max(A[i]+A[j]+i-j,res);
}
}
return res;
}
解法二
// A[i]+A[j] - (j-i) i<j
// A[i]+i + (A[j]-j)
public int maxScoreSightseeingPair(int[] A) {
int res=-1;
int maxPre=A[0]+0;
for (int j=1;j<A.length;j++) {
res=Math.max(maxPre+A[j]-j,res);
maxPre=Math.max(maxPre,A[j]+j);
}
return res;
}
我们把式子合并一下 (A[i]+i)+(A[j]-j) ,然后发现其实上面的暴力解法中,我们想要结果最大实际上就是要两部分都最大,然后内层循环里面,A[j]-j 是个变量,而A[i]+i不变的,代表j位置之前,所有的A[i]+i 但是我们只需要最大的,所以我们完全可以用一个变量来保存这个最大值,然后遍历的过程中不断的更新它就 ok 了
983. 最低票价
在一个火车旅行很受欢迎的国度,你提前一年计划了一些火车旅行。在接下来的一年里,你要旅行的日子将以一个名为 days 的数组给出。每一项是一个从 1 到 365 的整数。
火车票有三种不同的销售方式:
- 一张为期一天的通行证售价为
costs[0]美元; - 一张为期七天的通行证售价为
costs[1]美元; - 一张为期三十天的通行证售价为
costs[2]美元。
通行证允许数天无限制的旅行。 例如,如果我们在第 2 天获得一张为期 7 天的通行证,那么我们可以连着旅行 7 天:第 2 天、第 3 天、第 4 天、第 5 天、第 6 天、第 7 天和第 8 天。
返回你想要完成在给定的列表 days 中列出的每一天的旅行所需要的最低消费。
示例 1:
输入:days = [1,4,6,7,8,20], costs = [2,7,15]
输出:11
解释:
例如,这里有一种购买通行证的方法,可以让你完成你的旅行计划:
在第 1 天,你花了 costs[0] = $2 买了一张为期 1 天的通行证,它将在第 1 天生效。
在第 3 天,你花了 costs[1] = $7 买了一张为期 7 天的通行证,它将在第 3, 4, ..., 9 天生效。
在第 20 天,你花了 costs[0] = $2 买了一张为期 1 天的通行证,它将在第 20 天生效。
你总共花了 $11,并完成了你计划的每一天旅行。
示例 2:
输入:days = [1,2,3,4,5,6,7,8,9,10,30,31], costs = [2,7,15]
输出:17
解释:
例如,这里有一种购买通行证的方法,可以让你完成你的旅行计划:
在第 1 天,你花了 costs[2] = $15 买了一张为期 30 天的通行证,它将在第 1, 2, ..., 30 天生效。
在第 31 天,你花了 costs[0] = $2 买了一张为期 1 天的通行证,它将在第 31 天生效。
你总共花了 $17,并完成了你计划的每一天旅行。
提示:
1 <= days.length <= 3651 <= days[i] <= 365days按顺序严格递增costs.length == 31 <= costs[i] <= 1000
解法一
这题的递推关系其实很容易就想到:dp[i]=Min(dp[i-dt[k]]+costs[k],dp[i]),可是菜鸡的我还是搞了半天才 AC
public int mincostTickets(int[] days, int[] costs) {
int n=days.length;
int[] dp=new int[days[n-1]+1];
boolean[] visit=new boolean[days[n-1]+1];
for (int i:days) {
visit[i]=true;
}
Arrays.fill(dp,0x3f3f3f3f);
int [] dt = {1,7,30};
dp[days[0]-1]=0;//初始状态
//枚举所有的 day
for (int d=days[0];d<=days[n-1];d++) {
//一开始没想到这里,dubug 的时候才看出来,不在旅游计划中的应该直接延续前面的
if (!visit[d]) {
dp[d]=dp[d-1];
continue;
}
//三种票
for (int k=0;k<3;k++) {
dp[d]=Math.min((d-dt[k]>=days[0]-1?dp[d-dt[k]]:0)+costs[k],dp[d]);
}
}
return dp[days[n-1]];
}
一开始写了二维的,然后发现一维的状态并没有用,改成一维之后又 dubug 了半天,主要就在那个非旅行计划中的d没处理好,这题的状态定义不是特别清晰,然后搞混了,把非旅行计划内的也算进去了
837. 新 21 点
爱丽丝参与一个大致基于纸牌游戏 “21 点” 规则的游戏,描述如下:
爱丽丝以 0 分开始,并在她的得分少于 K 分时抽取数字。 抽取时,她从 [1, W] 的范围中随机获得一个整数作为分数进行累计,其中 W 是整数。 每次抽取都是独立的,其结果具有相同的概率。
当爱丽丝获得不少于 K 分时,她就停止抽取数字。 爱丽丝的分数不超过 N 的概率是多少?
示例 1
输入:N = 10, K = 1, W = 10
输出:1.00000
说明:爱丽丝得到一张卡,然后停止。
示例 2
输入:N = 6, K = 1, W = 10
输出:0.60000
说明:爱丽丝得到一张卡,然后停止。
在 W = 10 的 6 种可能下,她的得分不超过 N = 6 分。
示例 3
输入:N = 21, K = 17, W = 10
输出:0.73278
提示:
0 <= K <= N <= 100001 <= W <= 10000- 如果答案与正确答案的误差不超过
10^-5,则该答案将被视为正确答案通过。 - 此问题的判断限制时间已经减少。
解法一
题目意思都得理解好久,面试应该不会考,参考评论区大佬题解写的一个类似背包的做法
public double new21Game(int N, int K, int W) {
if(K==0) return 1;
//随机抽牌和为 i 的概率,背包问题
double[] dp=new double[N+1];
dp[0]=1;
dp[1]=1.0/W;
// i<=K
//dp[i] = 1/W(dp[i-1]+dp[i-2]+...+dp[i-W]);
//dp[i-1] = 1/W(dp[i-2]+dp[i-3]+...+dp[i-W-1])
//==> dp[i]=(1 + 1/W)*dp[i-1]-(1/W)*dp[i-W-1]
for(int i=2;i<=K;i++){
if(i-W-1>=0){
dp[i]=(1+1.0/W)*dp[i-1]-1.0/W*dp[i-W-1];
}else{
dp[i]=(1+1.0/W)*dp[i-1];
}
}
// i>K 从 i-W ~ i 区间选小于 K 的部分
//和剑指 offer 的骰子哪一题有点像
//dp[i] = 1/W(dp[K-1]+dp[K-2]+...+dp[i-W]) or dp[i]=1/W(dp[i-W]+dp[i-W+1]+..+dp[K-1])
//dp[i-1] = 1/W(dp[k-1]+dp[K-2]+...+dp[i-W-1]) or dp[i+1] = 1/W(dp[i-W+1]+dp[i-W+2]...+dp[K-1])
//==> dp[i] = dp[i-1]-1/W*dp[i-W-1] or dp[i]=1/W*dp[i-W]+dp[i+1] 两个是等价的
for (int i=K+1;i<=N;i++) {
if(i-W-1>=0){
dp[i]=dp[i-1]-1.0/W*dp[i-W-1];
}else{
dp[i]=dp[i-1]; //1/W
}
}
double res=0;
for (int i=K;i<=N;i++) {
res+=dp[i];
}
return res;
}
下一次碰到就不一定会做了,理解的不是很透彻,不过对背包公式的推导倒是理解多了一点
329. 矩阵中的最长递增路径
Difficulty: 困难
给定一个整数矩阵,找出最长递增路径的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你不能在对角线方向上移动或移动到边界外(即不允许环绕)。
示例 1:
输入:nums =
[
[9,9,4],
[6,6,8],
[2,1,1]
]
输出:4
解释:最长递增路径为 [1, 2, 6, 9]。
示例 2:
输入:nums =
[
[3,4,5],
[3,2,6],
[2,2,1]
]
输出:4
解释:最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
解法一
记忆化递归,这题如果递推的话需要保证子问题都已经被计算过,所以需要进行排序预处理,确保大的先求出来,然后再进行转移,参考上面 5331-跳跃游戏-V
int [][] dir ={{1, 0}, {0, 1}, {-1, 0}, {0, -1}};
Integer [][] cache = null;
//记忆化递归,数组递推的方式状态转移方向不明确,需要排序
public int longestIncreasingPath(int[][] matrix) {
if (matrix == null || matrix.length <=0){
return 0;
}
int m = matrix.length;
int n = matrix[0].length;
cache = new Integer[m][n];
int res = 0;
for(int i = 0; i < m; i++){
for(int j = 0; j < n; j++){
res = Math.max(res, dfs(matrix, i, j));
}
}
return res;
}
public int dfs(int[][] matrix, int x, int y){
if (cache[x][y] != null){
return cache[x][y];
}
int res = 1;
for (int i = 0; i < dir.length; i++){
int nx = x + dir[i][0];
int ny = y + dir[i][1];
if (valid(matrix, nx, ny) && matrix[nx][ny] > matrix[x][y]){
res = Math.max(res, dfs(matrix, nx, ny)+1);
}
}
return cache[x][y] = res;
}
public boolean valid(int[][] matrix, int x, int y){
return x >= 0 && x < matrix.length && y >= 0 && y < matrix[0].length;
}
字符串类型的动态规划
1143. 最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。 例如,“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。 若这两个字符串没有公共子序列,则返回 0
最长公共子序列问题是在一组序列(通常 2 个)中找到最长公共子序列(注意:不同于子串,LCS 不需要是连续的子串)。该问题是典型的计算机科学问题,是文件差异比较程序的基础,在生物信息学中也有所应用
示例 1:
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace",它的长度为 3。
示例 2:
输入:text1 = "abc", text2 = "abc"
输出:3
解释:最长公共子序列是 "abc",它的长度为 3。
示例 3:
输入:text1 = "abc", text2 = "def"
输出:0
解释:两个字符串没有公共子序列,返回 0。
解法一
2019.10.19 力扣终于有这题了,重新来做一遍,这题也就是经常说的 LCS,dp 的经典问题
public int longestCommonSubsequence(String A, String B) {
int[][] dp=new int[A.length()+1][B.length()+1];
for (int i=1;i<=A.length();i++) {
for (int j=1;j<=B.length();j++) {
if (A.charAt(i-1)==B.charAt(j-1)) {
dp[i][j]=dp[i-1][j-1]+1;
}else{
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[A.length()][B.length()];
}
其实看见这种什么最长的多半和 dp 有关系,这题只要明白几个要点就可以推出 dp 方程
-
dp[i][j]代表 A 序列前i个字符(记为Ai), 和 B 序列前j个字符(记为Bj) 的 LCS -
两层 for 循环遍历两个序列,当
A[i]==B[j]的时候,LCS 长度就会增加 1,进而得到 dp 方程dp[i][j]=dp[i-1][j-1]+1dp[i-1] [j-1] 代表的就是不包含Ai/Bj的Ai-1和Bj-1的 LCS -
A[i]!=B[j]的时候就有两种情况了,首先A[i]和B[j]已经不可能同时出现在最终的 LCS 里面了,所以我们考虑另外的两种情况dp[i][j-1]和dp[i-1][j]取个最大值
除此之外,还有一个值得注意的小细节,这里循环都是从 1 开始的,这样就不用处理初始值,如果从 0 开始的话,处理初始情况(i,j=0 的情况)会麻烦一点
解法二
2019.10.19 重写了一种记忆化递归的方法,没有 dp 快,但是思路其实是类似的
Integer[][] cache=null;
public int longestCommonSubsequence(String text1, String text2) {
if(text2==null || text1==null || text1.length()<=0 ||text2.length()<=0){
return 0;
}
int len1=text1.length();
int len2=text2.length();
cache=new Integer[len1][len2];
return lcs(text1,len1-1,text2,len2-1);
}
//lcs 定义:求 text1[0,a] 和 text2[0,b] 的最长公共子序列
public int lcs(String text1, int a,String text2,int b) {
if(a==-1 || b==-1){
return 0;
}
if (cache[a][b]!=null) {
return cache[a][b];
}
if (text1.charAt(a)==text2.charAt(b)) {
cache[a][b]=lcs(text1,a-1,text2,b-1)+1;
return cache[a][b];
}else{
cache[a][b]=Math.max(lcs(text1,a-1,text2,b),lcs(text1,a,text2,b-1));
return cache[a][b];
}
}
AtCoder-LCS
题目就不 copy 了,这里就是求出 lcs 具体的字符串,而不是求长度
我这里是参考了 leetcode 上一个大佬的 文章 利用 back 数组,从后向前递推,但是实际上有点多余,直接根据 dp 数组也可以推回去,但是这样写比较通用,逻辑比较清楚。
public static void main(String[] args) {
Scanner sc=new Scanner(System.in);
while(sc.hasNext()){
String A=sc.next();
String B=sc.next();
System.out.println(longestCommonSubsequence(A,B));
}
}
public static String longestCommonSubsequence(String A, String B) {
int lenA=A.length();
int lenB=B.length();
int[][] dp=new int[lenA+1][lenB+1];
int[][] back=new int[lenA+1][lenB+1];
for (int i=1;i<=lenA;i++) {
for (int j=1;j<=lenB;j++) {
if (A.charAt(i-1)==B.charAt(j-1)) {
dp[i][j]=dp[i-1][j-1]+1;
back[i][j]=1; //左上
}else if(dp[i-1][j]>dp[i][j-1]){
dp[i][j]=dp[i-1][j];
back[i][j]=2; //上
}else{
dp[i][j]=dp[i][j-1];
back[i][j]=0; //左
}
}
}
int i=lenA,j=lenB;
StringBuilder res=new StringBuilder();
while(i>0 && j>0){
if (back[i][j]==1) {
i--;j--;
res.append(A.charAt(i));
}else if(back[i][j]==2){
i--;
}else{
j--;
}
}
return res.reverse().toString();
}
了解即可。
718. 最长重复子数组
给两个整数数组 A 和 B ,返回两个数组中公共的、长度最长的子数组的长度。
示例 1:
输入:
A: [1,2,3,2,1]
B: [3,2,1,4,7]
输出:3
解释:
长度最长的公共子数组是 [3, 2, 1]。
说明:
- 1 <= len(A), len(B) <= 1000
- 0 <= A[i], B[i] < 100
解法一
简单的递推,注意别写成上面的 lcs 了,这里的dp[i][j] 代表的其实是公共子串以A[i]和B[i] 结尾的最长重复子数组长度,如果A[i]和B[i]不相等那就是 0
public int findLength(int[] A, int[] B) {
int lenA=A.length;
int lenB=B.length;
int[][] dp=new int[lenA+1][lenB+1];
int res=0;
for(int i=1;i<=lenA;i++){
for(int j=1;j<=lenB;j++){
if(A[i-1]==B[j-1]){
dp[i][j]=dp[i-1][j-1]+1;
res=Math.max(dp[i][j],res);
}
}
}
return res;
}
解法二
本来是想练练二分,在二分的 tag 里面看见的这题,结果发现这题 dp 似乎更容易,看了官方的二分的解法,其实就是二分公共子串的长度,然后检查,检查这一步有一些操作,不是很理解,以后有机会再来补充。 已补充,见 Rabin-Karp 专题
72. 编辑距离
给定两个单词 word1 和 word2,计算出将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
- 插入一个字符
- 删除一个字符
- 替换一个字符
示例 1:
输入:word1 = "horse", word2 = "ros"
输出:3
解释:
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')
示例 2:
输入:word1 = "intention", word2 = "execution"
输出:5
解释:
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')
解法一
很经典的动态规划的问题,做之前看了动态规划的思路,然后很快写出了递归的解法。
Integer[][] cache=null;
public int minDistance(String word1, String word2) {
cache=new Integer[word1.length()][word2.length()];
return minDistance(word1,word1.length()-1,word2,word2.length()-1);
}
//递归的定义:word1[0,idx1] 和 word2[0,idx2] 的最短编辑距离
public int minDistance(String word1,int idx1,String word2,int idx2) {
if (idx1<0) {
return idx2+1;
}
if (idx2<0) {
return idx1+1;
}
if (cache[idx1][idx2]!=null) {
return cache[idx1][idx2];
}
if (word1.charAt(idx1) == word2.charAt(idx2)) {
return cache[idx1][idx2]=minDistance(word1,idx1-1,word2,idx2-1);
}else{
return cache[idx1][idx2]=1+Math.min(minDistance(word1,idx1-1,word2,idx2),Math.min(minDistance(word1,idx1,word2,idx2-1),minDistance(word1,idx1-1,word2,idx2-1)));
}
}
核心的递推公式就是
minDis(i,j)=minDis(i-1,j-1) word1[i]==word2[j]
minDis(i,j)=min(minDis(i-1,j),minDis(i,j-1),minDis(i-1,j-1))+1 word1[i]!=word2[j]
第一个公式好说,相等时候就别动,延续之前的状态,关键是第二个,不相等的时候,简单来说就是求对应的三种操作增,删,改的最小值,但是这里,第二种删的操作,这里要想清楚,其实 word1 删除一个其实就等价于 word2 增加一个,所以是minDis(i,j-1),虽然题目说的是从 word1 转换为 word2,但是其实结果都是一样的,这个转换的过程其实是可逆的
解法二
标准的动态规划写法,感觉还是上面的记忆化递归好写,动态规划要考虑的边界比递归要多
public int minDistance2(String word1, String word2) {
if (word1.length()<=0 || word2.length()<=0) {
return word2.length()==0?word1.length():word2.length();
}
//dp[i][j]: word1 前 i 个和 word2 前 j 个的最短编辑距离
int[][] dp=new int[word1.length()+1][word2.length()+1];
for (int i=1;i<=word2.length();i++) {
dp[0][i]=i;
}
for (int i=1;i<=word1.length();i++) {
dp[i][0]=i;
}
for (int i=1; i<=word1.length();i++) {
for (int j=1;j<=word2.length();j++) {
if (word1.charAt(i-1)==word2.charAt(j-1)) {
dp[i][j]=dp[i-1][j-1];
}else{
dp[i][j]=1+Math.min(dp[i-1][j],Math.min(dp[i][j-1],dp[i-1][j-1]));
}
}
}
return dp[word1.length()][word2.length()];
}
647. 回文子串
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被计为是不同的子串。
示例 1:
输入:"abc"
输出:3
解释:三个回文子串:"a", "b", "c".
示例 2:
输入:"aaa"
输出:6
说明:6 个回文子串:"a", "a", "a", "aa", "aa", "aaa".
注意:
- 输入的字符串长度不会超过 1000。
解法一
动态规划的解法,其实我是没想到的,dp[i][j]代表的是s[i,j] 是不是回文子串
public int countSubstrings(String s) {
if (s==null || s.length()<=0) {
return 0;
}
int n=s.length();
//aaaba
//dp[i][j] i~j 是不是回文
boolean [][] dp=new boolean[n][n];
int res=n; //下面的循环没有统计单个字符的情况
for (int i=n-1;i>=0;i--) {
for (int j=i+1;j<n;j++) { //统一写法,这里改成 j=i 就可以统计到单个字符的情况
if (s.charAt(i) == s.charAt(j) && (j-i<=2 || dp[i+1][j-1])) {
dp[i][j]=true;
res++;
}
}
}
return res;
}
解法二
很熟悉的解法,没错就是我们之前 最长回文子串中 的解法,比上面的动态规划会快很多,也比较自然
//中心扩展法
public int countSubstrings(String s) {
if (s==null || s.length()<=0) {
return 0;
}
int n=s.length();
int count=0;
for (int i=0;i<n;i++) {
count+=spread(s,i,i+1)+spread(s,i,i);
}
return count;
}
public int spread(String s,int i,int j){
int res=0;
while(i>=0 && j<s.length()){
if (s.charAt(i)==s.charAt(j)) {
i--;j++;
res++;
}else{
return res;
}
}
return res;
}
32. 最长有效括号
给定一个只包含 ‘(’ 和 ‘)’ 的字符串,找出最长的包含有效括号的子串的长度。
示例 1:
输入:"(()"
输出:2
解释:最长有效括号子串为 "()"
示例 2:
输入:")()())"
输出:4
解释:最长有效括号子串为 "()()"
解法一
栈+dp 的思路
public int longestValidParentheses(String s) {
if (s==null || s.length()<=0) {
return 0;
}
Stack<Integer> stack=new Stack<>();
int[] dp=new int[s.length()]; //以 i 位置括号结尾的最长有效括号
dp[0]=0;
int res=0;
for (int i=0;i<s.length();i++) {
if (s.charAt(i)=='(') {
stack.push(i); //dp[i]=0
}else{
if(!stack.isEmpty()){
int left=stack.pop();
dp[i]= left==0?i-left+1:dp[left-1]+i-left+1;
res=Math.max(res,dp[i]);
}//else dp[i]=0
}
}
return res;
}
首先想到的就是这种解法,感觉还是很好理解的,栈中存索引,dp[i] 代表以i位置括号结尾的最长有效括号,当遇到右括号的时候将栈顶的左括号的索引left弹出来,两者形成的括号长度再加上左括号索引前一个元素dp[left-1]就是当前位置的dp[i]
Update
回头做第二遍地时候竟然写了个不一样的 dp 思路 hahaha~,还是挺有意思的,遇到右括号不是直接用i-left+1 算长度,而是直接根据前一个字符dp[i-1] 进行转化,其实是一样的,只不过是累加的,前面的是一次就全算出来了
//update: 2020.4.13
public int longestValidParentheses(String s) {
if(s==null || s.length()<=0) return 0;
Deque<Integer> stack=new ArrayDeque<>();
int[] dp=new int[s.length()];
int res=0;
for(int i=0;i<s.length();i++){
if(s.charAt(i)=='('){
stack.push(i);
}else{
if(!stack.isEmpty()){
int left=stack.pop();
//dp[i]=(left>1?dp[left-1]+dp[i-1]:dp[i-1])+2;
dp[i]=dp[i-1]+(left>1?dp[left-1]:0)+2;
}
res=Math.max(res,dp[i]);
}
}
return res;
}
解法二
纯 dp 解法,上面的解法虽然也用到了一点动态规划,但是还不够纯粹
public int longestValidParentheses(String s) {
if (s==null || s.length()<=0) {
return 0;
}
int[] dp=new int[s.length()];
dp[0]=0;
int res=0;
for (int i=1;i<s.length();i++) {
if (s.charAt(i)==')') {
if (s.charAt(i-1)=='(') { //前一个是左括号
dp[i]=i-2>=0?dp[i-2]+2:2;
}else{ //前一个是右括号 ()(())
if (i-dp[i-1]-1>=0 && s.charAt(i-dp[i-1]-1)=='(') {//前一个右括号的合法序列的前一个是'('
//前一个的前一个的 dp[i-dp[i-1]-2]+dp[i-1]+2
dp[i]=(i-dp[i-1]-2>=0?dp[i-dp[i-1]-2]:0)+dp[i-1]+2;
}
//前一个右括号的合法序列的前一个是')', 没救了
}
}
res=Math.max(res,dp[i]);
}
return res;
}
解释都在代码注释中,感觉没那么容易直接想到,毕竟 hard 题
Update: 2020.7.4
今天的打卡题,之前的做法只记得栈+dp 的做法,dp 的方法忘了,现场写了下纯 dp 的方法,发现其实纯 dp 的好像更简单啊,状态定义出来后,转移方程就呼之欲出了(是我变强了么🤣)
//和前面的写法不一样,感觉我的更好理解
func longestValidParentheses(s string) int {
var dp = make([]int, len(s)) //以 s[i] 结尾的最长有效括号
//dp[0] = 0
var res = 0
for i := 1; i < len(s); i++{
if s[i] == ')' {
if i - dp[i-1] - 1 >= 0 && s[i - dp[i-1] - 1] == '('{
dp[i] = dp[i - 1] + 2
if(i - dp[i-1] - 2 >= 0){
dp[i] += dp[i - dp[i-1] - 2]
}
}
}
res = Max(res, dp[i])
}
return res
}
func Max(a, b int) int{
if a > b{
return a
}
return b
}
其实还有两种方法,一种利用纯利用栈的,还有一种很神奇的方法,没什么通用性,很难直接想出来,就不做记录了,纯栈的解法后面再来补充
解法三
纯利用栈的解法以后再来补充 算了,直接写了吧
public int longestValidParentheses(String s) {
if (s==null || s.length()<=0) {
return 0;
}
Deque<Integer> stack=new ArrayDeque<>();
stack.push(-1); //临界点
int res=0;
for(int i=0;i<s.length();i++){
if(s.charAt(i)=='('){
stack.push(i);
}else{
stack.pop();
if(stack.isEmpty()){
//栈为空,说明当前的')'肯定是不合法的
//其实相当于一个分界点,这个位置之前的字符不可能再构成合法的序列了
//后面的栈空的时候就不能再根据-1 来算长度了,需要一个新的临界点
stack.push(i);
}else{
res=Math.max(res,i-stack.peek());
}
}
}
return res;
}
关键的地方就在于将非法的右括号入栈,作为一个分界点便于后面计算,初始的-1 也很关键
解法四
UPDATE: 2020.7.4,把之前所谓的“神奇”的方法也记录下,其实也没啥神奇的,看一下就懂了,这种方法还是很优秀的,空间复杂度为O(1)
//实时统计左右括号的个数,当匹配的时候统计长度,记得左右都要扫一遍
func longestValidParentheses(s string) int {
var left, right = 0, 0
var res = 0
for i := 0; i < len(s); i++ {
if s[i] == '(' {
left++
} else {
right++
}
if right > left {
right, left = 0, 0
}else if right == left {
res = Max(res, left*2)
}
}
right, left = 0, 0
for i := len(s) - 1; i >= 0; i-- {
if s[i] == '(' {
left++
} else {
right++
}
if right < left {
right, left = 0, 0
} else if right == left {
res = Max(res, left*2)
}
}
return res
}
func Max(a, b int) int {
if a > b {
return a
}
return b
}
面试题 17.13. 恢复空格
Difficulty: 中等
哦,不!你不小心把一个长篇文章中的空格、标点都删掉了,并且大写也弄成了小写。像句子"I reset the computer. It still didn’t boot!"已经变成了"iresetthecomputeritstilldidntboot"。在处理标点符号和大小写之前,你得先把它断成词语。当然了,你有一本厚厚的词典dictionary,不过,有些词没在词典里。假设文章用sentence表示,设计一个算法,把文章断开,要求未识别的字符最少,返回未识别的字符数。
注意: 本题相对原题稍作改动,只需返回未识别的字符数
示例:
输入:
dictionary = ["looked","just","like","her","brother"]
sentence = "jesslookedjustliketimherbrother"
输出: 7
解释: 断句后为"jess looked just like tim her brother",共 7 个未识别字符。
提示:
0 <= len(sentence) <= 1000dictionary中总字符数不超过 150000。- 你可以认为
dictionary和sentence中只包含小写字母。
解法一
同样的解法,用 Java 写就是 922ms,我觉得主要就是 substring 拖慢了速度,Java 里面 substring 是 O(N) 的操作,而 golang 中取切片值仅仅只是修改几个切片的熟悉罢了,时间复杂度是 O(1) 的,所以会很快,时间复杂度可以近似的看作 O(N^2)
//正向 dp,60ms
func respace(dictionary []string, sentence string) int {
var dict = make(map[string]bool)
for i := 0; i < len(dictionary); i++ {
dict[dictionary[i]] = true
}
var n = len(sentence)
//前 i 个字符的最少未识别字符
var dp = make([]int, n+1)
for i := 1; i <= n; i++ {
dp[i] = dp[i-1] + 1 //初始值
for j := 0; j < i; j++ {
if dict[sentence[j:i]] {
dp[i] = Min(dp[j], dp[i])
}
}
}
return dp[n]
}
func Min(a, b int) int {
if a < b {
return a
}
return b
}
查询了网上的一些资料,发现 Java 的 substring 其实在 1.7 之前时间复杂度是 O(1) 的,后面为了避免内存泄漏就改成 O(N) 了 参考
解法二
记忆化递归,其实一开始就被题目的 tag 给迷惑了,我一看记忆化,就直接往记忆化的方向去写了,加上前天刚写了 单词拆分 2 的记忆化,唉,看来以后不能直接看 tag 了,一开始写了个贼垃圾的 dfs,就是下面注释的部分,时间复杂度爆炸,两层 for 循环
//记忆化 dfs tle 了 可能思路有点问题
//确实是思路出了问题,下面补充了正确的记忆化写法 248ms
func respace(dictionary []string, sentence string) int {
var dict = make(map[string]bool)
for i := 0; i < len(dictionary); i++ {
dict[dictionary[i]] = true
}
var cache = make(map[string]int)
return dfs(sentence, dict, cache)
}
// func dfs(s string, dict map[string]bool, cache map[string]int) int {
// if _, ok := cache[s]; ok {
// return cache[s]
// }
// var res = len(s)
// for i := 0; i <= len(s); i++ {
// temp := len(s)
// for j := i + 1; j <= len(s); j++ {
// if dict[s[i:j]] {
// temp = Min(temp, dfs(s[j:], dict, cache))
// }
// }
// res = Min(res, temp+i)
// }
// cache[s] = res
// return res
// }
func dfs(s string, dict map[string]bool, cache map[string]int) int {
if _, ok := cache[s]; ok {
return cache[s]
}
var res = len(s)
for i := 1; i <= len(s); i++ {
if dict[s[:i]] {
res = Min(res, dfs(s[i:], dict, cache))
}else{
res = Min(res, dfs(s[i:], dict, cache) + i)
}
}
cache[s] = res
return res
}
func Min(a, b int) int {
if a < b {
return a
}
return b
}
解法三
上面的解法从某种角度上来说都还是是属于暴力解法,即使是 golang 的 O(N^2) 的方法,哈希表的常数也是很大的,而且因为是存的字符串,所以字符串本身 Hash 的时间也是不能忽略的,因此我们可以引入前缀树,不了解相关知识的可以看我 之前的文章
这里我用 golang 也写了一版,但是提升不明显,所以用 Java 重写了一版,时间复杂度有了质的飞跃
//Trie+dp 14ms, 很强
public int respace(String[] dictionary, String s) {
Node root = new Node();
for (String word : dictionary ) {
root.insert(word);
}
int n = s.length();
int[] dp = new int[n+1];
for (int i = 1; i <=n ; i++) {
dp[i] = dp[i-1] + 1;
Node cur = root;
for (int j = i-1; j >=0 ; j--) {
int c = s.charAt(j)-'a';
//很大的优化点,c 不存在,那么以 c 为后缀的其他字符肯定也不会存在,直接 break
if(cur.next[c] == null){
break;
}
if(cur.next[c].isWord){
dp[i] = Math.min(dp[i], dp[j]);
}
if(dp[i] == 0){
break;
}
cur = cur.next[c];
}
}
return dp[n];
}
//这里 Trie 不用写搜索,直接手动的搜索,这样可以做一些剪枝
class Node{
Node[] next = new Node[26];
boolean isWord;
//反向插入
public void insert(String s){
Node cur = this;
for (int i = s.length()-1; i >= 0; i--) {
int c = s.charAt(i)-'a';
if(cur.next[c] == null){
cur.next[c] = new Node();
}
cur = cur.next[c];
}
cur.isWord = true;
}
}
解法四
没错,这题解法很多,也都很值得学习,解法四其实就是之前学过的字符串哈希的方法,所以这个解法右转—>Rabin-Karp 算法
174. 地下城游戏
Difficulty: 困难
一些恶魔抓住了公主(P)并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士(K)最初被安置在左上角的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快到达公主,骑士决定每次只向右或向下移动一步。
编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。
例如,考虑到如下布局的地下城,如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下,则骑士的初始健康点数至少为 7。
| -2 (K) | -3 | 3 |
| -5 | -10 | 1 |
| 10 | 30 | -5 (P) |
说明:
-
骑士的健康点数没有上限。
-
任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
解法一
以后每日一题没写出来之前绝壁不看群了,看了一眼群,看见群友讨论了这题,说了二分和 dp,然后我就直接向二分的方向去想了,如果独立的想的话,应该也是可以得出二分的解法的,毕竟题目的描述很明显就是二分答案,最低的健康血量,大于这个血量的肯定可以救出来,小于这个血量的肯定救不出来,所以 check 就是判断在某个血量下,能否拯救到公主(DP)
时间复杂度 O(N^2logN)(其实我认为也可以当作 N^2 毕竟上下界都确定了,logN 也就 30 左右),这种解法也挺不错的,融合了二分和 dp
public int calculateMinimumHP(int[][] dungeon) {
int left = 0;
int right = Integer.MAX_VALUE;
int res = 0;
while(left <= right){
int mid = left + (right-left)/2;
if(check(dungeon, mid)){
res = mid;
right = mid - 1;
}else{
left = mid + 1;
}
}
return res;
}
public boolean check(int[][] dungeon, int live){
int m = dungeon.length;
int n = dungeon[0].length;
int INF = Integer.MIN_VALUE;
//live 的血量从左上到 dungeon[i][j] 的剩余最多血量
int[][] dp = new int[m+1][n+1];
//地牢外围加上 INF 的围墙,简化逻辑
Arrays.fill(dp[0], INF);
dp[0][1] = live;
for(int i = 1; i <= m; i++){
dp[i][0] = INF;
for(int j = 1; j <= n; j++){
if(dp[i-1][j] <= 0 && dp[i][j-1] <=0 ){
dp[i][j] = INF; //无法到达这里
}else{
dp[i][j] = dungeon[i-1][j-1] + Math.max(dp[i][j-1], dp[i-1][j]);
}
}
}
return dp[m][n] > 0;
}
当然这题也有纯 dp 的做法,很可惜,我压根没往上面想,我只想着二分 dp,写完了 AC 之后就去看评论区了,结果发现大家都是直接 dp 的。然后还看到了一个关键词:逆向 dp,然后赶紧关了评论区回来写了下面的 dp 解法
解法二
/*
-2 -3 3
-5 -10 1
10 30 -5 1
7 5 2
6 11 5
1 1 6
*/
public int calculateMinimumHP(int[][] dungeon) {
int m = dungeon.length;
int n = dungeon[0].length;
int INF = Integer.MAX_VALUE;
//从 dungeon[i-1][j-1] 到右下角至少要多少血量
int[][] dp = new int[m+1][n+1];
Arrays.fill(dp[m], INF);//末行
dp[m][n-1] = 1; //初始血量
for (int i = m-1; i >= 0; i--) {
dp[i][n] = INF; //首列和尾列
for (int j = n-1; j >= 0; j--) {
dp[i][j] = Math.max(Math.min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j], 1);
}
}
return dp[0][0];
}
这题为啥不能正向 dp 呢,设dp[i][j]为从左上角到 i,j 所需要的最低血量?其实这个很明显就是有问题的,没办法转移,dp[i][j]和dp[i-1][j]没有任何关系,都不一定是同一条路径
97. 交错字符串
Difficulty: 困难
给定三个字符串 s1, s2, s3, 验证 s3 是否是由 s1 和 s2 交错组成的。
示例 1:
输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
输出:true
示例 2:
输入:s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
输出:false
解法一
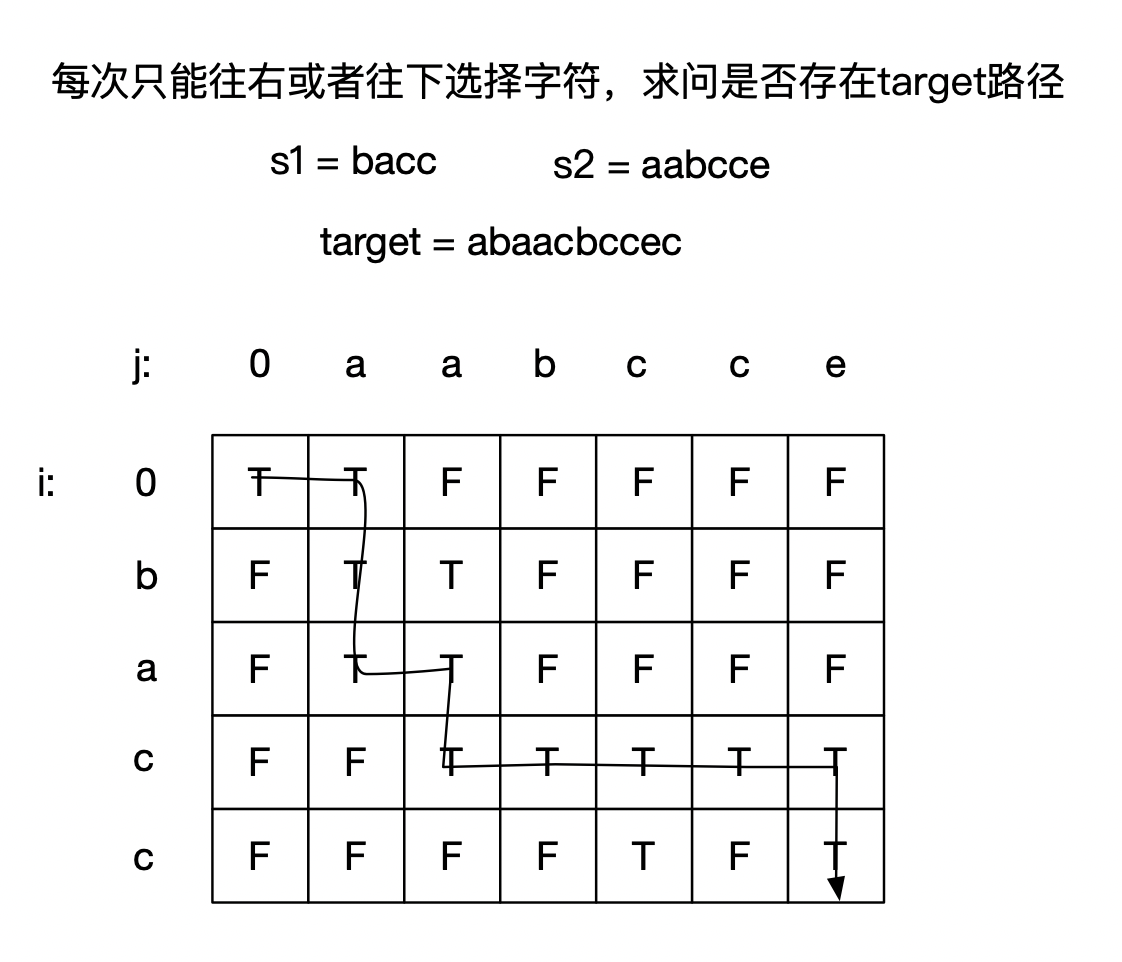
public boolean isInterleave(String s1, String s2, String s3) {
int ns1 = s1.length(), ns2 = s2.length(), ns3 = s3.length();
if(ns1+ns2!=ns3) return false;
boolean[][] dp = new boolean[ns1+1][ns2+1];
for(int i = 1; i <= ns1 && s1.charAt(i-1)==s3.charAt(i-1); i++){
dp[i][0] = true;
}
for(int i = 1; i <= ns2 && s2.charAt(i-1)==s3.charAt(i-1); i++){
dp[0][i] = true;
}
dp[0][0] = true;
for(int i = 1; i <= ns1; i++){
for(int j = 1; j <= ns2; j++){
char sc = s3.charAt(i+j-1);
dp[i][j] = (sc == s1.charAt(i-1) && dp[i-1][j])
|| sc == s2.charAt(j-1) && dp[i][j-1];
}
}
return dp[ns1][ns2];
}
857. 最小的窗口子序列(LintCode)
给定字符串 S 和 T,在字符串 S 中找到最小(连续的)子字符串 W(窗口),使得 T 是 W 的子序列。 如果 S 中没有包含 T 中的所有字符的窗口,则返回空字符串""。如果有多个这样的最小长度窗口,则返回一个起点编号最小的。
- 输入中的所有字符串只包含小写字母。
- S 的长度范围在 [1, 20000]。
- T 的长度范围在 [1, 100]。
样例 1:
输入:S="jmeqksfrsdcmsiwvaovztaqenprpvnbstl",T="u"
输出:""
解释: 无法匹配
样例 2:
输入:S = "abcdebdde", T = "bde"
输出:"bcde"
解释:"bcde"是答案,"deb"不是一个较小的窗口,因为窗口中的 T 元素必须按顺序发生。
解法一
LeetCode 上是会员题,所以在 LintCode 上写的,一开始以为是滑窗,想了半天,也只有暴力的思路,看了下讨论区,发现大家都是 dp 做的。
public String minWindow(String S, String T) {
int m = S.length(), n = T.length();
//S 前 i 个字符包含 T 前 j 个字符的最小窗口子序列起始位置
int[][] dp = new int[m+1][n+1];
for (int i = 0; i <= m; i++){
//虽然 T 串为空,但是注意这里不是 0,因为需要最短,所以起点越靠后越短
//最后的长度就是通过 i-dp[i][j] 来计算的
Arrays.fill(dp[i], -1);
dp[i][0] = i;
}
int start = -1, end = m;
for (int i = 1; i <= m; i++) {
//注意 T 的长度小于 S 的长度(不考虑也可以,只是会多遍历很多次)
for (int j = 1; j <= Math.min(n, i); j++){
if (S.charAt(i-1) == T.charAt(j-1)) {
dp[i][j] = dp[i-1][j-1];
}else{
//dbd
// b dbd 和 db 包含 b 的最小窗口起始位置一样
dp[i][j] = dp[i-1][j];
}
}
if (dp[i][n]!=-1 && i-dp[i][n] < end-start+1) {
start = dp[i][n];
end = i-1;
}
}
return start==-1 ? "" : S.substring(start,end+1);
}
这题和滑动窗口专题中的 最小覆盖子串 算是一道姊妹题,但是解法确完全不一样,当然这题也可以滑窗但是并不是很通用(主要是我没看懂)貌似会比 dp 要好
双序列型 DP,后面有时间会把类似的题单独抽取出来
1553. 吃掉 N 个橘子的最少天数
Difficulty: 困难
厨房里总共有 n 个橘子,你决定每一天选择如下方式之一吃这些橘子:
- 吃掉一个橘子。
- 如果剩余橘子数
n能被 2 整除,那么你可以吃掉n/2个橘子。 - 如果剩余橘子数
n能被 3 整除,那么你可以吃掉2*(n/3)个橘子。
每天你只能从以上 3 种方案中选择一种方案。
请你返回吃掉所有 n 个橘子的最少天数。
示例 1:
输入:n = 10
输出:4
解释:你总共有 10 个橘子。
第 1 天:吃 1 个橘子,剩余橘子数 10 - 1 = 9。
第 2 天:吃 6 个橘子,剩余橘子数 9 - 2*(9/3) = 9 - 6 = 3。(9 可以被 3 整除)
第 3 天:吃 2 个橘子,剩余橘子数 3 - 2*(3/3) = 3 - 2 = 1。
第 4 天:吃掉最后 1 个橘子,剩余橘子数 1 - 1 = 0。
你需要至少 4 天吃掉 10 个橘子。
示例 2:
输入:n = 6
输出:3
解释:你总共有 6 个橘子。
第 1 天:吃 3 个橘子,剩余橘子数 6 - 6/2 = 6 - 3 = 3。(6 可以被 2 整除)
第 2 天:吃 2 个橘子,剩余橘子数 3 - 2*(3/3) = 3 - 2 = 1。(3 可以被 3 整除)
第 3 天:吃掉剩余 1 个橘子,剩余橘子数 1 - 1 = 0。
你至少需要 3 天吃掉 6 个橘子。
示例 3:
输入:n = 1
输出:1
示例 4:
输入:n = 56
输出:6
提示:
1 <= n <= 2*10^9
解法一
题目很简单,暴力的方法非常容易想到,但是问题是这题的数据范围比较大2*1e9,直接暴搜肯定会 T,所以需要优化下,这里我们可以直接将minDays(n-1)优化掉,将这种只吃一个的情况和其他情况和并,比如我现在 n=5,那么我们就可以直接求Min(minDays(2)+1, minDays(1)+2),5 没法被 2 或者 3 整除,所以我们将 5 吃掉几个,变成可以被 2 和 3 整除的,吃掉的个数就是 n%2 和 n%3,也就是在这之前额外需要的天数
var dp = make(map[int]int)
func minDays(n int) int {
if n == 1 || n == 0 {
return n
}
if v, ok := dp[n]; ok {
return v
}
res := 1+Min(minDays(n/2)+n%2, minDays(n/3)+n%3)
dp[n] = res
return res
}
func Min (a, b int) int {
if a < b {
return a
}
return b
}
NC549. 变向
牛牛准备在一个 3 行 n 列的跑道上跑步。一开始牛牛可以自己选择位于 (1,1) 还是 (2,1) 还是 (3,1)。
跑道的每一格都有一些金币,当牛牛跑到一个格子,他会获得这个格子的所有金币。
当牛牛位于第 i 行第 j 列时,他可以的下一步最多可能有三种选择:
- 不花费金币跑到第 i 行第 j+1 列
- 花费
m[j]的金币跑到第 i-1 行第 j+1 列(如果 i=1 则不可以这么跑)。 - 花费
m[j]的金币跑到第 i+1 行第 j+1 列(如果 i=3 则不可以这么跑)。 (牛牛是一个富豪,本身带了很多的金币,所以你不用担心他钱不够用) 现在告诉你所有格子的金币数量和每一列的金币花费,牛牛想知道他跑到第 n 列最多可以赚得多少金币(赚得金币=获得金币-消耗金币)
示例 1
输入:3,[1,9,3],[6,4,6],[1,1,5],[3,2,1]
输出:16
说明:一开始牛牛选择位于第 2 行第 1 列,拿到 6 个金币。然后牛牛花 3 金币到第 1 行的 2 列拿到 9 个金币,最后牛牛花费 2 金币到第 2 行第 3 列。总共获得 21 金币,消耗 5 金币。赚得 16 金币。
备注:
-
2 <= n <= 1e5
-
第 1 个参数 n 代表跑道的列数 第 2,3,4 个参数 vector
a1,a2,a3 各有 n 个元素,代表第 1,2,3 行每一列的金币个数 第 5 个参数 vector m 有 n 个元素代表每一列进行换行的时候需要的金币花费
解法一
题目意思搞清楚就行了
//很直白的 dp
public int solve (int n, int[] a1, int[] a2, int[] a3, int[] m) {
// write code here
int[][] dp = new int[3][n];
dp[0][0] = a1[0];
dp[1][0] = a2[0];
dp[2][0] = a3[0];
for (int j = 1; j < n; j++) {
dp[0][j] = a1[j] + Math.max(dp[0][j-1], dp[1][j-1]-m[j-1]);
dp[1][j] = a2[j] + Math.max(dp[1][j-1], Math.max(dp[0][j-1]-m[j-1], dp[2][j-1]-m[j-1]));
dp[2][j] = a3[j] + Math.max(dp[2][j-1], dp[1][j-1]-m[j-1]);
}
return Math.max(dp[0][n-1],Math.max(dp[1][n-1], dp[2][n-1]));
}
NC554 简单变向
牛牛准备在一个 3 行 n 列的跑道上跑步。一开始牛牛位于 (1,1)。
当牛牛位于第 i 行第 j 列时,他可以的下一步最多可能有三种选择:
- 跑到第 i 行第 j+1 列
- 跑到第 i-1 行第 j+1 列(如果 i=1 则不可以这么跑)。
- 跑到第 i+1 行第 j+1 列(如果 i=3 则不可以这么跑)。
跑道上有一些格子设置了路障(一个格子可能有多个路障),牛牛不能跑到路障上。现在牛牛想知道,从 (1,1) 到 (3,n) 有多少条不同的路径?
为了防止答案过大,答案对 1e9+7 取模。
比较简单就不贴 case 了
解法一
注意溢出就行了
public int solve (int n, int m, int[] x, int[] y) {
long[][] dp = new long[3][n+1];
int MOD = (int)1e9+7;
boolean[][] v = new boolean[3][n];
for(int i = 0; i < m; i++){
v[x[i]-1][y[i]-1] = true;
}
dp[0][0] = 1;
for (int j = 1; j < n; j++) {
dp[0][j] = v[0][j] ? 0 : (dp[0][j-1] + dp[1][j-1])%MOD;
dp[1][j] = v[1][j] ? 0 : (dp[1][j-1] + dp[0][j-1]+dp[2][j-1])%MOD;
dp[2][j] = v[2][j] ? 0 : (dp[2][j-1] + dp[1][j-1])%MOD;
}
return (int)(dp[2][n-1]%MOD);
}
787. K 站中转内最便宜的航班
Difficulty: 中等
有 n 个城市通过 m 个航班连接。每个航班都从城市 u 开始,以价格 w 抵达 v。
现在给定所有的城市和航班,以及出发城市 src 和目的地 dst,你的任务是找到从 src 到 dst 最多经过 k 站中转的最便宜的价格。 如果没有这样的路线,则输出 -1。
示例 1:
输入:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
输出:200
解释:
城市航班图如下
从城市 0 到城市 2 在 1 站中转以内的最便宜价格是 200,如图中红色所示。
示例 2:
输入:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
输出:500
解释:
城市航班图如下
从城市 0 到城市 2 在 0 站中转以内的最便宜价格是 500,如图中蓝色所示。
提示:
n范围是[1, 100],城市标签从0到n- 1.- 航班数量范围是
[0, n * (n - 1) / 2]. - 每个航班的格式
(src,dst``, price). - 每个航班的价格范围是
[1, 10000]. k范围是[0, n - 1].- 航班没有重复,且不存在环路
解法一
范围很小只有 100,一开始以为是 Floyd,但是有 K 的限制不好处理
func findCheapestPrice(n int, flights [][]int, src int, dst int, K int) int {
//dp[i][k]:从 src 到 i 节点中转 k 次最短距离
var Min = func(a, b int) int {if a<b {return a};return b}
var INF = 0x3f3f3f3f
var dp = make([][]int, n)
for i := 0; i < n; i++ {
//K+2 是为了方便初始化,不用单独处理 K==0 的情况
dp[i] = make([]int, K+2)
for j := 0; j <= K+1; j++ {
dp[i][j] = INF
}
}
for k := 0; k <= K+1; k++ {
dp[src][k] = 0
}
for k := 1; k <= K+1; k++ {
for _,flt := range flights {
//src 到 flt[1] 通过 flt[0] 中转
dp[flt[1]][k] = Min(dp[flt[1]][k], dp[flt[0]][k-1]+flt[2])
}
}
if dp[dst][K+1] == INF {
return -1
}
return dp[dst][K+1]
}
这题也可以
Dijkstra但是我不会
NC557. 好多牛牛
给出一个字符串 S,牛牛想知道这个字符串有多少个子序列等于"niuniu"子序列可以通过在原串上删除任意个字符(包括 0 个字符和全部字符)得到。为了防止答案过大,答案对 1e9+7 取模
示例 1
输入:"niuniniu"
输出:3
说明:
删除第 4,5 个字符可以得到"niuniu"
删除第 5,6 个字符可以得到"niuniu"
删除第 6,7 个字符可以得到"niuniu"
备注: 10 <= len(s) <= 1e5
解法一
菜啊,没想出来,真的菜
//UPDATE: 2020.9.27,之前的解法过了 OJ,但是其实是有问题的
//二维 DP(不方便优化成一维的)
public int solve1 (String s) {
// write code here
String p = "niuniu";
int m = p.length();
int n = s.length();
int MOD = (int)1e9+7;
//dp[i][j] 代表 s[0,j] 中有多少个 p[0,j]
long[][] dp = new long[7][n+1];
Arrays.fill(dp[0], 1);
for (int i = 1; i <= m; i++){
for (int j = 1; j <= n; j++){
if (s.charAt(j-1) == p.charAt(i-1)) {
//dp[i][j] = (dp[i-1][j] + dp[i][j-1]) % MOD;
//上面的是错的,之所以正确是因为题目的 niuniu 没有连续的相同字符
//考虑如下 case: p = "aa" , s = "abaa" wa = 6, ac = 3
dp[i][j] = (dp[i-1][j-1] + dp[i][j-1]) % MOD;
} else {
dp[i][j] = dp[i][j-1];
}
}
}
return (int)dp[m][n];
}
实际上这个解法最好把内外循环交换下,这样更好降维
//二维 DP,交换内外循环
public int solve2 (String s) {
// write code here
String p = "niuniu";
int n = s.length();
int m = p.length();
int MOD = (int)1e9+7;
//dp[i][j] 代表 s[0,i] 中有多少个 p[0,j]
long[][] dp = new long[n+1][m+1];
dp[0][0] = 1;
for (int i = 1; i <= n; i++){
dp[i][0] = 1;
for (int j = 1; j <= m; j++){
if (s.charAt(i-1) == p.charAt(j-1)) {
dp[i][j] = (dp[i-1][j-1] + dp[i-1][j]) % MOD;
} else {
dp[i][j] = dp[i-1][j];
}
}
}
return (int)dp[n][m];
}
解法二
按照上面交换内外循环后的解法再降维
//UPDATE: 2020.9.27,之前的解法过了 OJ,但是其实是有问题的
//按上面的来降维舒服多了
public int solve3 (String s) {
String p = "niuniu";
int n = s.length();
int m = p.length();
int MOD = (int)1e9+7;
//dp[j] 代表 s[0,i] 中有多少个 p[0,i]
long[] dp = new long[m+1];
dp[0] = 1;
for (int i = 1; i <= n; i++){
//for (int j = 1; j <= m; j++){
//内层应该反过来递推,保证 dp[j] 和 dp[j-1] 是上一次的
for (int j = m; j >= 1; j--){
if (s.charAt(i-1) == p.charAt(j-1)) {
dp[j] = (dp[j] + dp[j-1]) % MOD;
}
}
}
return (int)dp[m];
}
926. 将字符串翻转到单调递增
Difficulty: 中等
如果一个由 '0' 和 '1' 组成的字符串,是以一些 '0'(可能没有 '0')后面跟着一些 '1'(也可能没有 '1')的形式组成的,那么该字符串是_单调递增_的。
我们给出一个由字符 '0' 和 '1' 组成的字符串 S,我们可以将任何 '0' 翻转为 '1' 或者将 '1' 翻转为 '0'。
返回使 S 单调递增的最小翻转次数。
示例 1:
输入:"00110"
输出:1
解释:我们翻转最后一位得到 00111.
示例 2:
输入:"010110"
输出:2
解释:我们翻转得到 011111,或者是 000111。
示例 3:
输入:"00011000"
输出:2
解释:我们翻转得到 00000000。
提示:
1 <= S.length <= 20000S中只包含字符'0'和'1'
解法一
动态规划的解法
func minFlipsMonoIncr(S string) int {
var n = len(S)
//dp[i][0]: [0~i] s[i]==0 需要最小额翻转次数
//dp[i][1]: [0~i] s[i]==1 需要最小额翻转次数
var dp = make([][2]int, n)
var Min = func(a, b int) int {if a < b {return a}; return b}
var preSum = make([]int, n+1)
for i := 1; i <= n; i++ {
preSum[i] = preSum[i-1] + int(S[i-1]-48)
}
if S[0] == '1' {
dp[0][0] = 1
}else {
dp[0][1] = 1
}
for i := 1; i < n; i++ {
if S[i] == '1' {
dp[i][1] = Min(dp[i-1][1], dp[i-1][0])
dp[i][0] = preSum[i+1] //包含 i
} else {
dp[i][0] = preSum[i] //不包含 i
dp[i][1] = Min(dp[i-1][0], dp[i-1][1]) + 1
}
}
return Min(dp[n-1][1], dp[n-1][0])
}
解法二
寻找分割点,使得分割点左边的 1 和右边的 0 相加的和最少
//Trick,寻找分割点,使得分割点左边的 1 和右边的 0 相加的和最少
func minFlipsMonoIncr(S string) int {
var count0 = 0 //分割点右边的 0
var count1 = 0 //分割点左边的 1
var Min = func(a, b int) int {if a < b {return a}; return b}
for i := 0; i < len(S); i++ {
if S[i] == '0' {
count0++
}
}
var res = count0
for i := 0; i < len(S); i++ {
if S[i] == '1' {
count1++
} else {
count0--
}
res = Min(res, count1+count0)
}
return res
}
LCP 19. 秋叶收藏集
小扣出去秋游,途中收集了一些红叶和黄叶,他利用这些叶子初步整理了一份秋叶收藏集 leaves, 字符串 leaves 仅包含小写字符 r 和 y, 其中字符 r 表示一片红叶,字符 y 表示一片黄叶。 出于美观整齐的考虑,小扣想要将收藏集中树叶的排列调整成「红、黄、红」三部分。每部分树叶数量可以不相等,但均需大于等于 1。每次调整操作,小扣可以将一片红叶替换成黄叶或者将一片黄叶替换成红叶。请问小扣最少需要多少次调整操作才能将秋叶收藏集调整完毕。
示例 1:
输入:leaves = "rrryyyrryyyrr"
输出:2
解释:调整两次,将中间的两片红叶替换成黄叶,得到 "rrryyyyyyyyrr"
示例 2:
输入:leaves = "ryr"
输出:0
解释:已符合要求,不需要额外操作
提示:
3 <= leaves.length <= 10^5
leaves 中只包含字符 'r' 和字符 'y'
解法一
和上一题 926. 将字符串翻转到单调递增一样,不过很明显这里有三个状态,一个是前面的 r 结尾,一个是中间的 y 结尾,一个是末尾的 r 结尾,最后求出以最后的 r 结尾的最短次数就 ok 了
public int minimumOperations(String s) {
int n = s.length();
int[][] dp = new int[n+1][3];
//0,1,2 分别代表 前面的 r 中间的 y 结尾的 r
dp[0][0] = s.charAt(0) == 'r' ? 0 : 1;
dp[0][1] = dp[0][2] = dp[1][2] = 0x3f3f3f3f;
//简单的递推
for (int i = 1; i < n; i++) {
if (s.charAt(i) == 'r') {
dp[i][0] = dp[i-1][0];
dp[i][1] = Math.min(dp[i-1][1]+1, dp[i-1][0]+1);
dp[i][2] = Math.min(dp[i-1][2], dp[i-1][1]);
} else {
dp[i][0] = dp[i-1][0]+1;
dp[i][1] = Math.min(dp[i-1][0], dp[i-1][1]);
dp[i][2] = Math.min(dp[i-1][2]+1, dp[i-1][1]+1);
}
}
return dp[n-1][2];
}
空间还可以优化,代码也还可以更简洁,不过我懒得改了
845. 数组中的最长山脉
Difficulty: 中等
我们把数组 A 中符合下列属性的任意连续子数组 B 称为 “山脉”:
B.length >= 3- 存在
0 < i < B.length - 1使得B[0] < B[1] < ... B[i-1] < B[i] > B[i+1] > ... > B[B.length - 1]
(注意:B 可以是 A 的任意子数组,包括整个数组 A。)
给出一个整数数组 A,返回最长 “山脉” 的长度。
如果不含有 “_山脉” _则返回 0。
示例 1:
输入:[2,1,4,7,3,2,5]
输出:5
解释:最长的 “山脉” 是 [1,4,7,3,2],长度为 5。
示例 2:
输入:[2,2,2]
输出:0
解释:不含 “山脉”。
提示:
0 <= A.length <= 100000 <= A[i] <= 10000
示例 1:
输入:[2,1,4,7,3,2,5]
输出:5
解释:最长的山脉是 [1,4,7,3,2],长度为 5。
示例 2:
输入:[2,2,2]
输出:0
解释:不含山脉
解法一
遍历的过程中记录上升和下降的长度,然后注意重置的时机,当且仅当 up 和 down 都大于 0 的时候为合法,统计一个最大值就可以了
public int longestMountain(int[] A) {
int res = 0;
int up = 0, down = 0;
//[2,1,4,7,3,2,5]
for (int i = 1; i < A.length; i++) {
//前面是下降,这里开始增加或者和前一个元素相同,需要重置
if ((down > 0 && A[i] > A[i-1]) || A[i] == A[i-1]) {
up = down = 0;
}
up += A[i] > A[i-1] ? 1 : 0;
down += A[i] < A[i-1] ? 1 : 0;
if (up > 0 && down > 0) {
res = Math.max(res, up+down+1);
}
}
return res;
}
区间 DP
后面有时间会单独将这些题目分类整理成文章,目前暂时先这样
312. 戳气球
有 n 个气球,编号为 0 到 n-1,每个气球上都标有一个数字,这些数字存在数组 nums 中。
现在要求你戳破所有的气球。每当你戳破一个气球 i 时,你可以获得 nums[left] * nums[i] * nums[right] 个硬币。 这里的 left 和 right 代表和 i 相邻的两个气球的序号。注意当你戳破了气球 i 后,气球 left 和气球 right 就变成了相邻的气球。
求所能获得硬币的最大数量。
说明:
- 你可以假设 nums[-1] = nums[n] = 1,但注意它们不是真实存在的所以并不能被戳破。
- 0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100
示例:
输入:[3,1,5,8]
输出:167
解释:nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167
解法一
暴力回溯,其实就是尝试所有的组合,这样时间复杂度O(N!) ,数据超过十几就不行了
public int maxCoinsTLE(int[] nums) {
LinkedList<Integer> list=new LinkedList<>();
for (int n:nums) list.add(n);
dfs(list,0);
return max;
}
private int max=0;
public void dfs(LinkedList<Integer> list,int sum) {
if (list.size()==0) {
max=Math.max(sum,max);
return;
}
for (int i=0;i<list.size();i++) {
int temp=list.get(i);
//这个值要先算
int cur=(i-1<0?1:list.get(i-1))*(i+1>=list.size()?1:list.get(i+1))*temp;
list.remove(i);
dfs(list,sum+cur);
list.add(i,temp);
}
}
解法二
区间型动态规划,也是我第一次听说这个名词,但是之前其实已经做了不少的区间型的 dp 了
public int maxCoins(int[] nums) {
if (nums==null || nums.length<=0) {
return 0;
}
int[] A=new int[nums.length+2];
A[0]=1;A[A.length-1]=1;
for (int i=0;i<nums.length;i++) {
A[i+1]=nums[i]; //copy 一个新数组
}
//区间 DP
int n=A.length;
int[][] dp=new int[n][n]; //dp[i][j] 代表的是不包含边界 i,j 的最大得分
for (int len=2;len<=n;len++) { //枚举区间长度
for (int i=0;i<=n-len;i++) { //枚举起点
int j=i+len-1; //区间终点
for (int k=i+1;k<j;k++) { //枚举分割点
dp[i][j]=Math.max(dp[i][j],dp[i][k]+dp[k][j]+A[k]*A[i]*A[j]);
}
}
}
return dp[0][n-1];
}
这里为了处理边界将数组头尾插入了 1,copy 了一个新的数组,下面的区间型 dp 也是在看了题解,然后对着板子写的,当然这题的关键不是这里,关键是如何规划,这里搬运 题解区大佬 的解释
我们来分析一下按照上面的那个递归的思路状态转移方程能写吗?如果按照上面的递归的思路,我们定义 dp[i][j] 表示对于 i-j 的气球的最大的收益,那状态转移方程就是
dp[i][j]=max(coins[k]* coins[k-1] * coins[k+1]+dp[i][k-1]+dp[k+1][j]) k∈[i,j],
就按上面的那个例子,[3,1,5,8], 来写一下过程
扎爆 3 剩下 [] 和 [1,5,8]
扎爆 1 剩下 [3] 和 [5,8]
扎爆 5 剩下 [3,1] 和 [8]
扎爆 8 剩下 [3,1,5] 和 []
然后在这些里面找到一个最大值返回,这其中对于扎爆 1 和 8 的最大的收益这样定义是没有问题的,因为两者都在边界,但是对于扎爆 1 和 5 就有问题了,就拿先扎爆 1 来说,扎爆 1,剩下的最大的收益变为了 [3] 和 [5,8] 这两个区间的最大的收益的和,这个肯定不对,因为剩下的 [3,5,8] 区间的最大的收益的和不会是 [3] 的最大收益和与 [5,8] 的最大收益和的总和构成的,所以这个状态转移方程是不对的
那应该怎么定义状态转移方程呢,这也就是这道题巧妙的地方,它使用逆向思维,也就是上面的状态转移方程是由某个气球先爆得出来的,那么这里我们让指定的气球最后爆,这样的话状态转移方程为
dp[i][j]=max(coins[k]*coins[i-1]*coins[j+1]+dp[i][k-1]+dp[k+1][j]) k∈[i,j]
再来看上面的例子,就对了,也就是对于 [i,j] 的气球,我们让某个位置的气球最后再爆,求出它左区间的最大的收益和右区间的最大的收益,加上这个气球最后爆掉所获得的收益,一 一比较,返回一个最大值就好了,这里要注意的是,要按区间的长度来进行状态的转移,也就是先求长度为 1 的,然后 2 的依次类推,因为这里状态转移方程涉及到了当前位置的后面的区间的最大的收益,但是后面的区间的长度是小于当前区间的长度的,故应该按长度来进行状态的转移,这也是典型的区间型动态规划的套路
解法三
在解法二的基础上简化了代码,dp[i][j]代表i和j之间,包含i和j位置,戳爆所有气球的最大得分
public int maxCoins(int[] nums) {
if (nums==null || nums.length<=0) {
return 0;
}
int n=nums.length;
//dp[i][j] 代表的是包含边界 i,j 的最大得分
int[][] dp=new int[n][n];
for (int len=1;len<=n;len++) { //枚举区间长度
for (int i=0;i<=n-len;i++) { //枚举起点
int j=i+len-1; //区间终点
for (int k=i;k<=j;k++) { //枚举分割点
dp[i][j]=Math.max(dp[i][j],(k-1>=0?dp[i][k-1]:0)+(k+1<n?dp[k+1][j]:0)+nums[k]*(i-1>=0?nums[i-1]:1)*(j+1<n?nums[j+1]:1));
}
}
}
return dp[0][n-1];
}
UPDATE:2020.7.19 打卡题,重新写一遍,稍微好一点的写法,上面一堆三目不太好
func maxCoins(nums []int) int {
if len(nums) <= 0{
return 0
}
nums = append(nums, 1)
nums = append([]int{1}, nums...)
var n = len(nums)
var dp = make([][]int, n)
for i := 0; i < n; i++{
dp[i] = make([]int, n)
}
for tlen := 1; tlen <= n-2; tlen++{ //枚举区间长度
for left := 1; left+tlen-1 < n-1; left++{ //枚举左端点
right := left+tlen-1 //右端点
for k := left; k <= right; k++{ //枚举分割点
dp[left][right] = Max(dp[left][right], dp[left][k-1]+dp[k+1][right]+nums[k]*nums[left-1]*nums[right+1])
}
}
}
return dp[1][n-2]
}
func Max(a, b int)int{
if a > b{
return a
}
return b
}
877. 石子游戏
亚历克斯和李用几堆石子在做游戏。偶数堆石子排成一行,每堆都有正整数颗石子 piles[i] 。
游戏以谁手中的石子最多来决出胜负。石子的总数是奇数,所以没有平局。
亚历克斯和李轮流进行,亚历克斯先开始。 每回合,玩家从行的开始或结束处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止,此时手中石子最多的玩家获胜。
假设亚历克斯和李都发挥出最佳水平,当亚历克斯赢得比赛时返回 true ,当李赢得比赛时返回 false 。
示例:
输入:[5,3,4,5]
输出:true
解释:
亚历克斯先开始,只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗,这一行就变成了 [3,4,5] 。
如果李拿走前 3 颗,那么剩下的是 [4,5],亚历克斯拿走后 5 颗赢得 10 分。
如果李拿走后 5 颗,那么剩下的是 [3,4],亚历克斯拿走后 4 颗赢得 9 分。
这表明,取前 5 颗石子对亚历克斯来说是一个胜利的举动,所以我们返回 true 。
提示:
2 <= piles.length <= 500piles.length是偶数。1 <= piles[i] <= 500sum(piles)是奇数。
解法一
博弈型 dp,先采用区间 dp 的解法试试(区间 dp 是真的妙啊!!!)
//通用的区间 DP
public boolean stoneGame(int[] piles) {
//[5,3,4,5]
int N=piles.length;
//(i~j) 先手 (0), 后手 (1) 的最大收益
int[][][] dp=new int[N][N][2];
//base init len=1 的情况
for(int i=0;i<N;i++){
dp[i][i][0]=piles[i];
dp[i][i][1]=0;
}
for (int len=2;len<=N;len++) { //枚举区间长度
for (int left=0;left<=N-len;left++) { //枚举所有区间
//left+len-1<N
int right=left+len-1;
//先手拿 left 或者 right 的最大收益
//我先手拿了 left 或者 right 之后,剩下 [left+1,right] 或 [left,right-1] 区间
//我在剩下的区间中继续选其实就成为了后手,所以我们加上剩下区间的后手最大值
int firLeft=piles[left]+dp[left+1][right][1];
int firRight=piles[right]+dp[left][right-1][1];
if(firLeft>firRight){
dp[left][right][0]=firLeft;
//先手选 left 那么就相当于让另一个人(后手)从 [left+1,right] 中先手取最大值
dp[left][right][1]=dp[left+1][right][0];
}else{
dp[left][right][0]=firRight;
//同上
dp[left][right][1]=dp[left][right-1][0];
}
}
}
return dp[0][N-1][0]-dp[0][N-1][1]>0;
}
解法二
数学推理的方法,具体的证明给不出来,但是很容易理解它的正确性
//数学
public boolean stoneGame(int[] piles) {
return true;
}
首先题目有两个特殊的条件(这两个条件我解法一没用到)piles.length 是偶数,sum(piles) 是奇数,这其实说明了不会有平局,因为是偶数,我们把所有的柱子用奇偶来划分,那么奇数柱子和偶数石头堆的数量一定是相同的,而且两者总的石头数一定有一个数量的差异,不可能相等,我先手拿的话我就可以只考虑拿较大的那一类石头堆,那我能保证我拿到的一定是奇数或偶数的堆吗?其实随便举一个例子就知道了,比如 4 堆石头,先手的人总是能控制自己一定拿到 1,3 或者 2,4 所以先手的一定是可以赢得,推广到 N 堆石头也同样适用
1039. 多边形三角剖分的最低得分
给定 N,想象一个凸 N 边多边形,其顶点按顺时针顺序依次标记为 A[0], A[i], ..., A[N-1]。
假设您将多边形剖分为 N-2 个三角形。对于每个三角形,该三角形的值是顶点标记的乘积,三角剖分的分数是进行三角剖分后所有 N-2 个三角形的值之和。
返回多边形进行三角剖分后可以得到的最低分。
示例 1:
输入:[1,2,3]
输出:6
解释:多边形已经三角化,唯一三角形的分数为 6。
实例 2:
输入:[3,7,4,5]
输出:144
解释:有两种三角剖分,可能得分分别为:3*7*5 + 4*5*7 = 245,或 3*4*5 + 3*4*7 = 144。最低分数为 144。
解法一
区间 DP 套路,枚举所有的区间和区间内的点,区间内的点和区间左右端点将整个区间又划分为两个已知的子区间,典型的区间 dp
//环形的结构
public int minScoreTriangulation(int[] A) {
if(A==null || A.length<=0) return 0;
int N=A.length;
//从 0 ~ N-1 形成一个环
// 1-3
// / \
// 5 1
// \ /
// 1—4
// dp[left][right] 代表 left~right 区间形成的环的最小得分值
int[][] dp=new int[N][N];
for (int len=3;len<=N;len++) { //枚举长度,从 3 开始
for (int left=0;left<=N-len;left++) { //枚举左端点
//left+len-1<N
int right=left+len-1;
//init 初始化区间值
dp[left][right]=Integer.MAX_VALUE;
for (int i=left+1;i<right;i++) { //枚举区间内的所有的点(不包括端点)), 将环分割成左右两部分
dp[left][right]=Math.min(dp[left][right],dp[left][i]+dp[i][right]+A[i]*A[left]*A[right]);
}
}
}
return dp[0][N-1];
}
516. 最长回文子序列
给定一个字符串 s,找到其中最长的回文子序列。可以假设 s 的最大长度为 1000。
示例 1:
输入:
"bbbab"
输出:
4
一个可能的最长回文子序列为 "bbbb"。
示例 2:
输入:
"cbbd"
输出:
2
一个可能的最长回文子序列为 "bb"。
解法一
动态规划,dp[i][j] 代表 i~j 的最长回文串
public int longestPalindromeSubseq(String s) {
if (s==null || s.length()<=0) {
return 0;
}
int n=s.length();
int[][] dp=new int[n][n]; //dp[i][j] 代表 i~j 的最长回文子串
for (int i=0;i<n;i++) {
dp[i][i]=1;
}
//bbbab
for (int i=n-1;i>=0;i--) {
for (int j=i+1;j<n;j++) {
if (s.charAt(i)==s.charAt(j)) {
dp[i][j]=dp[i+1][j-1]+2;
}else{
dp[i][j]=Math.max(dp[i+1][j],dp[i][j-1]);
}
}
}
return dp[0][n-1];
}
核心的 dp 公式:
s[i]==p[j],dp[i][j]=dp[i+1][j-1]+2s[i]!=p[j],dp[i][j]=max(dp[i+1][j],dp[i][j-1])
是不是有的眼熟?没错,和 LCS 的 dp 思路很相似
这里其实还有个需要注意的地方,就是两次循环的方向,我们要保证每次计算 dp 值的时候右值都是已经计算过的,所以需要调整循环的执行方向让 i从右往左,让j从i向右,这样 i+1 和 j-1 的 dp 就都是计算过的了
UPDATE
//update: 2020.4.19
//区间 dp 写法,更加套路化,其实思路是一样的
public int longestPalindromeSubseq(String s) {
if(s==null || s.length()<=0) return 0;
int N=s.length();
int[][] dp=new int[N][N];
//base len=1
for(int i=0;i<N;i++){
dp[i][i]=1;
}
for(int len=2;len<=N;len++){
for(int i=0;i<=N-len;i++){
//j=i+len-1<N
int j=i+len-1;
if(s.charAt(i)==s.charAt(j)){
dp[i][j]=dp[i+1][j-1]+2;
}else{
dp[i][j]=Math.max(dp[i+1][j],dp[i][j-1]);
}
}
}
return dp[0][N-1];
}
解法二
对比一下递归解法是真的简洁,没有那么多边界考虑
//递归解法,自底向上
private Integer[][] cache=null;
public int longestPalindromeSubseq(String s) {
if (s==null || s.length()<=0) {
return 0;
}
int n=s.length();
cache=new Integer[n][n];
return helper(s,0,n-1);
}
public int helper(String s,int left,int right){
if (left>right) {
return 0;
}
if (left==right) {
return 1;
}
if (cache[left][right]!=null) {
return cache[left][right];
}
if (s.charAt(left) == s.charAt(right)) {
return cache[left][right]=helper(s,left+1,right-1)+2; //由外向内缩进
}
return cache[left][right]=Math.max(helper(s,left+1,right),helper(s,left,right-1));
}
解法三
将问题转换为 LCS 的问题
//LCS 的解法
public int longestPalindromeSubseq(String s) {
if (s==null || s.length()<=0) {
return 0;
}
int n=s.length();
int[][] dp=new int[n+1][n+1]; //dp[i][j] 代表 s[0,i]~rs[0,j] 的最长子序列
String rs=new StringBuilder(s).reverse().toString();
for (int i=1;i<=s.length();i++) {
for (int j=1;j<=rs.length();j++) {
if (s.charAt(i-1)==rs.charAt(j-1)) {
dp[i][j]=dp[i-1][j-1]+1;
}else{
dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[n][n];
}
最长的回文序列其实就是求这个字符串和它翻转后的字符串的最长公共子序列!很妙的解法
1312. 让字符串成为回文串的最少插入次数
给你一个字符串 s ,每一次操作你都可以在字符串的任意位置插入任意字符。
请你返回让 s 成为回文串的 最少操作次数 。
「回文串」是正读和反读都相同的字符串。
示例 1:
输入:s = "zzazz"
输出:0
解释:字符串 "zzazz" 已经是回文串了,所以不需要做任何插入操作。
示例 2:
输入:s = "mbadm"
输出:2
解释:字符串可变为 "mbdadbm" 或者 "mdbabdm" 。
示例 3:
输入:s = "leetcode"
输出:5
解释:插入 5 个字符后字符串变为 "leetcodocteel" 。
示例 4:
输入:s = "g"
输出:0
示例 5:
输入:s = "no"
输出:1
提示:
- 1 <= s.length <= 500
- s 中所有字符都是小写字母。
解法一
170 周赛的压轴题,其实和前面的 516. 最长回文子序列是一样的。没啥好说的
public int minInsertions(String s) {
if (s==null || s.length()<=0) {
return 0;
}
int n=s.length();
int[][] dp=new int[n][n];
for (int i=n-1;i>=0;i--) {
for (int j=i+1;j<n;j++) {
if (s.charAt(i) == s.charAt(j)) {
dp[i][j]=dp[i+1][j-1];
}else{
//不相等就可以在头部插入 s[j] 或者尾部插入 s[i]
//头部插入 s[j] 则子区间就是 dp[i][j-1]
//尾部插入 s[i] 则子区间就是 dp[i+1][j]
dp[i][j]=1+Math.min(dp[i+1][j],dp[i][j-1]);
}
}
}
return dp[0][n-1];
}
解法二
UPDATE:2020.5.18,区间 dp 的写法
public int minInsertions(String s) {
int[][] dp=new int[s.length()][s.length()];
for(int len=2;len<=s.length();len++){
for(int left=0;left+len-1<s.length();left++){
int right=left+len-1;
if(s.charAt(left)==s.charAt(right)){
dp[left][right]=dp[left+1][right-1];
}else{
dp[left][right]=Math.min(dp[left][right-1],dp[left+1][right])+1;
}
}
}
return dp[0][s.length()-1];
}
这题也可以用 LCS 的解法解,n-lcs[n][n]就是最少的插入次数
664. 奇怪的打印机
有台奇怪的打印机有以下两个特殊要求:
打印机每次只能打印同一个字符序列。 每次可以在任意起始和结束位置打印新字符,并且会覆盖掉原来已有的字符。 给定一个只包含小写英文字母的字符串,你的任务是计算这个打印机打印它需要的最少次数。
示例 1:
输入:"aaabbb"
输出:2
解释:首先打印 "aaa" 然后打印 "bbb"。
示例 2:
输入:"aba"
输出:2
解释:首先打印 "aaa" 然后在第二个位置打印 "b" 覆盖掉原来的字符 'a'。
提示: 输入字符串的长度不会超过 100。
解法一
前一天看了大致的思路,隔了一天独立的写了一下,将前天思路的很多细节都想明白了
public int strangePrinter(String s) {
if(s==null || s.length()<=0) return 0;
int N=s.length();
int[][] dp=new int[N][N];
for (int i=0;i<N;i++) {
dp[i][i]=1;
}
//aa 1
//aab 2
//aaba 2
//aabab 3
//aababa 4
for (int len=2;len<=N;len++) {
for (int left=0;left+len-1<N;left++) { //左端点
int right=left+len-1; //右端点
//和前一个区间 [left,right-1] 的第一个字符相等,可以直接顺带打印出来
if(s.charAt(right)==s.charAt(left)){
//至少是 dp[left][right-1]
dp[left][right]=dp[left][right-1];
continue;
}
//最多是前一个区间+1(直接打印 right 位置的字符)
dp[left][right]=dp[left][right-1]+1;
//枚举 [left,right) 中的所有字符,如果有和 right 相等的就考虑从这个位置分割整个字符
//比如 abc b 这个最后的 b 就可以连同前面的 bc 一起顺带打印出来
//所以当前区间的值就是可以是 dp[a][a]+dp[b][c], 我们从所有的这种情况中取最小值就 ok 了
for (int i=left;i<right;i++) {
if(s.charAt(right)==s.charAt(i)){
dp[left][right]=Math.min(dp[left][i-1]+dp[i][right-1],dp[left][right]);
}
}
}
}
return dp[0][N-1];
}
dp[left][right]代表 left 到 right 的最少打印次数,然后我们要理解一点:dp[left][right] 其实只可能有两个取值,dp[left][right-1]或者dp[left][right-1]+1,我们求最小打印次数其实就是希望增加一个字符后打印次数不变
eg: abc b 这个最后的 b 就可以连同前面的 bc 一起顺带打印出来,打印次数不变
枚举所有的区间[left,right],然后枚举区间[left,right-1]内的字符,如果区间[left,right-1]内的某个字符i和right相等,那么right就可以跟随[i,right-1]一起顺带打印出来,这样该区间的 dp 值为
dp[left][right]=dp[left][i-1]+dp[i][right-1]
这样就有可能让打印次数不变,我们求一下所有情况的最小值就可以了
这题的代码还可以更简洁,不过我懒得改了,感觉上面的代码已经很清晰了
ps: 这几天做了不少有点难度的 DP 题,发现确实自己对边界的处理,递推公式的理解有了一点提升,加油💪
1547. 切棍子的最小成本
Difficulty: 困难
有一根长度为 n 个单位的木棍,棍上从 0 到 n 标记了若干位置。例如,长度为 6 的棍子可以标记如下:
给你一个整数数组 cuts ,其中 cuts[i] 表示你需要将棍子切开的位置。
你可以按顺序完成切割,也可以根据需要更改切割的顺序。
每次切割的成本都是当前要切割的棍子的长度,切棍子的总成本是历次切割成本的总和。对棍子进行切割将会把一根木棍分成两根较小的木棍(这两根木棍的长度和就是切割前木棍的长度)。请参阅第一个示例以获得更直观的解释。
返回切棍子的 最小总成本 。
示例 1:
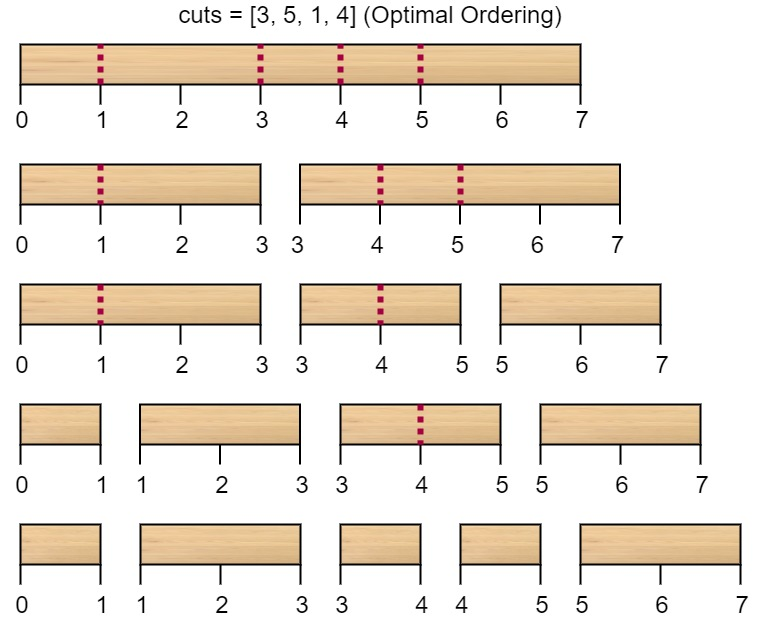
输入:n = 7, cuts = [1,3,4,5]
输出:16
解释:按 [1, 3, 4, 5] 的顺序切割的情况如下所示:
第一次切割长度为 7 的棍子,成本为 7 。第二次切割长度为 6 的棍子(即第一次切割得到的第二根棍子),第三次切割为长度 4 的棍子,最后切割长度为 3 的棍子。总成本为 7 + 6 + 4 + 3 = 20 。
而将切割顺序重新排列为 [3, 5, 1, 4] 后,总成本 = 16(如示例图中 7 + 4 + 3 + 2 = 16)。
示例 2:
输入:n = 9, cuts = [5,6,1,4,2]
输出:22
解释:如果按给定的顺序切割,则总成本为 25 。总成本 <= 25 的切割顺序很多,例如,[4,6,5,2,1] 的总成本 = 22,是所有可能方案中成本最小的。
提示:
2 <= n <= 10^61 <= cuts.length <= min(n - 1, 100)1 <= cuts[i] <= n - 1cuts数组中的所有整数都 互不相同
解法一
201th 周赛的 t4,感觉还是挺简单的,今天补的时候花了 10 分钟搞清楚思路,一遍看视频一边写,最后不出意外的的 T 了~😂一开始没想清楚细节,想到了以区间开始和结尾做 dp,然后就直接开了个 n*n 的数组,虽然是对的,但是在初始化的时候就 t 了,这里实际上只需要开一个 len(cuts)^2 的空间就行了
func minCost(n int, cut []int) int {
sort.Ints(cut)
//在前后加上 0 和 n
cut = append(cut, n)
cut = append([]int{0}, cut...)
var Min = func(a,b int) int {if a<b {return a};return b}
var m = len(cut)
//dp[i][j] 切割 i,j 的成本
var dp = make([][]int, m)
for i := 0; i < m; i++ {
dp[i] = make([]int, m)
if i < m-1 {
dp[i][i+1] = 0
}
}
for tlen := 2; tlen <= m; tlen++ {
for left := 0; left+tlen < m; left++ {
right := left+tlen //注意这里不加 1
dp[left][right] = math.MaxInt32
for k := left+1; k < right; k++ {
dp[left][right] = Min(dp[left][right], dp[left][k]+dp[k][right]+cut[right]-cut[left])
}
}
}
return dp[0][m-1]
}
一开始 tle 的错误代码
func minCost(n int, cut []int) int {
sort.Ints(cut)
//0,1,3,4,5,6
cut = append(cut, n)
cut = append([]int{0}, cut...)
var Min = func(a,b int) int {if a<b {return a};return b}
var m = len(cut)
var dp = make([][]int, n+1)
for i := 0; i <= n; i++ {
dp[i] = make([]int, n+1) //这里就 t 了
// for j := 0; j <= n; j++ {
// dp[i][j] = math.MaxInt32
// }
}
for i := 0; i < m-1; i++ {
for j := i+1; j < m; j++ {
dp[cut[i]][cut[j]] = 0x3f3f3f3f
}
dp[cut[i]][cut[i+1]] = 0
}
for tlen := 2; tlen <= m; tlen++ {
for left := 0; left+tlen-1 < m; left++ {
right := left+tlen-1
for k := left+1; k < right; k++ {
dp[cut[left]][cut[right]] = Min(dp[cut[left]][cut[right]], dp[cut[left]][cut[k]] + dp[cut[k]][cut[right]] + cut[right]-cut[left])
}
}
}
return dp[0][n]
}
数位 DP
233. 数字 1 的个数
给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。
示例:
输入:13
输出:6
解释:数字 1 出现在以下数字中:1, 10, 11, 12, 13 。
解法一
这个题其实困扰了我很长时间,之前看了好几次都放弃了,感觉有些找规律的数学解法太难想到了,所以这里直接采用数位 DP,相对于其他的解法,这种解法会更加套路模板化
//dp[pos][sumOne] 代表枚举到 pos 位置,前面 1 出现的个数为 sumOne 的时候,pos 到最低位出现的数字 1 的个数
int [][] dp=null;
public int countDigitOne(int n) {
int len=0;
int[] num=new int[64]; //64 位肯定够了
while(n!=0){
num[len++]=n%10;
n/=10;
}
dp=new int[len+1][len+1];
//从高位向低位枚举
return dfs(num,len-1,0,true,true);
}
public int dfs(int[] num,int pos,int sumOne,boolean leadZero,boolean limit){
//枚举完所有的数位,直接返回 sumOne(这个数有多少个 1)
if(pos==-1) return sumOne;
//状态重叠,状态要完全一致
if(!leadZero && !limit && dp[pos][sumOne]!=0) return dp[pos][sumOne];
int res=0;
int up=limit?num[pos]:9;
for (int i=0;i<=up;i++) {
res+=dfs(num,pos-1,sumOne+(i==1?1:0),leadZero&&i==0,i==up&&limit);
}
if(!leadZero && !limit) dp[pos][sumOne]=res;
return res;
}
优化下代码,前导 0 对状态存取没有影响,这里考虑的是数字的组成
//简化下代码,前导 0 其实没有影响
//dp[pos][sumOne] 代表从高位枚举到 pos 位置,前面 1 的个数 sumOne 时
int [][] dp=null;
public int countDigitOne(int n) {
int len=0;
int[] num=new int[64]; //64 位肯定够了
while(n!=0){
num[len++]=n%10;
n/=10;
}
dp=new int[len+1][len+1];
//从高位向低位枚举
return dfs(num,len-1,0,true);
}
public int dfs(int[] num,int pos,int sumOne,boolean limit){
//枚举完所有的数位,直接返回 sumOne
if(pos==-1) return sumOne;
//状态重叠,状态要完全一致
if(!limit && dp[pos][sumOne]!=0) return dp[pos][sumOne];
int res=0;
int up=limit?num[pos]:9;
for (int i=0;i<=up;i++) {
res+=dfs(num,pos-1,sumOne+(i==1?1:0),i==up&&limit);
}
if(!limit) dp[pos][sumOne]=res;
return res;
}
Update: 2020.6.24
用 go 重写了下,同时发现之前对这个状态的理解是错的。
func countDigitOne(n int) int {
var nums []int
for n > 0 {
nums = append(nums, n%10)
n /= 10
}
dp := make([][]int, len(nums))
for i := 0; i < len(dp); i++ {
dp[i] = make([]int, len(nums))
}
return dfs(len(nums)-1, 0, true, nums, dp)
}
func dfs(pos int, cnt int, limit bool, nums []int, dp [][]int) int {
if pos == -1 {
return cnt
}
if !limit && dp[pos][cnt] != 0 {
return dp[pos][cnt]
}
var up = 9
if limit {
up = nums[pos]
}
var res = 0
for i := 0; i <= up; i++ {
if i == 1 {
res += dfs(pos-1, cnt+1, i == up && limit, nums, dp)
} else {
res += dfs(pos-1, cnt, i == up && limit, nums, dp)
}
}
if !limit {
dp[pos][cnt] = res
}
return res
}
这里cnt指的其实是[最高位 ~ pos 位]的 1 出现的个数,当 pos 为-1 的时候其实就是到达了某一个具体的数字,比如1231这个时候就会返回cnt=2,与此同时,cnt 也是状态的一部分,比如n=1200 , pos=1 , cnt=1表示枚举到了第 1 位出现了 1 个 1,就说明高两位1出现了 1 次,也就是10或者01,这个时候当我们先求出了01xx(0100 ~ 0199)中的 1 的个数的时候,我们保存这个状态,当前我们下次再遇到这个状态的时候,也就是10xx的时候,我们就可以直接将前面01xx的 dp 值返回,因为01xx和10xx包含的 1 的数量肯定是一样的,无需重复计算
**数位 DP 的概念和模板其实我也是下午在网上查的,然后找到了两个写的比较好的文章 数位 dp 总结 之 从入门到模板,数字组成的奥妙——数位 dp 以后遇到类似的题又多了一种解法(数学的解法至今仍没学会🤣)只有这一题想搞懂数位 DP **还是不太够,这题还是比较简单的,还是要多做题,多总结才能慢慢体会,lc 上好像数位 dp 好像并不多,过两天都做一下试试
1420. 生成数组
给你三个整数 n、m 和 k 。下图描述的算法用于找出正整数数组中最大的元素。

请你生成一个具有下述属性的数组 arr :
- arr 中有 n 个整数。
- 1 <= arr[i] <= m 其中 (0 <= i < n) 。
- 将上面提到的算法应用于 arr ,search_cost 的值等于 k 。
返回上述条件下生成数组 arr 的 方法数 ,由于答案可能会很大,所以 必须 对 10^9 + 7 取余。
示例 1:
输入:n = 2, m = 3, k = 1
输出:6
解释:可能的数组分别为 [1, 1], [2, 1], [2, 2], [3, 1], [3, 2] [3, 3]
示例 2:
输入:n = 5, m = 2, k = 3
输出:0
解释:没有数组可以满足上述条件
示例 3:
输入:n = 9, m = 1, k = 1
输出:1
解释:可能的数组只有 [1, 1, 1, 1, 1, 1, 1, 1, 1]
示例 4:
输入:n = 50, m = 100, k = 25
输出:34549172
解释:不要忘了对 1000000007 取余
示例 5:
输入:n = 37, m = 17, k = 7
输出:418930126
提示:
- 1 <= n <= 50
- 1 <= m <= 100
- 0 <= k <= n
解法一
185 周赛 T4,类似于数位 DP,记忆化递归的方式很好理解
int mod=(int)1e9+7;
Integer [][][] dp=null;
public int numOfArrays(int n, int m, int k) {
dp=new Integer[n+1][m+1][k+1];
return dfs(n,0,m,k);
}
public int dfs(int pos,int preMax,int m,int k){
if(k==0 && pos==0) return dp[pos][preMax][k]=1;
//k=0 但是 pos 不为 0 并没有结束,还可以继续找比 preMax 小的元素
//if(pos==0 || k==0) return 0;
if(pos==0 || k<0) return 0;
if(dp[pos][preMax][k]!=null){
return dp[pos][preMax][k];
}
long res=0;
for (int i=1;i<=m;i++) {
if(i>preMax){ //大于 preMax, 代价-1, 更新最大值
res=(res+dfs(pos-1,i,m,k-1))%mod;
}else{ //小于 preMax, 代价不变,最大值不变
res=(res+dfs(pos-1,preMax,m,k))%mod;
}
}
return dp[pos][preMax][k]=(int)(res%mod);
}
一开始没注意给 dp 数组赋初始值,直接按照 0 判断的,结果 T 了半天,我都懵了了,后来才意识到,很多状态的结果就是 0,你直接按照 0 判断,很多相同的 dp 值为 0 的状态都没有被取出来用
优化
int mod=(int)1e9+7;
Long [][][] dp=null;
public int numOfArrays(int n, int m, int k) {
dp=new Long[n+1][m+1][k+1];
return (int)dfs(n,0,m,k);
}
public long dfs(int pos,int preMax,int m,int k){
if(k==0 && pos==0) return dp[pos][preMax][k]=1L;
//k=0 但是 pos 不为 0 并没有结束,还可以继续找比 preMax 小的元素
//if(pos==0 || k==0) return 0;
if(pos==0 || k<0) return 0L;
if(dp[pos][preMax][k]!=null){
return dp[pos][preMax][k];
}
long res=0;
//小于等于 preMax 的部分可以通过 dfs(pos-1,preMax,m,k) 算出来,减少递归次数
res=(res+(preMax*dfs(pos-1,preMax,m,k))%mod)%mod;
for (int i=preMax+1;i<=m;i++) {
res=(res+dfs(pos-1,i,m,k-1))%mod;
}
return dp[pos][preMax][k]=res%mod;
}
解法二
递推的方式,其实思想是一样的,但是个人感觉并不是特别容易直接想出来
public int numOfArrays(int n, int m, int k) {
int mod=1000_000_007;
long[][][] dp=new long[n+1][m+1][k+1];
for(int i=1;i<=m;i++){
dp[1][i][1]=1;
}
for(int i=2;i<=n;i++){
for(int j=1;j<=m;j++){
for(int cost=1;cost<=k;cost++){
//新增加的元素小于等于 j 也就是原数组的最大值,对应上面递归的 i<=preMax
//所以新增加的元素在新数组的末尾有 1~j 种选择
dp[i][j][cost]=(j*dp[i-1][j][cost])%mod;
for(int nm=1;nm<j;nm++){
//新增加的元素大于原数组的最大值 j, 对应上面递归的 i>preMax
dp[i][j][cost]=(dp[i][j][cost]+dp[i-1][nm][cost-1])%mod;
}
}
}
}
long res=0;
for(int i=1;i<=m;i++){
res+=dp[n][i][k];
res%=mod;
}
return (int)(res%mod);
}
902. 最大为 N 的数字组合
Difficulty: 困难
我们有一组排序的数字 D,它是 {'1','2','3','4','5','6','7','8','9'} 的非空子集。(请注意,'0' 不包括在内。)
现在,我们用这些数字进行组合写数字,想用多少次就用多少次。例如 D = {'1','3','5'},我们可以写出像 '13', '551', '1351315' 这样的数字。
返回可以用 D 中的数字写出的小于或等于 N 的正整数的数目。
示例 1:
输入:D = ["1","3","5","7"], N = 100
输出:20
解释:
可写出的 20 个数字是:
1, 3, 5, 7, 11, 13, 15, 17, 31, 33, 35, 37, 51, 53, 55, 57, 71, 73, 75, 77.
示例 2:
输入:D = ["1","4","9"], N = 1000000000
输出:29523
解释:
我们可以写 3 个一位数字,9 个两位数字,27 个三位数字,
81 个四位数字,243 个五位数字,729 个六位数字,
2187 个七位数字,6561 个八位数字和 19683 个九位数字。
总共,可以使用 D 中的数字写出 29523 个整数。
提示:
D是按排序顺序的数字'1'-'9'的子集。1 <= N <= 10^9
解法一
lc 上写的第 3 道数位 DP,套模板,理解的还不够深刻,等以后做多了再单独开专题讲解
boolean[] dict;
int[] nums;
Integer[] dp;
public int atMostNGivenDigitSet(String[] D, int N) {
int pos = -1;
nums = new int[64];
while (N > 0) {
nums[++pos] = N % 10;
N /= 10;
}
dict = new boolean[10];
dp = new Integer[pos + 1];
for (int i = 0; i < D.length; i++) {
dict[Integer.valueOf(D[i])] = true;
}
return dfs(pos, true, true);
}
//从 pos~0 有多少个合法的数
public int dfs(int pos, boolean leadZero, boolean limit) {
if (pos == -1) {
//枚举完所有的数位,没有前导 0 说明找到了一个合法的数
return leadZero ? 0 : 1;
}
if (!leadZero && !limit && (dp[pos] != null)) {
return dp[pos];
}
int res = 0;
int up = limit ? nums[pos] : 9;
for (int i = 0; i <= up; i++) {
//前面全是 0 || 当前位在 dict 中
if ((leadZero && (i == 0)) || dict[i]) {
res += dfs(pos - 1, leadZero && (i == 0), limit && (i == up));
}
}
if (!leadZero && !limit) {
dp[pos] = res;
}
return res;
}
状压 DP
464. 我能赢吗
在 “100 game” 这个游戏中,两名玩家轮流选择从 1 到 10 的任意整数,累计整数和,先使得累计整数和达到 100 的玩家,即为胜者。
如果我们将游戏规则改为 “玩家不能重复使用整数” 呢?
例如,两个玩家可以轮流从公共整数池中抽取从 1 到 15 的整数(不放回),直到累计整数和 >= 100。
给定一个整数 maxChoosableInteger (整数池中可选择的最大数)和另一个整数 desiredTotal(累计和),判断先出手的玩家是否能稳赢(假设两位玩家游戏时都表现最佳)?
你可以假设 maxChoosableInteger 不会大于 20, desiredTotal 不会大于 300。
示例:
输入:
maxChoosableInteger = 10
desiredTotal = 11
输出:
false
解释:
无论第一个玩家选择哪个整数,他都会失败。
第一个玩家可以选择从 1 到 10 的整数。
如果第一个玩家选择 1,那么第二个玩家只能选择从 2 到 10 的整数。
第二个玩家可以通过选择整数 10(那么累积和为 11 >= desiredTotal),从而取得胜利。
同样地,第一个玩家选择任意其他整数,第二个玩家都会赢。
解法一
从 力扣上的 DP 问题分类汇总 过来的,所以首先知道这个是状压 DP,但是菜鸡的我并不知道状压 DP 是啥🤣,所以先写了个暴力的搜索,然后不出意料的 t 了
//TLE case 20 210 41/45
public boolean canIWin(int maxChoosableInteger, int desiredTotal) {
if(desiredTotal<=maxChoosableInteger) return true;
if((1+maxChoosableInteger)*(maxChoosableInteger)/2<desiredTotal) return false;
boolean[] visit=new boolean[maxChoosableInteger+1];
return dfs(maxChoosableInteger,desiredTotal,visit);
}
public boolean dfs(int max,int total,boolean[] visit){
if(total<=0) return false; //前人已经拿完了
for (int i=1;i<=max;i++) {
if(!visit[i]){
visit[i]=true;
boolean temp=dfs(max,total-i,visit);
visit[i]=false;
if(!temp){
return true;
}
}
}
return false;
}
注意这个写法的返回时机,有些语句是不能合并的,比如下面这样就是错的(别问我为啥知道的🤣)
public boolean dfs(int max,int total,boolean[] visit){
if(total<=0) return false;
for (int i=1;i<=max;i++) {
if(!visit[i]){
visit[i]=true;
if(!dfs(max,total-i,visit)){
return true;
}
visit[i]=false;
}
}
return false;
}
像上面这样写乍一看好像没问题,对比一下两种写法,其实就是回溯visit的时机不同,第一个是另一个人dfs 不管成功与否都会回溯状态,而第二种是另一个人dfs 成功后才会回溯状态,失败后就不会回溯状态了,但是在这题中不管另一个人失败与否都需要回溯状态,首先另一个人成功后我肯定是要回溯,另一个人成功意味着我失败了,我还要继续尝试找必胜的选取方法,但是另一个人失败后还是需要回溯状态,仔细想想,下一层 dfs(另一个人)失败是因为下下一层 dfs(我)成功了,我在那一次成功后并没有回溯visit,这样下一层(另一个人)就用不了被下下层占用的数字,就无法枚举所有情况,自然就错了
各位大佬见谅,表达能力有限,上面的都是我胡言乱语,大佬们跳过就行了
解法二
根据昨天写的一个数位 DP,加上自己的 yy,写了个状压 DP 出来了🤣,上面的解法明显会有很多的重复解,而确定是否重复的关键其实就是数字的选取情况,上面我们是用的一个visit数组来记录这选取的情况,要直接通过这个visit来判断状态是否相同是很耗时耗力的,所以就引入了状态压缩,我们可以用二进制的第i位的 0 或者 1 来表示i这个数字的选取与否,这样所有数字的选取状态就可以用一个数来很方便的表示,题目说了不超过 20 位,所以这里就可以用一个int来表示状态state,通过state来判断状态是否一致,进而进行记忆化的存取
Boolean[] dp=null; //用 Boolean 比较方便判断是否记忆化
public boolean canIWin(int maxChoosableInteger, int desiredTotal) {
//小于最大值先手可以直接拿
if(desiredTotal<=maxChoosableInteger) return true;
//前 N 项和还不够 desiredTotal
if((1+maxChoosableInteger)*(maxChoosableInteger)/2<desiredTotal) return false;
//20 位二进制 1<<21
dp=new Boolean[1<<21];
return dfs(maxChoosableInteger,desiredTotal,0);
}
public boolean dfs(int max,int total,int state){
if(total<=0) return false; //前人已经拿完了
if(dp[state]!=null){
return dp[state];
}
for (int i=max;i>=1;i--) {
//参数传递的,就不用回溯了,代码变的简洁多了
if((state>>i&1)==0 && !dfs(max,total-i,state|(1<<i))){
return dp[state]=true;
}
}
return dp[state]=false;
}
其实一开始开了个二维的 new Boolean[desiredTotal] [1<<21],然后就直接 MLE 了😅 太菜了 hahaha,然后看了下,发现state一样的话,total肯定是一样的(反过来就不一定了),所以只需要一维的就可以了
其实也可以用int[]做状压
//int 做状压,似乎性能没有提升
int[] dp=null; //0: 未初始化 1:true 2:false
public boolean canIWin(int maxChoosableInteger, int desiredTotal) {
//小于最大值先手可以直接拿
if(desiredTotal<=maxChoosableInteger) return true;
//前 N 项和还不够 desiredTotal
if((1+maxChoosableInteger)*(maxChoosableInteger)/2<desiredTotal) return false;
//20 位二进制 1<<21
dp=new int[1<<21];
return dfs(maxChoosableInteger,desiredTotal,0);
}
public boolean dfs(int max,int total,int state){
if(dp[state]!=0){
return dp[state]==1;
}
for (int i=max;i>=1;i--) {
//参数传递的,就不用回溯了,代码变的简洁多了
if((state>>i&1)==0 && (i>=total || !dfs(max,total-i,state|(1<<i)))){
dp[state]=1;
return true;
}
}
dp[state]=2;
return false;
}
博弈 DP
292. Nim 游戏
你和你的朋友,两个人一起玩 Nim 游戏:桌子上有一堆石头,每次你们轮流拿掉 1 - 3 块石头。 拿掉最后一块石头的人就是获胜者。你作为先手。
你们是聪明人,每一步都是最优解。 编写一个函数,来判断你是否可以在给定石头数量的情况下赢得游戏。
示例:
输入:4
输出:false
解释:如果堆中有 4 块石头,那么你永远不会赢得比赛;
因为无论你拿走 1 块、2 块 还是 3 块石头,最后一块石头总是会被你的朋友拿走。
解法一
博弈型动态规划入门题
public boolean canWinNim(int n) {
boolean[] dp=new boolean[n];
dp[0]=true;
dp[1]=true;
dp[2]=true;
//t t t f t t t f .....
//每个状态取决于前 3 个状态
for (int i=3;i<n;i++) {
//分别拿 1,2,3 个看对面能不能赢
dp[i]=!dp[i-1] || !dp[i-2] || !dp[i-3];
}
return dp[n-1];
}
这个解法在数据过大的时候还是会 TLE
解法二
规律
public boolean canWinNim(int n) {
return n%4!=0;
}
1025. 除数博弈
Difficulty: 简单
爱丽丝和鲍勃一起玩游戏,他们轮流行动。爱丽丝先手开局。
最初,黑板上有一个数字 N 。在每个玩家的回合,玩家需要执行以下操作:
- 选出任一
x,满足0 < x < N且N % x == 0。 - 用
N - x替换黑板上的数字N。
如果玩家无法执行这些操作,就会输掉游戏。
只有在爱丽丝在游戏中取得胜利时才返回 True,否则返回 false。假设两个玩家都以最佳状态参与游戏。
示例 1:
输入:2
输出:true
解释:爱丽丝选择 1,鲍勃无法进行操作。
示例 2:
输入:3
输出:false
解释:爱丽丝选择 1,鲍勃也选择 1,然后爱丽丝无法进行操作。
提示:
1 <= N <= 1000
解法一
博弈 DP,和上面的类似,尝试所有情况
func divisorGame(N int) bool {
//N=i 时,先手的人能否赢
var dp = make([]bool, N+1)
dp[1] = false
for i := 2; i <= N; i++ {
//尝试所有可行的选择
//从 i 中先手拿 j,看对方在 i-j 中先手能不能赢
for j := 1; j < i; j++ {
if i%j == 0 && !dp[i-j] {
dp[i] = true
break
}
}
}
return dp[N]
}
解法二
很明显,这题也有一个数学的解法😂,利用奇数和偶数的性质,N 为偶数的时候,先手的人是必赢的
//规律,偶数必赢,奇数必输
//最后在 N=2 的时候结束比赛,所以谁先到 2 谁就赢
//奇数的因子只有奇数,奇数-奇数 = 偶数,当我拿到偶数时候可以直接拿走 1,变为奇数,如此往来
//最终我必定能先到 2
func divisorGame(N int) bool {
return N%2 == 0
}
1140. 石子游戏 II
Difficulty: 中等
亚历克斯和李继续他们的石子游戏。许多堆石子 排成一行,每堆都有正整数颗石子 piles[i]。游戏以谁手中的石子最多来决出胜负。
亚历克斯和李轮流进行,亚历克斯先开始。最初,M = 1。
在每个玩家的回合中,该玩家可以拿走剩下的 前 X 堆的所有石子,其中 1 <= X <= 2M。然后,令 M = max(M, X)。
游戏一直持续到所有石子都被拿走。
假设亚历克斯和李都发挥出最佳水平,返回亚历克斯可以得到的最大数量的石头。
示例:
输入:piles = [2,7,9,4,4]
输出:10
解释:
如果亚历克斯在开始时拿走一堆石子,李拿走两堆,接着亚历克斯也拿走两堆。在这种情况下,亚历克斯可以拿到 2 + 4 + 4 = 10 颗石子。
如果亚历克斯在开始时拿走两堆石子,那么李就可以拿走剩下全部三堆石子。在这种情况下,亚历克斯可以拿到 2 + 7 = 9 颗石子。
所以我们返回更大的 10。
提示:
1 <= piles.length <= 1001 <= piles[i] <= 10 ^ 4
解法一
瞎写的记忆化,懒得改 dp 了
int n = 0;
Integer[][] cache;
public int stoneGameII(int[] piles) {
n = piles.length;
//这里用后缀和会简单一点,懒得改了
int[] preSum = new int[n+1];
cache = new Integer[n+1][n+1];
preSum[0] = 0;
for(int i = 1; i <=n; i++){
preSum[i] = preSum[i-1] + piles[i-1];
}
return dfs(preSum, 0, 1);
}
public int dfs(int[] preSum, int start, int M){
if(cache[start][M]!=null){
return cache[start][M];
}
int res = 0;
for(int len = 1; start + len - 1 < n && len <= 2*M; len++){
//start=0 len=2 (0,1)
int temp = preSum[n] - preSum[start] - dfs(preSum, start + len, Math.max(M, len));
res = Math.max(res, temp);
}
return cache[start][M] = res;
}
1406. 石子游戏 III
Difficulty: 困难
Alice 和 Bob 用几堆石子在做游戏。几堆石子排成一行,每堆石子都对应一个得分,由数组 stoneValue 给出。
Alice 和 Bob 轮流取石子,Alice 总是先开始。在每个玩家的回合中,该玩家可以拿走剩下石子中的的前 1、2 或 3 堆石子 。比赛一直持续到所有石头都被拿走。
每个玩家的最终得分为他所拿到的每堆石子的对应得分之和。每个玩家的初始分数都是 0 。比赛的目标是决出最高分,得分最高的选手将会赢得比赛,比赛也可能会出现平局。
假设 Alice 和 Bob 都采取 最优策略 。如果 Alice 赢了就返回 “Alice” _,_Bob 赢了就返回 _“Bob”,_平局(分数相同)返回 “Tie” 。
示例 1:
输入:values = [1,2,3,7]
输出:"Bob"
解释:Alice 总是会输,她的最佳选择是拿走前三堆,得分变成 6 。但是 Bob 的得分为 7,Bob 获胜。
示例 2:
输入:values = [1,2,3,-9]
输出:"Alice"
解释:Alice 要想获胜就必须在第一个回合拿走前三堆石子,给 Bob 留下负分。
如果 Alice 只拿走第一堆,那么她的得分为 1,接下来 Bob 拿走第二、三堆,得分为 5 。之后 Alice 只能拿到分数 -9 的石子堆,输掉比赛。
如果 Alice 拿走前两堆,那么她的得分为 3,接下来 Bob 拿走第三堆,得分为 3 。之后 Alice 只能拿到分数 -9 的石子堆,同样会输掉比赛。
注意,他们都应该采取 最优策略 ,所以在这里 Alice 将选择能够使她获胜的方案。
示例 3:
输入:values = [1,2,3,6]
输出:"Tie"
解释:Alice 无法赢得比赛。如果她决定选择前三堆,她可以以平局结束比赛,否则她就会输。
示例 4:
输入:values = [1,2,3,-1,-2,-3,7]
输出:"Alice"
示例 5:
输入:values = [-1,-2,-3]
输出:"Tie"
提示:
1 <= values.length <= 50000-1000 <= values[i] <= 1000
解法一
某次双周赛的 T4,没参加,感觉这题还是挺简单的,比 2 还要简单,下面的做法直接套用 2 的做法,改成了后缀和数组
//后缀数组
int[] sufSum = null;
Integer[] dp = null;
public String stoneGameIII(int[] stoneValue) {
int n = stoneValue.length;
sufSum = new int[n+1];
dp = new Integer[n+1];
for (int i = n-1; i >= 0; i--){
sufSum[i] = sufSum[i+1] + stoneValue[i];
}
int alice = dfs(stoneValue, 0);
int bob = sufSum[0]-alice;
if (alice == bob) {
return "Tie";
}
return alice > bob ? "Alice" : "Bob";
}
public int dfs(int[] sv, int start){
if (start > sv.length) {
return 0;
}
if (dp[start]!=null) {
return dp[start];
}
int sum = sufSum[start];
return dp[start] = Math.max(sum-dfs(sv, start+1), Math.max(sum-dfs(sv, start+2), sum-dfs(sv, start+3)));
}
这题还有更好的做法,先挖个坑,后面有时间再写
1510. 石子游戏 IV
Difficulty: 困难
Alice 和 Bob 两个人轮流玩一个游戏,Alice 先手。
一开始,有 n 个石子堆在一起。每个人轮流操作,正在操作的玩家可以从石子堆里拿走 任意 非零 平方数 个石子。
如果石子堆里没有石子了,则无法操作的玩家输掉游戏。
给你正整数 n ,且已知两个人都采取最优策略。如果 Alice 会赢得比赛,那么返回 True ,否则返回 False 。
示例 1:
输入:n = 1
输出:true
解释:Alice 拿走 1 个石子并赢得胜利,因为 Bob 无法进行任何操作。
示例 2:
输入:n = 2
输出:false
解释:Alice 只能拿走 1 个石子,然后 Bob 拿走最后一个石子并赢得胜利(2 -> 1 -> 0)。
示例 3:
输入:n = 4
输出:true
解释:n 已经是一个平方数,Alice 可以一次全拿掉 4 个石子并赢得胜利(4 -> 0)。
示例 4:
输入:n = 7
输出:false
解释:当 Bob 采取最优策略时,Alice 无法赢得比赛。
如果 Alice 一开始拿走 4 个石子, Bob 会拿走 1 个石子,然后 Alice 只能拿走 1 个石子,Bob 拿走最后一个石子并赢得胜利(7 -> 3 -> 2 -> 1 -> 0)。
如果 Alice 一开始拿走 1 个石子, Bob 会拿走 4 个石子,然后 Alice 只能拿走 1 个石子,Bob 拿走最后一个石子并赢得胜利(7 -> 6 -> 2 -> 1 -> 0)。
示例 5:
输入:n = 17
输出:false
解释:如果 Bob 采取最优策略,Alice 无法赢得胜利。
提示:
1 <= n <= 10^5
解法一
前几次双周赛的 T4,太水了,大水题,顶多算 mid
func winnerSquareGame(n int) bool {
var dp = make([]bool, 100001)
dp[0] = false
for i := 1; i <= n; i++ {
for j := 1; j*j <= i; j++ {
if !dp[i-j*j] {
dp[i] = true
break
}
}
}
return dp[n]
}
解法二
玩了一手花哨的记忆化手法😂
//记忆化
func winnerSquareGame(n int) bool {
var T, F = true, false
var dfs func(int) bool
var dp = make([]*bool, 100001)
//先手拿 x^2 个石头
dfs = func (n int) bool {
if dp[n] != nil {
return *dp[n]
}
if n == 0 {
return F
}
for i := 1; i*i <= n; i++{
if !dfs(n-i*i) {
dp[n] = &T
return T
}
}
dp[n] = &F
return F
}
return dfs(n)
}
486. 预测赢家
Difficulty: 中等
给定一个表示分数的非负整数数组。 玩家 1 从数组任意一端拿取一个分数,随后玩家 2 继续从剩余数组任意一端拿取分数,然后玩家 1 拿,…… 。每次一个玩家只能拿取一个分数,分数被拿取之后不再可取。直到没有剩余分数可取时游戏结束。最终获得分数总和最多的玩家获胜。
给定一个表示分数的数组,预测玩家 1 是否会成为赢家。你可以假设每个玩家的玩法都会使他的分数最大化。
示例 1:
输入:[1, 5, 2]
输出:False
解释:一开始,玩家 1 可以从 1 和 2 中进行选择。
如果他选择 2(或者 1 ),那么玩家 2 可以从 1(或者 2 )和 5 中进行选择。如果玩家 2 选择了 5 ,那么玩家 1 则只剩下 1(或者 2 )可选。
所以,玩家 1 的最终分数为 1 + 2 = 3,而玩家 2 为 5 。
因此,玩家 1 永远不会成为赢家,返回 False 。
示例 2:
输入:[1, 5, 233, 7]
输出:True
解释:玩家 1 一开始选择 1 。然后玩家 2 必须从 5 和 7 中进行选择。无论玩家 2 选择了哪个,玩家 1 都可以选择 233 。
最终,玩家 1(234 分)比玩家 2(12 分)获得更多的分数,所以返回 True,表示玩家 1 可以成为赢家。
提示:
- 1 <= 给定的数组长度 <= 20.
- 数组里所有分数都为非负数且不会大于 10000000 。
- 如果最终两个玩家的分数相等,那么玩家 1 仍为赢家。
解法一
记忆化,这种博弈的题目记忆化写起来会比较自然
func PredictTheWinner(nums []int) bool {
var Max = func(a, b int) int {if a > b {return a};return b}
var n = len(nums)
var preSum = make([]int, n+1)
for i := 1; i <= n; i++ {
preSum[i] = preSum[i-1] + nums[i-1]
}
//记忆化
var dp = make([][]int, n)
for i := 0; i < n; i++ {
dp[i] = make([]int, n)
for j := 0; j < n; j++ {
dp[i][j] = -1
}
}
var dfs func(i int, j int) int
dfs = func(i int, j int) int {
if dp[i][j] != -1 {
return dp[i][j]
}
if i == j {
return nums[i]
}
//区间和
sum := preSum[j+1] - preSum[i]
dp[i][j] = Max(sum-dfs(i+1, j), sum-dfs(i, j-1))
return dp[i][j]
}
A := dfs(0, n-1)
return A >= preSum[n]-A
}
解法二
区间 DP 的写法当然也可以,思路一样
func PredictTheWinner(nums []int) bool {
var n = len(nums)
var dp = make([][]int, n)
var Max = func(a,b int) int {if a>b {return a};return b}
for i := 0; i < n; i++ {
dp[i] = make([]int, n)
dp[i][i] = nums[i]
}
var preSum = make([]int, n+1)
for i := 1; i <= n; i++ {
preSum[i] = preSum[i-1] + nums[i-1]
}
for tlen := 2; tlen <= n; tlen++ {
for left := 0; left+tlen-1 < n; left++ {
right := left+tlen-1
sum := preSum[right+1]-preSum[left]
dp[left][right] = Max(sum-dp[left][right-1], sum-dp[left+1][right])
}
}
return dp[0][n-1] >= preSum[n]-dp[0][n-1]
}
图论
暂时先放在这里,等后面学了 dij,spfa 那些后一起单独总结一下
743. 网络延迟时间
有 N 个网络节点,标记为 1 到 N。
给定一个列表 times,表示信号经过有向边的传递时间。 times[i] = (u, v, w),其中 u 是源节点,v 是目标节点, w 是一个信号从源节点传递到目标节点的时间。
现在,我们从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号?如果不能使所有节点收到信号,返回 -1。
示例:
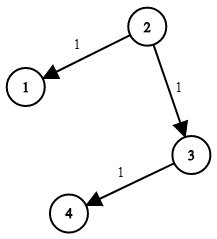
输入:times = [[2,1,1],[2,3,1],[3,4,1]], N = 4, K = 2
输出:2
注意:
N的范围在[1, 100]之间。K的范围在[1, N]之间。times的长度在[1, 6000]之间。- 所有的边
times[i] = (u, v, w)都有1 <= u, v <= N且0 <= w <= 100。
解法一
临时起意学了下 Floyd,然后在 lc 上搜了一下找到了这一题,思路也很直接
//Floyd
public int networkDelayTime(int[][] times, int N, int K) {
int[][] dis=new int[N][N];
int INF = 0x3f3f3f3f;
for(int i=0;i<N;i++) Arrays.fill(dis[i],INF);
for(int i=0;i<N;i++) dis[i][i]=0;
for(int[] t:times) dis[t[0]-1][t[1]-1]=t[2];
for(int k=0;k<N;k++){
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
dis[i][j]=Math.min(dis[i][j],dis[i][k]+dis[k][j]);
}
}
}
int res=0;
K-=1; //从 0 开始!从 1 开始的都是邪教
for(int i=0;i<N;i++){
if(dis[K][i]==INF) return -1;
res=Math.max(dis[K][i],res);
}
return res;
}
大概说一下,其实 Floyd 就是动态规划的思想,dp[k][i][j]代表从i~j允许经过前k个节点中转时的最短路径,那么其实很容易推导出,dp[k][i][j]=min(dp[k-1][i][k]+dp[k-1][k][j],dp[k][i][j])其实也就是尝试以每个点为中转点,看能否缩短两点之间的距离,和区间 DP 有点像,关于k为什么要放外面其实仔细想一下就知道了,我们需要保证在求dp[k][i][j]的时候需要保证dp[k-1][i][j]以及dp[k-1][i][k] 和dp[k-1][k][j]都是已经计算完毕的,想一想,如果 k 放在里面能保证么?很明显不行,可以类比上面的 576. 出界的路径数,一样的道理。然后我们再观察整个递推方程,发现dp[k]只依赖于dp[k-1]所以就可以直接滚动数组优化掉 k 维度的空间,也就是上面的解法
1584. 连接所有点的最小费用
Difficulty: 中等
给你一个points 数组,表示 2D 平面上的一些点,其中 points[i] = [xi, yi] 。
连接点 [xi, yi] 和点 [xj, yj]` 的费用为它们之间的 曼哈顿距离 :xi - xj| + |yi - yj| ,其中 |val| 表示 val 的绝对值。
请你返回将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时,才认为所有点都已连接。
示例 1:
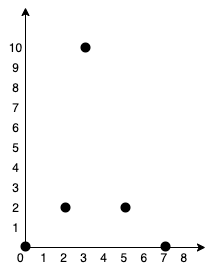
输入:points = [[0,0],[2,2],[3,10],[5,2],[7,0]]
输出:20
解释:
我们可以按照上图所示连接所有点得到最小总费用,总费用为 20 。
注意到任意两个点之间只有唯一一条路径互相到达。
示例 2:
输入:points = [[3,12],[-2,5],[-4,1]]
输出:18
示例 3:
输入:points = [[0,0],[1,1],[1,0],[-1,1]]
输出:4
示例 4:
输入:points = [[-1000000,-1000000],[1000000,1000000]]
输出:4000000
示例 5:
输入:points = [[0,0]]
输出:0
提示:
- 1 <= points.length <= 1000
- -106 <= xi, yi <= 106
- 所有点 (xi, yi) 两两不同。
解法一
Prim O(V^2) 最小生成树,206th 周赛 t3,裸的 mst,但是彩笔的我并不会,事后补了一波 OI Wiki,(这个是原始的暴力 Prim,应对这个题够了)
//Prim O(V^2) 任取一个节作为起点,dis[i] 记录 mst 点集到点 i 的最短距离
//每次取出 mst 点集外 dis[i] 最小的点,也就是离 mst 点集最近的点,并标记为 mst 节点
//然后利用该点更新其他的 mst 点集外的点的 dis 距离,直到将所有的点都加进去,适合稠密图(边数远大于点数)
//可以使用一些数据结构来优化时间复杂度,暂时不深究
public int minCostConnectPoints(int[][] points) {
int INF = 0x3f3f3f3f;
int n = points.length;
//dis 表示 mst 点集到该点的最小距离
int[] dis = new int[n];
Arrays.fill(dis, INF);
dis[0] = 0;
boolean[] vis = new boolean[n];
int res = 0;
for (int i = 0; i < n; i++) {
int minCost = INF;
int k = -1; //最小的新节点
for (int j = 0; j < n; j++) {
if (!vis[j] && dis[j] < minCost) {
minCost = dis[j];
k = j;
}
}
vis[k] = true;
res += minCost;
for (int j = 0; j < n; j++) {
//更新所有 mst 点集外的点的 dis
if (vis[j]) continue;
int mhd = Math.abs(points[k][0]-points[j][0])+Math.abs(points[k][1]-points[j][1]);
dis[j] = Math.min(dis[j], mhd);
}
}
return res;
}
这个题明显是稠密图,用邻接矩阵表示的,Prim 用邻接矩阵时机复杂度就是 O(V^2),V 为点数
数据结构中对于稀疏图的定义为:有很少条边或弧(边的条数|E|远小于|V|²)的图称为稀疏图(sparse graph),反之边的条数|E|接近|V|²,称为稠密图(dense graph)。
解法二
Kruskal + 并查集,比较适合稀疏图,这里时机复杂度是 O(ElogE),E 为边数
//Kruskal+UnionFind
//以边为中心,首先构造出所有的边,然后排序,从最短的边开始,合并该边的两个端点,这里需要用到并查集
//合并 n-1 次后就得到 mst(n 为节点数),适合稀疏图
int[] parent;
int[] rank;
//路径压缩
public int find(int a){
if (parent[a] == a) {
return a;
}
return parent[a] = find(parent[a]);
}
public boolean union(int a, int b) {
int pa = find(a);
int pb = find(b);
if (pa == pb) {
return false;
}
//随便合并 553ms
//parent[pa] = pb;
//按秩合并 564ms 似乎没有什么变化。
if (rank[pa] > rank[pb]) {
parent[pb] = pa;
}else if (rank[pb] > rank[pa]) {
parent[pa] = pb;
}else{
parent[pa] = pb;
rank[pb]++;
}
return true;
}
public int minCostConnectPoints(int[][] points) {
int n = points.length;
parent = new int[n];
rank = new int[n];
//n-1 + n-2 + n-3 +...+ 1 = (n-1) + (n-1)*(n-2)/2 = n(n-1)/2
//5 : 4+3+2+1 = 4*
//0,1: 端点,2: 边权值
int[][] edge = new int[n*(n-1)/2][3];
int idx = 0;
for (int i = 0; i < n; i++) {
for (int j = i+1; j < n; j++) {
int dis = Math.abs(points[i][0]-points[j][0])+Math.abs(points[i][1]-points[j][1]);
edge[idx++] = new int[]{i, j, dis};
}
parent[i] = i;
rank[i] = 1;
}
//按照边的权值排序
Arrays.sort(edge, (e1, e2)->e1[2]-e2[2]);
int res = 0;
int count = 0;
for (int i = 0; i < edge.length; i++) {
if (union(edge[i][0], edge[i][1])) {
res += edge[i][2];
count++;
}
if (count == n-1) {
break;
}
}
return res;
}