LeetCode 二分查找
从 数组专题 中抽取出来的
二分搜索
704. 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入:nums = [-1,0,3,5,9,12], target = 9
输出:4
解释:9 出现在 nums 中并且下标为 4
示例 2:
输入:nums = [-1,0,3,5,9,12], target = 2
输出:-1
解释:2 不存在 nums 中因此返回 -1
提示:
- 你可以假设 nums 中的所有元素是不重复的
- n 将在 [1, 10000] 之间
- nums 的每个元素都将在 [-9999, 9999] 之间
解法一
比较经典的二分
public int search(int[] nums, int target) {
int left=0,right=nums.length;
while(left<right){
int mid=left+(right-left)/2;
if(nums[mid]<target){
left=mid+1;
}else if(nums[mid] > target){
right=mid;
}else{
return mid;
}
}
return -1;
}
解法二
按照板子来的二分,最后需要后处理一下不存在的情况
//模板二分
public int search(int[] nums, int target) {
int left=0,right=nums.length;
while(left<right){
int mid=left+(right-left)/2;
if(nums[mid]<target){ //排除 mid
left=mid+1;
}else{
right=mid;
}
}
return left!=nums.length&&nums[left]==target?left:-1;
}
69. x 的平方根
实现 int sqrt(int x) 函数。
计算并返回 x 的平方根,其中 x 是非负整数。
由于返回类型是整数,结果只保留整数的部分,小数部分将被舍去。
示例 1:
输入:4
输出:2
示例 2:
输入:8
输出:2
说明:8 的平方根是 2.82842...,
由于返回类型是整数,小数部分将被舍去。
解法一
二分解法
func mySqrt(x int) int {
lx := int64(x)
var left int64 = 0
var right int64 = lx/2 + 1
for left < right {
mid := left + (right-left)/2
if mid*mid < lx {
left = mid + 1
//向下取整的,所以需要额外判断或者取右中位数
if left*left > lx {
return int(mid)
}
} else {
right = mid
}
}
return int(left)
}
还有一种比较好的解法,更加贴合模板
//这个其实更能体现模板的好处
func mySqrt(x int) int {
lx := int64(x)
var left int64 = 0
var right int64 = lx/2 + 1
for left < right {
mid := left + (right-left)/2 + 1
//大于 lx 的一定不是 res 可以排除,但是小于的不一定不是,题目是向下取整的
if mid*mid > lx {
right = mid - 1
} else {
left = mid
}
}
return int(left)
}
解法二
牛顿迭代法,还没时间仔细去研究,后面有时间再看看
35. 搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
你可以假设数组中无重复元素。
示例 1:
输入:[1,3,5,6], 5
输出:2
示例 2:
输入:[1,3,5,6], 2
输出:1
示例 3:
输入:[1,3,5,6], 7
输出:4
示例 4:
输入:[1,3,5,6], 0
输出:0
解法一
跟谁学笔试现场写的,上面的都是 dd(删除了之前的解法)
public int searchInsert(int[] nums, int target) {
int len=nums.length;
int lo=0,hi=len; //和模板不一样,因为这里是搜索插入位置是可以到达 right 的
while(lo< hi){
int mid=lo+(hi-lo)/2;
if(nums[mid]<target){
lo=mid+1;
}else {
hi=mid;
}
}
return lo;
}
解法二
//update: 2020.5.18
public int searchInsert(int[] nums, int target) {
int len=nums.length;
int lo=0,hi=len-1;
int res=hi;
while(lo<=hi){
int mid=lo+(hi-lo)/2;
if(nums[mid]>=target){
res=mid;
hi=mid-1;
}else {
lo=mid+1;
}
}
return nums[res]<target?len:res;
}
153. 寻找旋转排序数组中的最小值
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
请找出其中最小的元素。
你可以假设数组中不存在重复元素。
示例 1:
输入:[3,4,5,1,2]
输出:1
示例 2:
输入:[4,5,6,7,0,1,2]
输出:0
解法一
把最开始写的拉跨解法也放上来吧
public int findMin(int[] nums) {
if (nums==null||nums.length<=0) {
return 0;
}
if (nums.length==1||nums[0]<nums[nums.length-1]) {
return nums[0];
}
int left=1,right=nums.length-1;
while(left<right){
int mid=left+(right-left)/2+1;
if (nums[mid]>nums[mid-1]) {
if (nums[mid]>nums[0]) {
left=mid;
}else{
right=mid-1;
}
}else{
return nums[mid];
}
}
return nums[left];
}
说实话,我都不知道咋对的。
解法二
模板解法,还是模板写起来清晰舒服
建议直接看 UPDATE
public int findMin(int[] nums) {
if (nums==null||nums.length<=0) {
return 0;
}
int left=0,right=nums.length-1;
while(left<right){
int mid=left+(right-left)/2;
if (nums[mid]>nums[right]) { //排除 mid 的分支
left=mid+1;
}else{
right=mid;
}
}
return nums[left];
}
需要注意要和右边界比较,和左边界比较不一定正确
比如 1 2 3 4 5 和2 3 4 5 1 两个的中点都大于左边界,但是你无法确定此时应该如果缩短区间,除非做特判,但是那样就麻烦了
UPDATE: 2020.7.22
最小值的特点就是肯定是小于等于 nums 的最后一个元素,这里没有重复的元素,所以最小值肯定是小于最后一个元素的,除非最后一个就是最小的元素,这种情况我们设置为 res 的初始值,这样我重写后我感觉更好理解了,进阶版的只需要在这个的基础上稍加改动就行了
func findMin(nums []int) int {
var n = len(nums)
var left, right = 0, n - 1
var res = right//对 nums[n-1] 就是最小值做兜底
for left <= right {
mid := left + (right-left)/2
if nums[mid] < nums[n-1] {
res = mid
right = mid - 1
} else {
left = mid + 1
}
}
return nums[res]
}
同理也可以和左边界比较,最小值一定是小于等于 nums[0] 的
func findMin(nums []int) int {
var n = len(nums)
var left, right = 0, n - 1
var res = left //对 nums[0] 就是最小值做兜底
for left <= right {
mid := left + (right-left)/2
if nums[mid] < nums[0] {
res = mid
right = mid - 1
} else {
left = mid + 1
}
}
return nums[res]
}
154. 寻找旋转排序数组中的最小值 II
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
请找出其中最小的元素。
注意数组中可能存在重复的元素。
示例 1:
输入:[1,3,5]
输出:1
示例 2:
输入:[2,2,2,0,1]
输出:0
说明:
- 这道题是 寻找旋转排序数组中的最小值 的延伸题目。
- 允许重复会影响算法的时间复杂度吗?会如何影响,为什么?
解法一
建议直接参考解法 2
相比上一题有了重复的元素,在跳转的时候需要分清楚情况,在 mid 和中点相等的时候只排除右边界一个元素
public int findMin(int[] nums) {
int left=0,right=nums.length-1;
while(left<right){
int mid=left+(right-left)/2;
if(nums[mid] > nums[right]){
left=mid+1;
}else if(nums[mid] < nums[right]){
right=mid;
}else{
right--; //和右边界相等,无法判断,只缩减一步
}
}
return nums[left];
}
解法二
(UPDATE: 2020.7.22)
相比 寻找旋转排序数组中的最小值,仅仅只是加了一个尾部去重的操作,去重后就和上面的情况一样了,这样就比前面的解法更加清晰了,时间复杂度也还是一样的
# update: 2020/4/8
class Solution:
def findMin(self, nums: List[int]) -> int:
left, right = 0, len(nums)-1
res = 0
while right >= 0 and nums[right] == nums[0]:
right -= 1
nr = right
while left <= right:
mid = left + (right - left)//2
# 和 nr 比,不能和 0 比,可能会有 0 1 2 这样的
if nums[mid] > nums[nr]:
left = mid + 1
else:
res = mid
right = mid - 1
return nums[res]
33. 搜索旋转排序数组
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
搜索一个给定的目标值,如果数组中存在这个目标值,则返回它的索引,否则返回 -1 。
你可以假设数组中不存在重复的元素。
你的算法时间复杂度必须是 O(log n) 级别。
示例 1:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
示例 2:
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
解法一
题目明确要求了时间复杂度 O(logn),所以肯定还是要二分,先上代码吧
public static int search2(int[] nums, int target) {
int len = nums.length;
if ((nums == null) || (len <= 0)) {
return -1;
}
int lo = 0;
int hi = len - 1;
while (lo <= hi) {
int mid = lo + ((hi - lo) / 2);
// 左,右 指的是旋转点左右
if (nums[mid] > target) { //首先是大于 target 的情况
if (target < nums[lo]) {
//target 在右边
//mid 未知还需要判断下 画一个折线图就很清楚了
if (nums[mid] <= nums[hi]) { //mid 也在右边
hi = mid - 1;
} else {
//mid 在左边
lo = mid + 1;
}
} else if (target > nums[lo]) {
//说明 mid 在左边,target 也在左边
hi = mid - 1;
} else {
return lo;
}
} else if (nums[mid] < target) { //小于 target 的情况
if (target < nums[hi]) {
//mid 在右边,target 在右边
lo = mid + 1;
} else if (target > nums[hi]) {
//target 在左边
//mid 未知还需要判断下
if (nums[mid] > nums[hi]) { //mid 在左边
lo = mid + 1;
} else {
hi = mid - 1;
}
} else {
return hi;
}
} else {
return mid;
}
/*if(hi>=0&&lo<len&&nums[lo]<nums[hi]){
//切换成有序的二分
while(lo<=hi){
mid=lo+(hi-lo)/2;
if(nums[mid]>target){
hi=mid-1;
}else if(nums[mid]<target){
lo=mid+1;
}else return mid;
}
}*/
}
return -1;
}
1ms,99% 纯 if 判断** target 和 mid 的位置,然后选择移动 lo 还是 hi**,一开始我随便找了几组数然后就开始写,写到后面发现都是 bug😂,这里画个图很方便

在里面找点会很清晰
解法二
当然还有一种更加简单也不用这么复杂的方法
public static int search(int[] nums, int target) {
int lo=0,hi=nums.length-1;
if(nums==null||nums.length<=0){
return -1;
}
int index=-1;
while(lo<=hi){
int mid=lo+(hi-lo)/2;
if(nums[mid]>=nums[lo]){
//左半部分有序
index=binarySearch(nums,target,lo,mid);
//对右半部分二分
if(index==-1){
lo=mid+1;
//lo-->mid 没找到就对右半部分继续划分
} else return index;
} else if(nums[mid]<nums[lo]){
//右半部分有序
index=binarySearch(nums,target,mid,hi);
if(index==-1){
hi=mid-1;
} else return index;
}
}
return index;
}
public static int binarySearch(int []nums,int target,int lo,int hi){
while(lo<=hi){
int mid=lo+(hi-lo)/2;
if(nums[mid]>target){
hi=mid-1;
} else if(nums[mid]<target){
lo=mid+1;
} else return mid;
}
return -1;
}
这个应该比上一个慢一点,最好情况下是O(logN)直接将** target **划分到有序的那一边,如果没划分到有序的那一边就会花费时间去二分尝试切割数组,时间复杂度应该是logN+log(N/2)+log(N/4)+...log(N/N) 最后整体复杂度应该是O(logN*logN) ,虽然比 logN 好很多,但是并不是我们想要的算法
解法三
相当巧妙的解法!参考 lcus,通过判断 target和mid的位置,如果target和mid不在同一段就将 【4,5,6,7,0,1,2】 转换成 【4,5,6,7,INT_MAX,INT_MAX,INT_MAX】或者【INT_MIN,INT_MIN,INT_MIN,INT_MIN,0,1,2】 然后再进行二分
class Solution {
public int search(int[] nums, int target) {
if(nums==null || nums.length<=0) return -1;
int left=0,right=nums.length-1;
while(left<right){
int mid=left+(right-left)/2;
//这一步 (nums[mid]>=nums[0])==(target>=nums[0]) 很巧秒,其实用异或也可以
int midNum=(nums[mid]>=nums[0])==(target>=nums[0])?nums[mid]:
nums[mid]>=nums[0]?Integer.MIN_VALUE:Integer.MAX_VALUE;
if(midNum<target){
left=mid+1;
}else{
right=mid;
}
}
return nums[left]!=target?-1:left;
}
}
(nums[mid]>=nums[0])==(target>=nums[0]) 这一步很巧妙,满足这个关系就说明 mid 和 target 在同一段,不用变化,可以直接求,否则就根据 mid 的位置考虑如何变化
81. 搜索旋转排序数组 II
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,0,1,2,2,5,6] 可能变为 [2,5,6,0,0,1,2] )。
编写一个函数来判断给定的目标值是否存在于数组中。若存在返回 true,否则返回 false。
示例 1:
输入:nums = [2,5,6,0,0,1,2], target = 0
输出:true
示例 2:
输入:nums = [2,5,6,0,0,1,2], target = 3
输出:false
进阶:
- 这是 搜索旋转排序数组 的延伸题目,本题中的
nums可能包含重复元素。 - 这会影响到程序的时间复杂度吗?会有怎样的影响,为什么?
解法一
WA 哭了,好难搞,要是在工程上我肯定直接遍历了,太细节了这波
func search(nums []int, target int) bool {
n:=len(nums)
if n==0{
return false
}
left:=0
right:=n-1
for left<right {
mid:=left+(right-left)/2+1
if nums[mid]>nums[right] { //左半边
//target 在 [left,mid) 的有序区间内
if nums[left]<=target && target<nums[mid]{
right=mid-1
}else{
left=mid
}
}else if nums[mid]<nums[right]{
//target 在 [mid,right]
if nums[mid]<=target && target<=nums[right]{
left=mid
}else{
right=mid-1
}
}else{
//mid==right 看 right 是不是 target
if nums[right]==target{
return true
}
right--
}
}
return nums[left]==target
}
看着别人的题解写都 WA 了 5,6 次。这个其实就不能按照上一题的思路来了,因为有重复的,不好判断 mid 和 target 是不是在同一边
解法二
(update:2020/4/8)和上面的搜索最小值一样,如果只是中间重复没有任何影响,但是如果是头尾重复,那么问题就大了,我们就没办法通过头或者尾的值,判断 target 和 mid 所在的区间,所以我们可以开始先对头尾去重,这样就可以方便判断 target 和 mid 所在区间,比如 1 0 1 1 1 就可以变成 1 0,然后再进行二分就很简单了
class Solution:
def search(self, nums: List[int], target: int) -> bool:
left, right = 0, len(nums)-1
res = 0
# 尾部去重,方便确定 target 和 mid 所在区间
while right >= 0 and nums[right] == nums[0]:
right -= 1
while left <= right:
mid = left + (right-left)//2
v = nums[mid] if (nums[mid] < nums[0]) == (target < nums[0]) else float("inf") if nums[mid] < nums[0] else float("-inf")
if v <= target:
res = mid
left = mid + 1
else:
right = mid - 1
return True if nums[res] == target else False
744. 寻找比目标字母大的最小字母
给你一个排序后的字符列表 letters ,列表中只包含小写英文字母。另给出一个目标字母 target,请你寻找在这一有序列表里比目标字母大的最小字母。
在比较时,字母是依序循环出现的。举个例子:
- 如果目标字母
target = 'z'并且字符列表为letters = ['a', 'b'],则答案返回'a'
示例:
输入:
letters = ["c", "f", "j"]
target = "a"
输出:"c"
输入:
letters = ["c", "f", "j"]
target = "c"
输出:"f"
输入:
letters = ["c", "f", "j"]
target = "d"
输出:"f"
输入:
letters = ["c", "f", "j"]
target = "g"
输出:"j"
输入:
letters = ["c", "f", "j"]
target = "j"
输出:"c"
输入:
letters = ["c", "f", "j"]
target = "k"
输出:"c"
提示:
letters长度范围在[2, 10000]区间内。letters仅由小写字母组成,最少包含两个不同的字母。- 目标字母
target是一个小写字母。
解法一
按照新模板写的,题解区很多人讨论['z','a','b']这样的 case,其实我觉得没必要,纠结这没啥意义,可能还是题目描述有点问题,我们就直接当普通二分写就行了
public char nextGreatestLetter(char[] letters, char target) {
int left=0,right=letters.length-1;
int res=0; //注意找不到的情况
while(left<=right){
int mid=(left+right)/2;
if(letters[mid]>target){
res=mid;
right=mid-1;
}else{
left=mid+1;
}
}
return letters[res];
}
34. 在排序数组中查找元素的第一个和最后一个位置
给定一个按照升序排列的整数数组 nums,和一个目标值 target。找出给定目标值在数组中的开始位置和结束位置。
你的算法时间复杂度必须是 O(log n) 级别。
如果数组中不存在目标值,返回 [-1, -1]。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
解法一
时间复杂度 O(logN),肯定还是要二分
//两次二分
public int[] searchRange(int[] nums, int target) {
if(nums.length<=0){
return new int[]{-1,-1};
}
return new int[]{left(nums,target,0,nums.length-1),right(nums,target,0,nums.length-1)};
}
//5,7,7,8,8,8,8,10,10
public int left(int []nums,int target,int lo,int hi){
while(lo<=hi){
int mid=lo+(hi-lo)/2;
//System.out.println("lo: "+nums[lo]+"mid: "+nums[mid] +"hi: "+nums[hi]);
if(nums[mid]<target){
lo=mid+1;
}else if(nums[mid]>target){
hi=mid-1;
}else if(mid>0){ //nums[mid]=target
if(nums[mid-1]!=target){
return mid;
}else{
//控制向左找
hi=mid-1;
}
}else{
return mid; //0
}
}
return -1;
}
public int right(int []nums,int target,int lo,int hi){
while(lo<=hi){
int mid=lo+(hi-lo)/2;
if(nums[mid]<target){
lo=mid+1;
}else if(nums[mid]>target){
hi=mid-1;
}else if(mid<nums.length-1){
if(nums[mid+1]!=target){
return mid;
}else{
//控制向右找
lo=mid+1;
}
}else{
return mid; //nums.length
}
}
return -1;
}
1ms ,99% 核心就是两次二分,分别向左和向后二分整个数组, 在相等的时候并不返回,多判断一下,左边的就控制 hi 向左边继续找,右边就控制 lo 向右边继续找,直到下一个不等于 target 就返回,和上面一题一样都是二分的变种
解法二
统一的解法,上面的做法虽然直白,但是没有通用性,这里借鉴评论区大佬 liweiwei1419 的 讲解 写一个通用的解法,之前写二分一直都是凭感觉,不注意细节,有错误就 debug,东改一改,西改一改,然后就过了。毫无章法,以后要统一写法了
//两次二分
public int[] searchRange(int[] nums, int target) {
if(nums.length<=0){
return new int[]{-1,-1};
}
return new int[]{left(nums,target,0,nums.length-1),right(nums,target,0,nums.length-1)};
}
//找大于等于 target 的第一个元素,小于肯定不符合
public int left(int []nums,int target,int lo,int hi){
while(lo<hi){
int mid=lo+(hi-lo)/2;
if(nums[mid]<target){ //排除小于 target 的,剩下【lo,hi】都是大于等于的
lo=mid+1;
}else{
hi=mid;
}
}
return nums[hi]==target?hi:-1;
}
//找小于等于 target 的最后一个元素,大于肯定不符合
public int right(int []nums,int target,int lo,int hi){
while(lo<hi){
//选取右中值
int mid=lo+(hi-lo)/2+1;
if(nums[mid]>target){ //排除大于 target, 剩下 [lo,hi] 都是小于等于的
hi=mid-1;
}else{
//根据这个判断需要选取右中值
lo=mid;
}
}
return nums[hi]==target?hi:-1;
}
新模板
新模板比较好写
public int[] searchRange(int[] nums, int target) {
if(nums==null || nums.length<=0) return new int[]{-1,-1};
return new int[]{leftSearch(nums,target),rightSearch(nums,target)};
}
public int leftSearch(int[] nums,int target){
int left=0,right=nums.length-1;
int res=right;
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]>=target){
res=mid;
right=mid-1;
}else{
left=mid+1;
}
}
return nums[res]==target?res:-1;
}
public int rightSearch(int[] nums,int target){
int left=0,right=nums.length-1;
int res=left;
while(left<=right){
int mid=left+(right-left)/2;
if(nums[mid]<=target){
res=mid;
left=mid+1;
}else{
right=mid-1;
}
}
return nums[res]==target?res:-1;
}
面试题 53 - II. 0~n-1 中缺失的数字
一个长度为 n-1 n 的递增排序数组中的所有数字都是唯一的,并且每个数字都在范围0~n-1 0~n 之内。在范围0~n-1 0~n 内的n n+1 个数字中有且只有一个数字不在该数组中,请找出这个数字。
示例 1:
输入:[0,1,3]
输出:2
示例 2:
输入:[0,1,2,3,4,5,6,7,9]
输出:8
限制:
1 <= 数组长度 <= 10000
解法一
这题的题目描述感觉有点问题我稍微改了下
public int missingNumber(int[] nums) {
int left=0,right=nums.length-1;
while(left<right){
int mid=left+(right-left)/2;
if(nums[mid]==mid){
left=mid+1;
}else{
right=mid;
}
}
if(nums[left]==left) return left+1; //只有一个数
return left;
}
二分找那个索引不对的元素就 ok 了,按照模板写的,排除法,排除相等的,最后返回的索引left就是缺失的数字
852. 山脉数组的峰顶索引
我们把符合下列属性的数组 A 称作山脉:
- A.length >= 3
- 存在 0 < i < A.length - 1 使得 A[0] < A[1] < … A[i-1] < A[i] > A[i+1] > … > A[A.length - 1]
给定一个确定为山脉的数组,返回任何满足 A[0] < A[1] < ... A[i-1] < A[i] > A[i+1] > ... > A[A.length - 1] 的 i 的值。
示例 1:
输入:[0,1,0]
输出:1
示例 2:
输入:[0,2,1,0]
输出:1
解法一
其实还是上面的模板,只不过做了一点点改动而已,很傻逼的 WA 了一发,我也是服了自己了
public static int peakIndexInMountainArray(int[] A) {
int left=0,right=A.length-1;
while(left<right){
int mid=left+(right-left)/2;
//System.out.println(mid);
if (mid>0 && mid<A.length && A[mid] > A[mid-1] && A[mid]<A[mid+1]) {
left=mid+1;
}else if (mid>0 && mid<A.length && A[mid]< A[mid-1] && A[mid]>A[mid+1]){
right=mid-1;
}else{
return mid;
}
}
return left;
}
代码优化 2020.4.9 不知道为啥之前写成哪个鬼样子。
public static int peakIndexInMountainArray(int[] A) {
int left=0,right=A.length-1;
while(left<right){
int mid=left+(right-left)/2;
if (A[mid]<A[mid+1]) {
left=mid+1;
}else{
right=mid;
}
}
return left;
}
1095. 山脉数组中查找目标值
(这是一个 交互式问题 )
给你一个 山脉数组 mountainArr,请你返回能够使得 mountainArr.get(index) 等于 target 最小 的下标 index 值。
如果不存在这样的下标 index,就请返回 -1。
何为山脉数组?如果数组 A 是一个山脉数组的话,那它满足如下条件:
首先,A.length >= 3
其次,在 0 < i < A.length - 1 条件下,存在 i 使得:
A[0] < A[1] < ... A[i-1] < A[i]A[i] > A[i+1] > ... > A[A.length - 1]
你将 不能直接访问该山脉数组,必须通过 MountainArray 接口来获取数据:
MountainArray.get(k)- 会返回数组中索引为k的元素(下标从 0 开始)MountainArray.length()- 会返回该数组的长度
注意:
对 MountainArray.get 发起超过 100 次调用的提交将被视为错误答案。此外,任何试图规避判题系统的解决方案都将会导致比赛资格被取消。
为了帮助大家更好地理解交互式问题,我们准备了一个样例 “答案”:https://leetcode-cn.com/playground/RKhe3ave,请注意这 不是一个正确答案。
示例 1:
输入:array = [1,2,3,4,5,3,1], target = 3
输出:2
解释:3 在数组中出现了两次,下标分别为 2 和 5,我们返回最小的下标 2。
示例 2:
输入:array = [0,1,2,4,2,1], target = 3
输出:-1
解释:3 在数组中没有出现,返回 -1。
提示:
3 <= mountain_arr.length() <= 100000 <= target <= 10^90 <= mountain_arr.get(index) <= 10^9
解法一
这题,咋说呢,数据太弱了,配不上 hard 题,顶多算个 mid 偏简单,数据大的时候可以考虑加上缓存,这样就比较有意思了,这里我就懒得加了😁
func findInMountainArray(target int, mountainArr *MountainArray) int {
n := mountainArr.length()
//寻找山顶
left := 0
right := n - 1
for left < right {
mid := left + (right-left)/2
//mid+1 肯定不会越界
if mountainArr.get(mid) < mountainArr.get(mid+1) {
left = mid + 1
} else {
right = mid
}
}
res := -1
res = binarySearchUp(mountainArr, target, 0, left)
if res == -1 {
res = binarySearchDown(mountainArr, target, left, n-1)
}
return res
}
func binarySearchUp(mountainArr *MountainArray, target, left, right int) int {
for left < right {
mid := left + (right-left)/2
if mountainArr.get(mid) < target {
left = mid + 1
} else {
right = mid
}
}
if mountainArr.get(left) == target {
return left
}
return -1
}
func binarySearchDown(mountainArr *MountainArray, target, left, right int) int {
for left < right {
mid := left + (right-left)/2
if mountainArr.get(mid) > target {
left = mid + 1
} else {
right = mid
}
}
if mountainArr.get(left) == target {
return left
}
return -1
}
这两个二分是可以合并的,懒得合了(太懒了吧你也😅)
UPDATE: 2020.7.14
自定义函数传递,简化代码
func findInMountainArray(target int, mA *MountainArray) int {
var n = mA.length()
var left = 0
var right = n-1
var maxIdx = right
for left <= right{
mid := left + (right-left)/2
//左中,所以 mid+1 不会越界
if mA.get(mid) > mA.get(mid+1){
maxIdx = mid
right = mid - 1
}else{
left = mid + 1
}
}
lr := search(mA, target, 0, maxIdx, func(i int, j int)bool{
return i <= j
})
if lr != -1{
return lr
}
return search(mA, target, maxIdx+1, n-1, func(i int, j int)bool{
return i >= j
})
}
func search(mA *MountainArray, target int, left int, right int, less func(int, int)bool) int {
var res = left
for left <= right{
mid := left + (right-left)/2
if less(mA.get(mid), target){
res = mid
left = mid + 1
}else{
right = mid - 1
}
}
if mA.get(res) != target{
return -1
}
return res
}
162. 寻找峰值
峰值元素是指其值大于左右相邻值的元素。
给定一个输入数组 nums,其中 nums[i] ≠ nums[i+1],找到峰值元素并返回其索引。
数组可能包含多个峰值,在这种情况下,返回任何一个峰值所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;
或者返回索引 5, 其峰值元素为 6。
说明:
你的解法应该是 O(logN) 时间复杂度的。
解法一
题目挑明了 logN 的复杂度,那么肯定就是二分了,那是怎么个二分的思路呢?题目其实也说了很清楚了,边界的左右两边都是-∞ 所以我们直接按照递增的去搜,最后肯定能搜索到峰值
public int findPeakElement(int[] nums) {
int left=0,right=nums.length-1;
while(left<right){
int mid=left+(right-left)/2;
if(/*mid+1<nums.length &&*/nums[mid]<nums[mid+1]){
left=mid+1;
}else{
right=mid;
}
}
return left;
}
liweiwei 大佬的二分模板真好用!!!
74. 搜索二维矩阵
编写一个高效的算法来判断 m x n 矩阵中,是否存在一个目标值。该矩阵具有如下特性:
每行中的整数从左到右按升序排列。 每行的第一个整数大于前一行的最后一个整数。 示例 1:
输入:
matrix = [
[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 50]
]
target = 3
输出:true
示例 2:
输入:
matrix = [
[1, 3, 5, 7],
[10, 11, 16, 20],
[23, 30, 34, 50]
]
target = 13
输出:false
解法一
public boolean searchMatrix(int[][] matrix, int target) {
if(matrix==null || matrix.length<=0 || matrix[0].length<=0){
return false;
}
int m=matrix.length;
int n=matrix[0].length;
int low=0,high=m-1;
if (target>matrix[m-1][n-1] || target < matrix[0][0]) {
return false;
}
while(low<=high){ //二分确定在哪一行
int mid=low+(high-low)/2;
if (target == matrix[mid][0]) {
return true;
}else if(matrix[mid][0]<target){
low=mid+1;
}else{
high=mid-1;
}
}
int column=low!=0?low-1:low;
low=0;
high=n-1;
while(low<high){
int mid=low+(high-low)/2;
if (matrix[column][mid]==target) {
return true;
}else if(matrix[column][mid] < target){
low=mid+1;
}else{
high=mid-1;
}
}
return target==matrix[column][low];
}
😔,这题 wa 了 11 次,是的,11 次,可想而知我有多彩,最后写出来的解法还是如此的难看,主要就是在确定在哪一行的时候写出了好多问题,可以看到我上下的两种二分方法是不一样的,前期就揪着一种写,按照上面的板子写,结果写出了一堆 bug… 以后写二分还是要注意啊,1s 确定思路,代码写了 3h。
解法二
看了评论区写出来的,利用取模和除将二维数组拉成一维的,相当的优秀,也不用考虑那些边界,时间复杂度和上面一样log(nm)
public boolean searchMatrix(int[][] matrix, int target) {
if(matrix==null || matrix.length<=0 || matrix[0].length<=0){
return false;
}
int m=matrix.length;
int n=matrix[0].length;
int left=0,right=m*n-1;
while(left<right){
int mid=left+(right-left)/2;
if(matrix[mid/n][mid%n]<target){
left=mid+1;
}else{
right=mid;
}
}
return matrix[left/n][left%n]==target;
}
240. 搜索二维矩阵 II
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例: 现有矩阵 matrix 如下:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
给定 target = 5,返回 true。
给定 target = 20,返回 false。
解法一
看上一题 240. 搜索二维矩阵 的评论区的时候看到了这种解法
public boolean searchMatrix(int[][] matrix, int target) {
if(matrix==null || matrix.length<=0 || matrix[0].length<=0){
return false;
}
int m=matrix.length;
int n=matrix[0].length;
int column=0,row=m-1;
while(column<n && row>=0){
//System.out.println(row+","+column);
if (matrix[row][column]==target) {
return true;
}
if (matrix[row][column] > target) {
row--;
}else{
column++;
}
}
return false;
}
整个矩阵从左上到右下,其实就分为了两块,每个元素的左上一定小于当前元素,右下一定大于当前元素,这题也可以二分,就像下面的 1351. 统计有序矩阵中的负数一样,但是时间复杂度会高一些
1351. 统计有序矩阵中的负数
Difficulty: 简单
给你一个 m * n 的矩阵 grid,矩阵中的元素无论是按行还是按列,都以非递增顺序排列。
请你统计并返回 grid 中 负数 的数目。
示例 1:
输入:grid = [[4,3,2,-1],[3,2,1,-1],[1,1,-1,-2],[-1,-1,-2,-3]]
输出:8
解释:矩阵中共有 8 个负数。
示例 2:
输入:grid = [[3,2],[1,0]]
输出:0
示例 3:
输入:grid = [[1,-1],[-1,-1]]
输出:3
示例 4:
输入:grid = [[-1]]
输出:1
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 100-100 <= grid[i][j] <= 100
解法一
没啥好说的,和上面的解法一样,从左下角向上搜索
func countNegatives(grid [][]int) int {
if len(grid) <= 0 {
return 0
}
var m, n = len(grid), len(grid[0])
var count = 0
var i, j = m-1, 0
for i >= 0 && j < n {
if grid[i][j] < 0 {
count += n - j
i--
}else{
j++
}
}
return count;
}
解法二
O(mlogn) 解法
//O(mlogn) 只利用了行逆序的条件
func countNegatives(grid [][]int) int {
if len(grid) <= 0 {
return 0
}
var count = 0
var m = len(grid)
var n = len(grid[0])
for i := 0; i < m; i++ {
count += (n - search(grid[i]))
}
return count
}
func search(nums []int) int {
var left = 0
var right = len(nums)-1
var res = right+1
for left <= right {
mid := left + (right-left)/2
if nums[mid] < 0 {
res = mid
right = mid - 1
}else{
left = mid + 1
}
}
return res
}
4. 寻找两个有序数组的中位数
给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。
请你找出这两个有序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。
示例 1:
nums1 = [1, 3]
nums2 = [2]
则中位数是 2.0
示例 2:
nums1 = [1, 2]
nums2 = [3, 4]
则中位数是 (2 + 3)/2 = 2.5
解法一
Hard 题,首先想到的是归并,但是时间复杂度不符合要求,最低要求 O(log(m+n)),想了好一会儿实在是想不出来(菜)然后看了评论区的解法
//find nums1+nums2 /2 大的数
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int m=nums1.length;
int n=nums2.length;
int leftMid=(m+n+1)/2;
int rightMid=(m+n+2)/2;
return (findMedian(nums1,0,m-1,nums2,0,n-1,leftMid) + findMedian(nums1,0,m-1,nums2,0,n-1,rightMid)) * 0.5;
}
// i
//1 2 3 5
// j
//1 2 4 6 7 8 9 k=6 find k/2=3
//
// i
//*1 2 3* 5
// j
//1 2 4 6 7 8 9 k=3 find k/2=1 res=4
public double findMedian(int[] nums1,int left1,int right1, int[] nums2,int left2,int right2,int k) {
int len1=right1-left1+1;
int len2=right2-left2+1;
if (len1==0) {
return nums2[left2+k-1];
}
if (len2==0) {
return nums1[left1+k-1];
}
if (k==1) {
return Math.min(nums1[left1],nums2[left2]);
}
int i=left1+Math.min(len1,k/2)-1;
int j=left2+Math.min(len2,k/2)-1;
if (nums1[i] < nums2[j]) {
return findMedian(nums1,i+1,right1,nums2,left2,right2,k-(i-left1+1));
}else{
return findMedian(nums1,left1,right1,nums2,j+1,right2,k-(j-left2+1));
}
}
这种解法还是挺妙的,求第 k 小的思路,两个数组都是有序的,我们要求第 k 小,我们可以将 k 一分为二,看看两个数组的 k/2 位置的元素哪个大哪个小,小的哪个数组前 k/2 个元素就可以直接排除掉,因为他们必不可能是第 k 小的元素,举个例子就很容易理解
1 2 3 5
1 2 4 6 7 8 9 k=6
k/2=3, 分别在两数组中找第三个元素,也即是 3,4 明显 3 比较小,所以我们可以直接排除第一个数组的 1,2,3 三个元素,他们必不可能是第 k 小的元素!
*1 2 3* 5
1 2 4 6 7 8 9 k=3
然后重复上面的过程,每次排除k/2 的元素,最后在log(k) 的时间复杂度下就能找到两个数组的 mid,而这里k=(m+n+1)/2 所以是符合题目要求的,除此之外,我们还需要考虑奇数和偶数的情况,那我们就可以分别计算一下,我们求一下左中位数和右中位数,如果是奇数左中和右中就是同一个(k)/2==(k+1)/2 ,偶数的话就是(k)/2和(k+1)/2分别就是左中和右中,然后我们直接/2 就得到了解
658. 找到 K 个最接近的元素
给定一个排序好的数组,两个整数 k 和 x,从数组中找到最靠近 x(两数之差最小)的 k 个数。返回的结果必须要是按升序排好的。如果有两个数与 x 的差值一样,优先选择数值较小的那个数。
示例 1:
输入:[1,2,3,4,5], k=4, x=3
输出:[1,2,3,4]
示例 2:
输入:[1,2,3,4,5], k=4, x=-1
输出:[1,2,3,4]
说明:
- k 的值为正数,且总是小于给定排序数组的长度。
- 数组不为空,且长度不超过 104
- 数组里的每个元素与 x 的绝对值不超过 104
解法一
双指针,少点套路,多点真诚
public List<Integer> findClosestElements(int[] arr, int k, int x) {
int left=0,right=arr.length-1;
int count=0;
while(left<right){
if(Math.abs(arr[left]-x)<=Math.abs(arr[right]-x)){
right--;
}else{
left++;
}
count++;
if(count==arr.length-k) break;
}
List<Integer> res=new ArrayList<>();
for(int i=left;i<=right;i++) res.add(arr[i]);
return res;
}
解法二
二分的解法,有点 trick,不容易想到,参考 题解
public List<Integer> findClosestElements(int[] arr, int k, int x) {
//左边界的取值范围
int left=0,right=arr.length-k;
while(left<right){
int mid=left+(right-left)/2;
if(x-arr[mid]>arr[mid+k]-x){
left=mid+1;
}else{
right=mid;
}
}
List<Integer> res=new ArrayList<>();
for(int i=left;i<left+k;i++) res.add(arr[i]);
return res;
}
367. 有效的完全平方数
Difficulty: 简单
给定一个正整数 num,编写一个函数,如果 num 是一个完全平方数,则返回 True,否则返回 False。
**说明:**不要使用任何内置的库函数,如 sqrt。
示例 1:
输入:16
输出:True
示例 2:
输入:14
输出:False
解法一
二分
func isPerfectSquare(num int) bool {
var left = 0
var right = num
var res = num + 1
for left <= right {
mid := left + (right-left)/2
if mid*mid >= num {
res = mid
right = mid - 1
} else {
left = mid + 1
}
}
return res*res == num
}
解法二
完全平方数的性质
//完全平方数性质 n^2 = 1 + 3 + 5 +...+2n+1 (前 n 个奇数的和)
//所以只需要判断 num 能不能被奇数减成 0 就行了
func isPerfectSquare(num int) bool {
var i = 1
for num > 0 {
num -= i
i += 2
}
return num == 0
}
475. 供暖器
Difficulty: 简单
冬季已经来临。 你的任务是设计一个有固定加热半径的供暖器向所有房屋供暖。
现在,给出位于一条水平线上的房屋和供暖器的位置,找到可以覆盖所有房屋的最小加热半径。
所以,你的输入将会是房屋和供暖器的位置。你将输出供暖器的最小加热半径。
说明:
- 给出的房屋和供暖器的数目是非负数且不会超过 25000。
- 给出的房屋和供暖器的位置均是非负数且不会超过 10^9。
- 只要房屋位于供暖器的半径内(包括在边缘上),它就可以得到供暖。
- 所有供暖器都遵循你的半径标准,加热的半径也一样。
示例 1:
输入:[1,2,3],[2]
输出:1
解释:仅在位置 2 上有一个供暖器。如果我们将加热半径设为 1,那么所有房屋就都能得到供暖。
示例 2:
输入:[1,2,3,4],[1,4]
输出:1
解释:在位置 1, 4 上有两个供暖器。我们需要将加热半径设为 1,这样所有房屋就都能得到供暖。
解法一
这个题目感觉不是 easy 啊,一开始想劈叉了,以为是二分答案,写了半天后来 WA 在一个很大的 case,一直以为是溢出了,改了半天的 bug 没改出来。后来自己按照 case 的规律构建了一个小的 case,发现也 WA 了,然后才意识到是方法错了,(case: [4,9] [4,8]),这个 case 按照二分答案的思路就是错的,二分答案是思路就是验证该半径下能否覆盖整个区间,其实也是题目理解有点问题,题目的要求是覆盖每个房子,而不是覆盖整个区间,所以只需要找到每个房子最近的供暖器就行了,然后统计这些最小值得最大值就是我们需要的半径
func findRadius(houses []int, heaters []int) int {
//边界处理
heaters = append(heaters, math.MaxInt32)
heaters = append(heaters, math.MinInt32)
sort.Ints(heaters)
var Min = func (a, b int) int { if a < b {return a}; return b}
var Max = func (a, b int) int { if a < b {return b}; return a}
var res = 0
for _, h := range houses{
left := search(heaters, h)
res = Max(res, Min(h-heaters[left], heaters[left+1]-h))
}
return res
}
//target 左边最近的一个
func search(heaters []int, target int) int {
var left, right = 0, len(heaters)-1
var res = left //左边没有供暖器
for left <= right {
mid := left + (right-left)/2
if heaters[mid] <= target{
res = mid
left = mid + 1
}else{
right = mid - 1
}
}
return res
}
另一种写法,不额外处理边界,也是一开始的写法
func findRadius(houses []int, heaters []int) int {
sort.Ints(heaters)
var n = len(heaters)
var Min = func (a, b int) int { if a < b {return a}; return b}
var Max = func (a, b int) int { if a < b {return b}; return a}
var res = 0
for _, h := range houses{
left := search(heaters, h)
if left == -1{ //全部大于 hourse, 取最小的那个
res = Max(res, heaters[0]-h)
}else if left+1 < n{
res = Max(res, Min(h-heaters[left], heaters[left+1]-h))
}else{
res = Max(res, h-heaters[left])
}
}
return res
}
//target 左边最近的一个
func search(heaters []int, target int) int {
var left, right = 0, len(heaters)-1
var res = -1 //左边没有供暖器
for left <= right {
mid := left + (right-left)/2
if heaters[mid] <= target{
res = mid
left = mid + 1
}else{
right = mid - 1
}
}
return res
}
时间复杂度细看的话应该是 O(MlogM + MlogN)(M,N 分别代表 houses 和 heaters 的长度)
解法二
双指针,时间复杂度差别不大
func findRadius(houses []int, heaters []int) int {
heaters = append(heaters, math.MaxInt32)
heaters = append(heaters, math.MinInt32)
sort.Ints(heaters)
sort.Ints(houses)
var n = len(heaters)
var Min = func (a, b int) int { if a < b {return a}; return b}
var Max = func (a, b int) int { if a < b {return b}; return a}
var res = 0
var left = 0
for _, h := range houses {
for left < n && heaters[left] < h {
left++
}
res = Max(res, Min(heaters[left]-h, h-heaters[left-1]))
}
return res
}
时间复杂度细看的话应该是 O(NlogN + MlogM + N + M)(M,N 分别代表 houses 和 heaters 的长度),差别不大,不过很明显双指针的好写很多
二分答案
1283. 使结果不超过阈值的最小除数
给你一个整数数组 nums 和一个正整数 threshold ,你需要选择一个正整数作为除数,然后将数组里每个数都除以它,并对除法结果求和。
请你找出能够使上述结果小于等于阈值 threshold 的除数中 最小 的那个。
每个数除以除数后都向上取整,比方说 7/3 = 3 , 10/2 = 5 。
题目保证一定有解。
示例 1:
输入:nums = [1,2,5,9], threshold = 6
输出:5
解释:如果除数为 1 ,我们可以得到和为 17 (1+2+5+9)。
如果除数为 4 ,我们可以得到和为 7 (1+1+2+3) 。如果除数为 5 ,和为 5 (1+1+1+2)。
示例 2:
输入:nums = [2,3,5,7,11], threshold = 11
输出:3
示例 3:
输入:nums = [19], threshold = 5
输出:4
提示:
1 <= nums.length <= 5 * 10^41 <= nums[i] <= 10^6nums.length <= threshold <= 10^6
解法一
周赛的题,太蠢了,没做出来。
public int smallestDivisor(int[] nums, int threshold) {
int left=1,right=1000000;
while(left<right){
int mid=left+(right-left)/2;
int sum=0;
for (int i=0;i<nums.length;i++) {
sum+=(nums[i]+mid-1)/mid; //向上取整
}
if (sum>threshold) {
left=mid+1;
}else{
right=mid;
}
}
return left;
}
其实只要明确一点这题就很容易想到二分,解空间为:[1,max(nums[i])] 我们只需要在这个区间之内做二分搜索就 ok 了,再然后就是向上取整的一个小技巧
287. 寻找重复数
给定一个包含 n + 1 个整数的数组 nums,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。假设只有一个重复的整数,找出这个重复的数。
示例 1:
输入:[1,3,4,2,2]
输出:2
示例 2:
输入:[3,1,3,4,2]
输出:3
说明:
- 不能更改原数组(假设数组是只读的)。
- 只能使用额外的 O(1) 的空间。
- 时间复杂度小于 O(n2) 。
- 数组中只有一个重复的数字,但它可能不止重复出现一次
解法一
这题还是挺有意思的,题目要求了数组 nums 是只读的,且不能使用额外的空间,且时间复杂度还要小于 O(N^2),否则的话其实可以排序,或者使用 Hash 表来做,这里我们使用二分来做
//update: 2020.5.26 其实也属于二分答案
public int findDuplicate(int[] nums){
int left=1,right=nums.length-1;
//这里实际上是对【1,2,3,4,...n-1】这个区间进行二分
//在过程中对 mid 检测每个数在 nums 数组中出现的次数
//1 3 4 2 2 实际上是对【1,2,3,4】区间进行二分
while(left<right){
int mid=left+(right-left)/2+1;
//小于 mid 的数大于 mid, 排除 mid
if(count(nums,mid)>=mid){
right=mid-1;
}else{
left=mid;
}
}
return left;
}
//n-1 个整数 , 1~n 有 n 个数
//1 2 2 3 4 1~4 之间,1 2 3 4
public int count(int[] nums,int n){
int res=0;
for (int i=0;i<nums.length;i++) {
if (nums[i]<n) {
res++;
}
}
return res;
}
这样的解法还是很巧妙的,对 nums 数组的取值范围进行二分,二分的核心就是,nums 数组中,小于取值范围中 mid 的元素应该小于等于 mid
举个例子:[1 3 4 2 2] 取值范围是[1 2 3 4] ,取中点 2,正常情况下 nums 中小于等于 2 的元素,应该最多有 2 个,也就是[1 2]2 个,但是这里在 nums 中,有 3 个[1 2 2] 大于 2 了,这就说明一定有重复的元素,而且一定是小于中点 2 的,也就是在左半边,下一步就应该舍弃右半边,在[1,2]中继续查找
这里按照我们之前的模板来写,先找排除 mid 的条件,在 nums 中小于 mid 的元素的数量小于等于 mid 的时候,包括 mid 在内的右边界都会被排除,肯定都不是重复的元素 ,然后就按照模板写出二分就行了
解法二
快慢指针的做法,技巧性很强,一般人第一次做是很难想到这种做法的,其实和 链表专题 中的环形链表是一样的做法,然后按照那个思路走就行了,不清楚原理可以看看上面环形链表的解法
public int findDuplicate(int[] nums){
int slow=0,fast=0;
boolean isMeet=false;
while(true){
fast=isMeet?nums[fast]:nums[nums[fast]];
slow=nums[slow];
if (fast==slow) {
if (isMeet) {
return slow;
}
fast=0;
isMeet=true;
}
}
}
这种解法的关键是将数组值看作索引然后再数组像链表一样移动,比如 [1,2,3,4,5,6,7,8,9,5]用值作为索引连接起来就是1 2 3 4 [5 6 7 8 9] [5 6 7 8 9] .... ,时间复杂度O(N) 技巧性比较强,如果面试管不追问的话其实答出上面的二分就 ok 了
1011. 在 D 天内送达包裹的能力
传送带上的包裹必须在 D 天内从一个港口运送到另一个港口。
传送带上的第 i 个包裹的重量为 weights[i]。每一天,我们都会按给出重量的顺序往传送带上装载包裹。我们装载的重量不会超过船的最大运载重量。
返回能在 D 天内将传送带上的所有包裹送达的船的最低运载能力。
示例 1:
输入:weights = [1,2,3,4,5,6,7,8,9,10], D = 5
输出:15
解释:
船舶最低载重 15 就能够在 5 天内送达所有包裹,如下所示:
第 1 天:1, 2, 3, 4, 5
第 2 天:6, 7
第 3 天:8
第 4 天:9
第 5 天:10
请注意,货物必须按照给定的顺序装运,因此使用载重能力为 14 的船舶并将包装分成 (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) 是不允许的。
示例 2:
输入:weights = [3,2,2,4,1,4], D = 3
输出:6
解释:
船舶最低载重 6 就能够在 3 天内送达所有包裹,如下所示:
第 1 天:3, 2
第 2 天:2, 4
第 3 天:1, 4
示例 3:
输入:weights = [1,2,3,1,1], D = 4
输出:3
解释:
第 1 天:1
第 2 天:2
第 3 天:3
第 4 天:1, 1
提示:
1 <= D <= weights.length <= 500001 <= weights[i] <= 500
解法一
问题的解空间是单调的,所以可以直接二分答案,然后验证是否满足条件就可以了,时间复杂度O(NlogN)
public int shipWithinDays(int[] weights, int D) {
int sum=0,max=0;
for(int w:weights){
max=Math.max(w,max);
sum+=w;
}
int left=Math.max(sum/D,max),right=sum;
int res=0;
while(left<=right){
int mid=left+(right-left)/2;
if(check(weights,mid,D)){
res=mid;
right=mid-1;
}else{
left=mid+1;
}
}
return res;
}
//模拟判断
public boolean check(int[] weights,int load,int D){
int temp=0;
for(int w:weights){
if(temp+w>load){
temp=0;
D--;
}
temp+=w;
}
//return D>=0;
return D>0;
}
上面是用的一个 大佬 的模板,不是之前的模板,之前的模板我刚刚写了一发,写错了。
//之前的二分模板
public int shipWithinDays(int[] weights, int D) {
int sum=0,max=0;
for(int w:weights){
max=Math.max(w,max);
sum+=w;
}
int left=Math.max(sum/D,max),right=sum;
while(left<right){ //这里一开始写成<=了。...
int mid=left+(right-left)/2;
if(check(weights,mid,D)){
right=mid;
}else{
left=mid+1;
}
}
return left;
}
两种模板各有优点吧,这个大佬的模板相对更简单,但是 res 的初始值需要格外注意。
875. 爱吃香蕉的珂珂
珂珂喜欢吃香蕉。这里有 N 堆香蕉,第 i 堆中有 piles[i] 根香蕉。警卫已经离开了,将在 H 小时后回来。
珂珂可以决定她吃香蕉的速度 K (单位:根/小时)。每个小时,她将会选择一堆香蕉,从中吃掉 K 根。如果这堆香蕉少于 K 根,她将吃掉这堆的所有香蕉,然后这一小时内不会再吃更多的香蕉。
珂珂喜欢慢慢吃,但仍然想在警卫回来前吃掉所有的香蕉。
返回她可以在 H 小时内吃掉所有香蕉的最小速度 K(K 为整数)。
示例 1:
输入:piles = [3,6,7,11], H = 8
输出:4
示例 2:
输入:piles = [30,11,23,4,20], H = 5
输出:30
示例 3:
输入:piles = [30,11,23,4,20], H = 6
输出:23
提示:
1 <= piles.length <= 10^4piles.length <= H <= 10^91 <= piles[i] <= 10^9
解法一
一开始想用sum/H向上取整做左边界,结果直接爆掉了,case 还是很给力啊
//二分答案
public int minEatingSpeed(int[] piles, int H) {
int max=0;
for(int p:piles) max=Math.max(max,p);
int left=1,right=max;
int res=right;
while(left<=right){
int mid=left+(right-left)/2;
if(check(piles,mid,H)){
res=mid;
right=mid-1;
}else{
left=mid+1;
}
}
return res;
}
public boolean check(int[] piles,int k,int H){
int count=0;
for(int p:piles) count+=(p-1)/k+1; //向上取整
return count<=H;
}
1292. 元素和小于等于阈值的正方形的最大边长
给你一个大小为 m x n 的矩阵 mat 和一个整数阈值 threshold。
请你返回元素总和小于或等于阈值的正方形区域的最大边长;如果没有这样的正方形区域,则返回 0 。
示例 1:
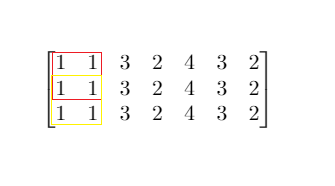
输入:mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
输出:2
解释:总和小于 4 的正方形的最大边长为 2,如图所示。
示例 2:
输入:mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
输出:0
示例 3:
输入:mat = [[1,1,1,1],[1,0,0,0],[1,0,0,0],[1,0,0,0]], threshold = 6
输出:3
示例 4:
输入:mat = [[18,70],[61,1],[25,85],[14,40],[11,96],[97,96],[63,45]], threshold = 40184
输出:2
提示:
1 <= m, n <= 300m == mat.lengthn == mat[i].length0 <= mat[i][j] <= 100000 <= threshold <= 10^5
解法一
这个题是个好题啊,又学到新东西了:二维前缀和,首先看到这道题就意识到了这是个二分答案的题,直接二分边长就行了,左端点1,右端点min(m,n),某个边长x满足的时候,大于x的都满足,某个x不满足的时候,小于x的都不满足,解空间具有单调性
所以关键问题就是check怎么写,如果直接暴力枚举所有矩形然后计算时间复杂度会很恐怖,这个时候就可以引入二维前缀和,我就不具体讲解了,看看 官方题解 就行了,写的挺好的
public int maxSideLength(int[][] mat, int threshold) {
int m=mat.length;
int n=mat[0].length;
int left=1,right=Math.min(m,n);
//核心公式
//sum([x1,y1]->[x2,y2])
//= P[x2][y2]-P[x2][y1-1]-P[x1-1][y2]+P[x1-1][y1-1]
//==> mat[i][j]=P[i][j]-P[i-1][j]-P[j-1][i]+P[i-1][j-1]
int[][] dp=new int[m+1][n+1];
for (int i=1;i<=m;i++) {
for (int j=1;j<=n;j++) {
dp[i][j]=mat[i-1][j-1]+dp[i-1][j]+dp[i][j-1]-dp[i-1][j-1];
}
}
int res=0;
while(left<=right){
int mid=left+(right-left)/2;
if(check(mat,mid,threshold,dp)){
res=mid;
left=mid+1;
}else{
right=mid-1;
}
}
return res;
}
public boolean check(int[][] mat,int side,int threshold,int[][] dp){
//枚举所有的左端点
for (int i=1;i+side-1<=mat.length;i++) {
for (int j=1;j+side-1<=mat[0].length;j++) {
int ri=i+side-1,rj=j+side-1;
//System.out.println(ri+","+rj+" dp:"+ dp[ri][rj]);
if(dp[ri][rj]-dp[i-1][rj]-dp[ri][j-1]+dp[i-1][j-1]<=threshold){
return true;
}
}
}
return false;
}
1300. 转变数组后最接近目标值的数组和
给你一个整数数组 arr 和一个目标值 target ,请你返回一个整数 value ,使得将数组中所有大于 value 的值变成 value 后,数组的和最接近 target (最接近表示两者之差的绝对值最小)。
如果有多种使得和最接近 target 的方案,请你返回这些整数中的最小值。
请注意,答案不一定是 arr 中的数字。
示例 1:
输入:arr = [4,9,3], target = 10
输出:3
解释:当选择 value 为 3 时,数组会变成 [3, 3, 3],和为 9 ,这是最接近 target 的方案。
示例 2:
输入:arr = [2,3,5], target = 10
输出:5
示例 3:
输入:arr = [60864,25176,27249,21296,20204], target = 56803
输出:11361
提示:
1 <= arr.length <= 10^41 <= arr[i], target <= 10^5
解法一
解空间在[0,max(arr)]上单调,所以可以二分答案
一开始傻傻的写了两个二分,一个找第一个小于等于 target 的,一个找大于等于的,其实根本就不用,这两个值肯定是连在一起的🤣
public int findBestValue(int[] arr, int target) {
int sum=0;
int left=0,right=Integer.MIN_VALUE;
for(int num:arr){
sum+=num;
right=Math.max(right,num);
}
if(sum<=target) return right;
int res=left;
while(left<=right){
int mid=left+(right-left)/2;
if(getSum(arr,mid)<=target){
res=mid;
left=mid+1;
}else{
right=mid-1;
}
}
//这两个值肯定是连在一起的
if(target-getSum(arr,res)<=getSum(arr,res+1)-target){
return res;
}
return res+1;
}
public int getSum(int[] arr,int mid){
int sum=0;
for(int a:arr){
sum+=a>mid?mid:a;
}
return sum;
}
LCP 12. 小张刷题计划
为了提高自己的代码能力,小张制定了 LeetCode 刷题计划,他选中了 LeetCode 题库中的 n 道题,编号从 0 到 n-1,并计划在 m 天内按照题目编号顺序刷完所有的题目(注意,小张不能用多天完成同一题)。
在小张刷题计划中,小张需要用 time[i] 的时间完成编号 i 的题目。此外,小张还可以使用场外求助功能,通过询问他的好朋友小杨题目的解法,可以省去该题的做题时间。为了防止“小张刷题计划”变成“小杨刷题计划”,小张每天最多使用一次求助。
我们定义 m 天中做题时间最多的一天耗时为 T(小杨完成的题目不计入做题总时间)。请你帮小张求出最小的 T是多少。
示例 1:
输入:
time = [1,2,3,3], m = 2输出:
3解释:第一天小张完成前三题,其中第三题找小杨帮忙;第二天完成第四题,并且找小杨帮忙。这样做题时间最多的一天花费了 3 的时间,并且这个值是最小的。
示例 2:
输入:
time = [999,999,999], m = 4输出:
0解释:在前三天中,小张每天求助小杨一次,这样他可以在三天内完成所有的题目并不花任何时间。
限制:
1 <= time.length <= 10^51 <= time[i] <= 100001 <= m <= 1000
解法一
知道是二分答案但是 check 写了好久没写出来,真菜啊
public int minTime(int[] time, int m) {
int left=0,right=0;//上界最多 sum(time)
for(int i=0;i<time.length;i++){
right+=time[i];
}
int res=right+1;
while(left<=right){
int mid=left+(right-left)/2;
if(check(time,mid,m)){
res=mid;
right=mid-1;
}else{
left=mid+1;
}
}
//其实返回 left 就行了,主要是避免搞混
return res;
}
//核心的 check
public boolean check(int[] time,int T,int m){
int day=1,sum=0,maxt=0;
for (int t:time) {
sum+=t;
maxt=Math.max(maxt,t); //维护每一组的最大值
if(sum-maxt>T){ //当前组减去最大值不满足
day++;
sum=t;
maxt=t;
}
}
return day<=m;
}
410. 分割数组的最大值
给定一个非负整数数组和一个整数 m,你需要将这个数组分成 m 个非空的连续子数组。设计一个算法使得这 m 个子数组各自和的最大值最小。
注意: 数组长度 n 满足以下条件:
- 1 ≤ n ≤ 1000
- 1 ≤ m ≤ min(50, n)
示例:
输入:
nums = [7,2,5,10,8]
m = 2
输出:
18
解释:
一共有四种方法将 nums 分割为 2 个子数组。
其中最好的方式是将其分为 [7,2,5] 和 [10,8],
因为此时这两个子数组各自的和的最大值为 18,在所有情况中最小。
解法一
Hard 题,但是感觉和前面的 mid 差不多,没啥好说的,个人感觉这题还没上面的 LCP12. 小张刷题计划 难,不过有个 case 挺恶心,算的 sum 会溢出,害我 WA 了一次,但是他结果返回的又是个 int,这就很蠢
//一样的套路
public int splitArray(int[] nums, int m) {
long left=0,right=0;
for(int num:nums){
left=Math.max(left,num);
right+=num;
}
long res=0;
while(left<=right){
long mid=left+(right-left)/2;
if(check(nums,mid,m)){
res=mid;
right=mid-1;
}else{
left=mid+1;
}
}
return (int)res;
}
//分为 m 组能否保证每组都小于等于 mid(如果可以说明还可以更小)
public boolean check(int[] nums,long limit,int m){
long sum=0;
int count=1;
for(int num:nums){
if(sum+num>limit){
sum=0;
count++;
}
sum+=num;
}
return count<=m;
}
NC82. 分组
题目描述 牛牛有一个 n 个数字的序列 a1,a2,a3…an 现在牛牛想把这个序列分成 k 段连续段,牛牛想知道分出来的 k 个连续段的段内数字和的最小值最大可以是多少?
示例 1
输入 : 4,2,[1,2,1,5]
输出 : 4
说明:
有 3 种分法
[1],[2,1,5],数字和分别为 1,8,最小值为 1
[1,2][1,5],数字和分别为 3,6,最小值为 3
[1,2,1],[5] 数字和分别为 4,5,最小值为 4
则最小值的最大值为 4
备注:
- 1 <= k <= n <= 1e5
- 0 <= ai <= 1e4
第一个参数整数 n 代表序列数字个数, 第二个参数整数 k 代表分出的段数, 第三个参数 vector a 包含 n 个元素代表 n 个数字
解法一
我是真的菜啊,上面一题会写这题就不会写了,果然我这种菜鸡刷题就是背题,变一下就不会了。其实和上面的正好是反过来的,上面是要最大值最小,这里是要最小值最大,所以 check 的思路也是相反的,上面是验证:分为 k 组能否保证每组都小于等于 mid。所以这题很显然就应该是:分为 k 组能否保证每组都大于等于 mid(这里验证也是逐渐逼近答案)
//最小值最大
public int solve (int n, int k, int[] a) {
int left = 0;
int right = 0;
for (int i = 0; i < a.length; i++) {
left = Math.min(left, a[i]);
right += a[i];
}
int res = 0;
while (left <= right) {
int mid = left + (right-left)/2;
if (check(mid, a, k)) {
res = mid;
left = mid + 1;
}else {
right = mid - 1;
}
}
return res;
}
//分为 k 组能否保证每组都大于等于 mid(如果可以说明还可以更大)
public boolean check(int mid, int[] a, int k) {
int sum = 0;
int count = 0;
for (int i = 0; i < a.length; i++) {
sum += a[i];
if (sum >= mid) {
sum = 0;
count++;
}
}
return count >= k;
}
1482. 制作 m 束花所需的最少天数
给你一个整数数组 bloomDay,以及两个整数 m 和 k 。
现需要制作 m 束花。制作花束时,需要使用花园中 相邻的 k 朵花 。
花园中有 n 朵花,第 i 朵花会在 bloomDay[i] 时盛开,恰好 可以用于 一束 花中。 请你返回从花园中摘 m 束花需要等待的最少的天数。如果不能摘到 m 束花则返回 -1 。
示例 1:
输入:bloomDay = [1,10,3,10,2], m = 3, k = 1
输出:3
解释:让我们一起观察这三天的花开过程,x 表示花开,而 _ 表示花还未开。
现在需要制作 3 束花,每束只需要 1 朵。
1 天后:[x, _, _, _, _] // 只能制作 1 束花
2 天后:[x, _, _, _, x] // 只能制作 2 束花
3 天后:[x, _, x, _, x] // 可以制作 3 束花,答案为 3
示例 2:
输入:bloomDay = [1,10,3,10,2], m = 3, k = 2
输出:-1
解释:要制作 3 束花,每束需要 2 朵花,也就是一共需要 6 朵花。而花园中只有 5 朵花,无法满足制作要求,返回 -1 。
示例 3:
输入:bloomDay = [7,7,7,7,12,7,7], m = 2, k = 3
输出:12
解释:要制作 2 束花,每束需要 3 朵。
花园在 7 天后和 12 天后的情况如下:
7 天后:[x, x, x, x, _, x, x]
可以用前 3 朵盛开的花制作第一束花。但不能使用后 3 朵盛开的花,因为它们不相邻。
12 天后:[x, x, x, x, x, x, x]
显然,我们可以用不同的方式制作两束花。
示例 4:
输入:bloomDay = [1000000000,1000000000], m = 1, k = 1
输出:1000000000
解释:需要等 1000000000 天才能采到花来制作花束
示例 5:
输入:bloomDay = [1,10,2,9,3,8,4,7,5,6], m = 4, k = 2
输出:9
提示:
- bloomDay.length == n
- 1 <= n <= 10^5
- 1 <= bloomDay[i] <= 10^9
- 1 <= m <= 10^6
- 1 <= k <= n
解法一
193th 周赛的 T3,没参加,但是在群里听群友讨论了,是个二分,刚刚具体的看了题目,发现其实是很明显的二分答案,很可惜没参加这次比赛,感觉能 A3 道。
public int minDays(int[] bloomDay, int m, int k) {
int n=bloomDay.length;
if(m*k>n) return -1; //花园的花不够
//直接写就完事了,这里数据范围只到 1e9,log(1e9) 很小的,只有 30 左右
int left=1,right=(int)1e9;
int res=right+1;
while(left<=right){
int mid=left+(right-left)/2;
if(check(bloomDay,m,k,mid)){
res=mid;
right=mid-1;
}else{
left=mid+1;
}
}
return res;
}
//check 写的好丑。..
public boolean check(int[] bloomDay,int m,int k,int day){
int i=0;
int count=0;
while(i<bloomDay.length){
int temp=0;
while(i<bloomDay.length){
if(bloomDay[i]<=day){
temp++;
if(temp==k){
count++;
break;
}
i++;
}else{
break;
}
}
if(count>=m) return true;
i++;
}
return false;
}
解法二
看了评论区,然后自己思考了下,改进了check
public int minDays(int[] bloomDay, int m, int k) {
int n=bloomDay.length;
if(m*k>n) return -1; //花园的花不够
//直接写就完事了,这里数据范围只到 1e9,log(1e9) 很小的,只有 30 左右
int left=1,right=(int)1e9;
int res=right+1;
while(left<=right){
int mid=left+(right-left)/2;
if(check(bloomDay,m,k,mid)){
res=mid;
right=mid-1;
}else{
left=mid+1;
}
}
return res;
}
public boolean check(int[] bloomDay,int m,int k,int day){
int i=0;
int count=0;
int temp=0; //相邻的开花数量
for(int d:bloomDay){
if(d<=day){ //花开了 (md,这个 if 写反两次)
temp++;
}else{
temp=0;
}
if(temp==k){
temp=0;
count++;
}
}
return count>=m;
}
378. 有序矩阵中第 K 小的元素
Difficulty: 中等
给定一个 _n x n _矩阵,其中每行和每列元素均按升序排序,找到矩阵中第 k 小的元素。
请注意,它是排序后的第 k 小元素,而不是第 k 个不同的元素。
示例:
matrix = [
[ 1, 5, 9],
[10, 11, 13],
[12, 13, 15]
],
k = 8,
返回 13。
提示:
你可以假设 k 的值永远是有效的,1 ≤ k ≤ n<sup>2 </sup>。
(直接搬运我在 lc 题解区写的 题解)
解法一
小根堆,多路归并,没啥好说的
public int kthSmallest(int[][] matrix, int k) {
PriorityQueue<Pair> pq = new PriorityQueue<>((p1,p2)->matrix[p1.x][p1.y] - matrix[p2.x][p2.y]);
for(int i = 0;i < matrix.length; i++){
pq.add(new Pair(i, 0));
}
while(k > 1){
Pair pair = pq.poll();
if(pair.y + 1 < matrix[0].length){
pq.add(new Pair(pair.x, pair.y+1));
}
k--;
}
return matrix[pq.peek().x][pq.peek().y];
}
class Pair{
int x, y;
public Pair(int x, int y){
this.x = x;
this.y = y;
}
}
解法二
二分答案,我们求的元素一定是在matrix[0][0]~matrix[n-1][n-1]之间,取中间某个元素mid,大于mid的都分布在右下角,小于mid的的分布在右上角,越往右上走,小于mid的元素就越少,大于mid的元素就越多,所以整体是具有单调性的,所以可以二分
然后我认为很关键的一个地方就是二分的写法,我这里用的是 zls 的一个二分模板,两个分支,一个是答案区间,一个是排除区间,在答案区间记录答案,现在问题就是:是用 <= 作为答案区间,还是用 >=做为答案区间?
两种方法的区别就是区间收缩的方式不一样,前者是left=mid+1后者是right=mid-1,所以问题其实就变成了:当**小于等于 mid 的数量==k **的时候,二分的区间应该如何缩减?
其实举个例子就懂了
matrix = [
[ 1, 5, 9],
[10, 11, 13],
[12, 13, 15]
],
k = 2
k=2,对应结果应该是 5,但是我们现在 mid=8,这里 8 和 5 在矩阵中小于等于它们的数量是相同的,这个时候很明显应该缩短 right 去逼近 5,所以我们应该选取>=作为答案区间并记录答案,并且缩短 right 逼近矩阵中真实存在的值
这里是一定是可以取到矩阵中的值的,二分最后会在大于等于区域不断缩减 right 直至不能再缩减,也就是缩减成为矩阵中的元素(再缩减就小于 K 了)
public int kthSmallest(int[][] matrix, int k) {
int n = matrix.length;
int left = matrix[0][0];
int right = matrix[n-1][n-1];
int res = left;
while(left <= right){
int mid = left + (right - left)/2;
//注意这个地方,很关键,核心就是这个等于号的位置,在小于等于 mid 的数量==k 的时候二分的区间应该如何移动
//其实举个例子就懂了,假设 k=2,对于结果应该是 5,但是我们现在 mid=8
//这里 8 和 5 在矩阵中小于等于它们的数量是相同的,这个时候很明显应该缩短 right 去逼近 5
//所以我们应该在二分的大于等于区间记录答案,并且缩短 right
if (check(matrix, mid) >= k){
res = mid;
right = mid - 1;
}else{
left = mid + 1;
}
}
return res;
}
//检查数组中小于等于 mid 的个数
public int check(int[][] matrix, int mid){
int row = matrix.length-1, column = 0;
int count = 0;
int lastRow = 0;
while(row >= 0){
while (column < matrix[0].length && matrix[row][column] <= mid){
column++;
lastRow++;
}
count += lastRow;
row--;
}
return count;
}
441. 排列硬币
Difficulty: 简单
你总共有 _n _枚硬币,你需要将它们摆成一个阶梯形状,第 _k _行就必须正好有 _k _枚硬币。
给定一个数字 n,找出可形成完整阶梯行的总行数。
_n _是一个非负整数,并且在 32 位有符号整型的范围内。
示例 1:
n = 5
硬币可排列成以下几行:
¤
¤ ¤
因为第三行不完整,所以返回 2.
示例 2:
n = 8
硬币可排列成以下几行:
¤
¤ ¤
¤ ¤ ¤
¤ ¤
因为第四行不完整,所以返回 3.
解法一
因为是从二分的 tag 来的,所以知道是二分,然后看了题,确定了有二分答案性质,然后直接二分,可是没想到居然溢出了,看来还是有点大意了啊,时间复杂度 O(logN)
//二分答案
public int arrangeCoins(int n) {
int left = 1;
int right = n;
int res = 0;
while(left <= right){
long mid = left + (right - left)/2;
long sum = (1 + mid) * mid / 2;
if(sum <= n){
res = (int)mid;
left = (int)mid + 1;
}else{
right = (int)mid - 1;
}
}
return res;
}
这题当然也可以直接模拟,不过意义不大,这题还有数学的解法,根据求和公式直接算出根,然后利用 sqrt 函数,这样并不会比二分快多少,sqrt 也是 logN 级别的,而且面试官应该也不希望你利用库函数(当然人如果能手写牛顿迭代法那肯定没问题)
174. 地下城游戏
Difficulty: 困难
一些恶魔抓住了公主(P)并将她关在了地下城的右下角。地下城是由 M x N 个房间组成的二维网格。我们英勇的骑士(K)最初被安置在左上角的房间里,他必须穿过地下城并通过对抗恶魔来拯救公主。
骑士的初始健康点数为一个正整数。如果他的健康点数在某一时刻降至 0 或以下,他会立即死亡。
有些房间由恶魔守卫,因此骑士在进入这些房间时会失去健康点数(若房间里的值为负整数,则表示骑士将损失健康点数);其他房间要么是空的(房间里的值为 0),要么包含增加骑士健康点数的魔法球(若房间里的值为正整数,则表示骑士将增加健康点数)。
为了尽快到达公主,骑士决定每次只向右或向下移动一步。
编写一个函数来计算确保骑士能够拯救到公主所需的最低初始健康点数。
例如,考虑到如下布局的地下城,如果骑士遵循最佳路径 右 -> 右 -> 下 -> 下,则骑士的初始健康点数至少为 7。
| -2 (K) | -3 | 3 |
| -5 | -10 | 1 |
| 10 | 30 | -5 (P) |
说明:
-
骑士的健康点数没有上限。
-
任何房间都可能对骑士的健康点数造成威胁,也可能增加骑士的健康点数,包括骑士进入的左上角房间以及公主被监禁的右下角房间。
解法一
以后每日一题没写出来之前绝壁不看群了,看了一眼群,看见群友讨论了这题,说了二分和 dp,然后我就直接向二分的方向去想了,如果独立的想的话,应该也是可以得出二分的解法的,毕竟题目的描述很明显就是二分答案,最低的健康血量,大于这个血量的肯定可以救出来,小于这个血量的肯定救不出来,所以 check 就是判断在某个血量下,能否拯救到公主(DP)
时间复杂度 O(N^2logN)(其实我认为也可以当作 N^2 毕竟上下界都确定了,logN 也就 30 左右),这种解法也挺不错的,融合了二分和 dp
public int calculateMinimumHP(int[][] dungeon) {
int left = 0;
int right = Integer.MAX_VALUE;
int res = 0;
while(left <= right){
int mid = left + (right-left)/2;
if(check(dungeon, mid)){
res = mid;
right = mid - 1;
}else{
left = mid + 1;
}
}
return res;
}
public boolean check(int[][] dungeon, int live){
int m = dungeon.length;
int n = dungeon[0].length;
int INF = Integer.MIN_VALUE;
//live 的血量从左上到 dungeon[i][j] 的剩余最多血量
int[][] dp = new int[m+1][n+1];
//地牢外围加上 INF 的围墙,简化逻辑
Arrays.fill(dp[0], INF);
dp[0][1] = live;
for(int i = 1; i <= m; i++){
dp[i][0] = INF;
for(int j = 1; j <= n; j++){
if(dp[i-1][j] <= 0 && dp[i][j-1] <=0 ){
dp[i][j] = INF; //无法到达这里
}else{
dp[i][j] = dungeon[i-1][j-1] + Math.max(dp[i][j-1], dp[i-1][j]);
}
}
}
return dp[m][n] > 0;
}
当然这题也有纯 dp 的做法,很可惜,我压根没往上面想,我只想着二分 dp,写完了 AC 之后就去看评论区了,结果发现大家都是直接 dp 的。然后还看到了一个关键词:逆向 dp,然后赶紧关了评论区回来写了下面的 dp 解法
解法二
/*
-2 -3 3
-5 -10 1
10 30 -5 1
7 5 2
6 11 5
1 1 6
*/
public int calculateMinimumHP(int[][] dungeon) {
int m = dungeon.length;
int n = dungeon[0].length;
int INF = Integer.MAX_VALUE;
//从 dungeon[i-1][j-1] 到右下角至少要多少血量
int[][] dp = new int[m+1][n+1];
Arrays.fill(dp[m], INF);//末行
dp[m][n-1] = 1; //初始血量
for (int i = m-1; i >= 0; i--) {
dp[i][n] = INF; //首列和尾列
for (int j = n-1; j >= 0; j--) {
dp[i][j] = Math.max(Math.min(dp[i+1][j], dp[i][j+1]) - dungeon[i][j], 1);
}
}
return dp[0][0];
}
这题为啥不能正向 dp 呢,设dp[i][j]为从左上角到 i,j 所需要的最低血量?其实这个很明显就是有问题的,没办法转移,dp[i][j]和dp[i-1][j]没有任何关系,都不一定是同一条路径
848. 加油站之间的最小距离(LintCode)
在水平数轴上,我们有加油站:stations[0], stations[1], …, stations[N-1], 这里 N = stations.length。
现在,我们再增加 K 个加油站,D 表示相邻加油站之间的最大距离,这样 D 就变小了。
返回所有可能值 D 中最小值。
- stations.length 为整数,范围 [10, 2000].
- stations[i] 为整数,范围 [0, 10^8].
- K 为整数,范围 [1, 10^6].
- 答案范围在 10 ^ -6 之内的有理数。
样例 1:
输入:stations = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10],K = 9
输出:0.50
解释:相邻加油站的距离均为 0.50
样例 2:
输入:stations = [3,6,12,19,33,44,67,72,89,95],K = 2
输出:14.00
解释:在距离 86 处建造加油站 (fix: 还有 58 处)
解法一
二分答案的性质很明显,但是这里和之前的不一样,这里是浮点数二分,和整数的不太一样,浮点数/2 的时候都是实际的一分为 2,不会有整除的问题,同时题目给出了 eps=1e-6,只要 left 和 right 误差在这个范围内就是合法的,并不是要求 left 和 right 相等,这里还有一个问题,就是这里如果 eps 太小的话由于精度问题还是可能会 tle,这个时候就可以采取固定循环次数的方式逼近,一般取 100,200 就够了
public double minmaxGasDist(int[] stations, int k) {
// Write your code here
double left = 0;
double right = 1e8+1;
double res = right;
//for (int i = 0; i <= 100; i++){
while (right-left >= 1e-6){
double mid = left+(right-left)/2;
if (check(stations, k, mid)) {
res = mid;
right = mid;
}else{
left = mid;
}
}
return res;
}
public boolean check(int[] stations, int k, double D) {
int count = 0;
for (int i = 1; i < stations.length; i++) {
count += (stations[i]-stations[i-1]) / D;
}
return count <= k;
}
5489. 两球之间的磁力
Difficulty: 中等
在代号为 C-137 的地球上,Rick 发现如果他将两个球放在他新发明的篮子里,它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子,第 i 个篮子的位置在 position[i] ,Morty 想把 m 个球放到这些篮子里,使得任意两球间 最小磁力 最大。
已知两个球如果分别位于 x 和 y ,那么它们之间的磁力为 |x - y| 。
给你一个整数数组 position 和一个整数 m ,请你返回最大化的最小磁力。
示例 1:

输入:position = [1,2,3,4,7], m = 3
输出:3
解释:将 3 个球分别放入位于 1,4 和 7 的三个篮子,两球间的磁力分别为 [3, 3, 6]。最小磁力为 3 。我们没办法让最小磁力大于 3 。
示例 2:
输入:position = [5,4,3,2,1,1000000000], m = 2
输出:999999999
解释:我们使用位于 1 和 1000000000 的篮子时最小磁力最大。
提示:
n == position.length2 <= n <= 10^51 <= position[i] <= 10^9- 所有
position中的整数 互不相同 。 2 <= m <= position.length
解法一
202 周赛 T3,没参赛(实在是没时间打)赛后独立的写出来了,很明显是二分答案,不过这里有一点小不同
public int maxDistance(int[] position, int m) {
Arrays.sort(position);
int left = 1;
int right = (int)1e9+1;
int res = 1;
while (left <= right) {
int mid = left + (right-left)/2;
if (check(position, m, mid)) {
res = mid;
left = mid + 1;
}else{
right = mid - 1;
}
}
return res;
}
//1 1000 2000 3000 m=3
//验证在距离至少为 force 的情况下能否放下所有的球,然后增大 force 逼近答案
//所以 check 验证成功的不一定是合法的答案,但是最终一定会到达 real ans
//类似【378. 有序矩阵中第 K 小的元素】这道题
public boolean check(int[] position, int m, int force) {
int last = position[0];
m--;
for (int i = 1; i < position.length; i++) {
if (position[i]-last < force) {
continue;
}
last = position[i];
m--;
if (m==0) return true;
}
return false;
}
check 类似 [378. 有序矩阵中第 K 小的元素](#378-有序矩阵中第 k 小的元素)这道题,都是逼近答案,而不是验证答案,其实一开始我的 check 不是这样写的,写的很丑,这里看了别人的写法发现 continue 有时候还是挺好用的