LeetCode363. 矩形区域不超过 K 的最大数值和
363. 矩形区域不超过 K 的最大数值和
Difficulty: 困难
给你一个 m x n 的矩阵 matrix 和一个整数 k ,找出并返回矩阵内部矩形区域的不超过 k 的最大数值和。
题目数据保证总会存在一个数值和不超过 k 的矩形区域。
示例 1:
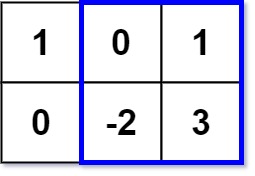
输入:matrix = [[1,0,1],[0,-2,3]], k = 2
输出:2
解释:蓝色边框圈出来的矩形区域 [[0, 1], [-2, 3]] 的数值和是 2,且 2 是不超过 k 的最大数字(k = 2)。
示例 2:
输入:matrix = [[2,2,-1]], k = 3
输出:3
提示:
- $m = \text{matrix.length}$
- $n = \text{matrix[i].length}$
- $1 \leq m, n \leq 100$
- $-100 \leq \text{matrix[i][j]} \leq 100$
- $-10^5 \leq k \leq 10^5$
进阶:如果行数远大于列数,该如何设计解决方案?
解法一
这个题给了我很大的启发,对枚举方法又多了点认识,这题常规暴力的做法是直接枚举所有的矩形,然后判断,结合二维前缀和,时间复杂度 $O(m^2n^2)$ ,已经在 T 的边缘了,所以我们要优化一下算法。
这里其实就涉及到一个优化枚举的一般思路,前面做过的 最大子序和 就可以用类似的枚举优化的思路(这题有更简单的 dp 做法),常规的暴力枚举可以借助前缀和枚举所有的子区间的和,求一个最大值,但是这样时间复杂度将会是 $O(n^2)$ ,那么我们就可以考虑优化枚举方法,我们最终的目标是求最大的 $s_j-s_i$ ,所以我们可以考虑将 $j$ 固定,然后借助一些数据结构,比如小根堆,搜索树(其实一个变量就行了。..)直接求出 $j$ 固定时,前面最小的 $s_i$ ,如此只需要遍历一遍就能得到最大的子序和。
回到这个题,上面最大子序和是一维的,这里是二维的,我们可以将其抽象为一维的,我们枚举所有矩形其实就是在枚举矩形的四条边 $l,r,u,d$ ,但是时间复杂度过高,那么我们可以采用前面的优化思路,将三条边 $r,u,d$ 固定

我们要求的矩形面积是 $s[r]-s[l]$ ,结合这题的要求就是 $s[r]-s[l] \leq k$ ,所以我们要求的就是 $r$ 前面满足 $s[l] \geq s[r]-k$ 的最小 $s[l]$ ,显然只要我们将前面的所有元素 $s[i]$ 有序的存储下来,就可以使用二分来查找,这里我们就不必再造轮子了,直接借助TreeSet,底层结构是红黑树,查询复杂度 $O(\log{n})$ ,整体复杂度 $O(m^2n\log{n})$ 。进阶的做法多判断一下就行了,对复杂度没有本质的影响,不多写了。
代码实现如下:
import java.util.*;
class Solution {
public int maxSumSubmatrix(int[][] matrix, int k) {
int m = matrix.length, n = matrix[0].length;
int[][] s = new int[m+1][n+1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
s[i][j] = matrix[i-1][j-1] + s[i-1][j] + s[i][j-1] -s[i-1][j-1];
}
}
TreeSet<Integer> set = new TreeSet<>();
int res = -0x3f3f3f3f;
for (int u = 1; u <= m; u++) {
for (int d = u; d <= m; d++) {
set.clear();
set.add(0);
//0 lv rv, rv-lv <= k lv >= rv-k
for (int r = 1; r <= n; r++) {
int rv = s[d][r] - s[u-1][r];
Integer lv = set.ceiling(rv-k);
set.add(rv);
if (lv == null) continue;
res = Math.max(res, rv-lv);
}
}
}
return res;
}
}