Lc1621. 大小为 K 的不重叠线段的数目
1621. 大小为 K 的不重叠线段的数目
Difficulty: 中等
给你一维空间的 n 个点,其中第 i 个点(编号从 0 到 n-1)位于 x = i 处,请你找到 恰好 k 个不重叠 线段且每个线段至少覆盖两个点的方案数。线段的两个端点必须都是 整数坐标 。这 k 个线段不需要全部覆盖全部 n 个点,且它们的端点可以重合。
请你返回 k 个不重叠线段的方案数。由于答案可能很大,请将结果对 1e9+7 取余 后返回。
示例 1:
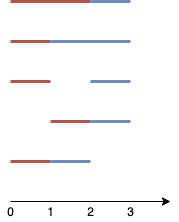
输入:n = 4, k = 2
输出:5
解释:
如图所示,两个线段分别用红色和蓝色标出。
上图展示了 5 种不同的方案 {(0,2),(2,3)},{(0,1),(1,3)},{(0,1),(2,3)},{(1,2),(2,3)},{(0,1),(1,2)} 。
示例 2:
输入:n = 3, k = 1
输出:3
解释:总共有 3 种不同的方案 {(0,1)}, {(0,2)}, {(1,2)} 。
示例 3:
输入:n = 30, k = 7
输出:796297179
解释:画 7 条线段的总方案数为 3796297200 种。将这个数对 109 + 7 取余得到 796297179 。
示例 4:
输入:n = 5, k = 3
输出:7
示例 5:
输入:n = 3, k = 2
输出:1
提示:
2 <= n <= 10001 <= k <= n-1
解法一
这题题想了好久,最终还是妥协了,看了题解,发现有暴搜+记忆化的解法,试了下,T 了
int MOD = (int)1e9+7;
//写个暴搜试试(T 了)
public int numberOfSets2(int n, int k) {
Long[][] dp = new Long[n+1][k+1];
return dfs(n, k, dp);
}
//n 个点放 k 条线段的方案数
public int dfs(int n, int k, Long[][] dp) {
if (dp[n][k] != null) {
return dp[n][k].intValue();
}
if (k == 0) {
return 1;
}
if (k == 1) {
return (n-1)*n/2;
}
long res = 0;
for (int i = 1; n-i >= k-2; i++) {
//前 (i+1) 个点放一条线段有 i 种方案(刨开之前的方案)
res += 1l * i * dfs(n-i, k-1, dp);
res = (res + MOD) % MOD;
}
dp[n][k] = res;
return (int)res;
}
解法二
其实这里就两个状态,点数 $n$ 和线段条数 $k$ ,所以设计状态的时候肯定是和这两个有关。乍一看这里任意相邻两个点数之间是没有任何关联的,所以我们需要建立联系。这个联系其实就是线段有没有覆盖到 $n$
我们设 $dp[i][j]$ 代表长度为 $i$ 的节点放置 $j$ 条线段有几种方案,状态的转移分两种情况
- 最后一条线段不覆盖右端点,那么递推就直接 $dp[i][j] = dp[i-1][j]$
- 最后一条线段覆盖右端点,枚举最后一条线段的长度所对应的 $dp[i-len][j-1]$ 累加起来
代码实现如下:
public int numberOfSets(int n, int k) {
int MOD = (int)1e9+7;
long[][] dp = new long[n+1][k+1];
for (int i = 0; i <= n; i++) {
dp[i][0] = 1;
}
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= Math.min(i-1, k); j++) {
//j 没有覆盖右端点的情况
dp[i][j] = dp[i-1][j];
//枚举 j 覆盖区间右端点的所有情况,注意从 1 开始
for (int s = 1; s < i; s++) {
dp[i][j] = (dp[i][j] + dp[s][j-1]) % MOD;
}
}
}
return (int) dp[n][k];
}
这里数据范围是 $1e3$ ,显然 $O(n^3)$ 是过不了的,所以需要优化。这里发现第三重循环中求的其实是前缀和,所以可以通过前缀和优化成 $O(n^2)$
public int numberOfSets(int n, int k) {
int MOD = (int)1e9+7;
long[][] dp = new long[n+1][k+1];
long[][] sum = new long[n+1][k+1];
for (int i = 1; i <= n; i++) {
dp[i][0] = 1;
sum[i][0] = sum[i-1][0] + 1;
}
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= Math.min(i-1, k); j++) {
//j 没有覆盖右端点的情况
dp[i][j] = dp[i-1][j];
//枚举 j 覆盖区间右端点的所有情况,注意从 1 开始
// for (int s = 1; s < i; s++) {
// dp[i][j] = (dp[i][j] + dp[s][j-1]) % MOD;
// }
dp[i][j] = (dp[i][j] + sum[i-1][j-1]) % MOD;
sum[i][j] = sum[i-1][j] + dp[i][j];
}
}
return (int) dp[n][k];
}
解法三
这种 DP 的方式更好理解
$dp[i][j][0]$ : 前 $i$ 个点放 $j$ 条线段,第 $j$ 条线段没有覆盖右端点,所以显然 $dp[i][j][0] = dp[i-1][j][0] + dp[i-1][j][1]$
$dp[i][j][1]$ : 前 $i$ 个点放 $j$ 条线段,第 $j$ 条线段覆盖右端点(可以延长),首先 j 位置单独成一条线段 $dp[i-1][j-1][0] + dp[i-1][j-1][1]$ ,然后就是 $j$ 位置和前面的连成一条线段的 $dp[i-1][j]$
public int numberOfSets(int n, int k) {
int MOD = (int)1e9+7;
//dp[i][j][0]: 前 i 个点放 j 条线段,第 j 条线段没有覆盖右端点
//dp[i][j][1]: 前 i 个点放 j 条线段,第 j 条线段覆盖右端点(可以延长)
long[][][] dp = new long[n+1][k+1][2];
for (int i = 0; i <= n; i++) {
dp[i][0][0] = 1;
}
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= Math.min(i-1, k); j++) {
dp[i][j][0] = dp[i-1][j][0] + dp[i-1][j][1];
dp[i][j][1] = dp[i-1][j-1][0] + dp[i-1][j-1][1] + dp[i-1][j][1];
dp[i][j][0] = (dp[i][j][0] + MOD) % MOD;
dp[i][j][1] = (dp[i][j][1] + MOD) % MOD;
}
}
return (int)(dp[n][k][0] + dp[n][k][1] + MOD) % MOD;
}
解法四
其实是上面解法的优化递推,省去了前缀和的空间,直接从状态转移方程上进行优化
 列出递推中的连续两项,然后进行合并优化,直接得到递推公式
列出递推中的连续两项,然后进行合并优化,直接得到递推公式
//有一点技巧性的递推
public int numberOfSets(int n, int k) {
int MOD = (int)1e9+7;
//n 个点,放 k 个线段,不重叠的方案数
long[][] dp = new long[n+1][k+1];
for (int i = 0; i <= n; i++) {
dp[i][0] = 1;
}
for (int i = 2; i <= n; i++) {
for (int j = 1; j <= i-1 && j <= k; j++) {
//dp[2][1] = 2*dp[1][1] - dp[0][1] + dp[1][0]
dp[i][j] = 2*dp[i-1][j] - dp[i-2][j] + dp[i-1][j-1];
dp[i][j] = (dp[i][j] + MOD) % MOD;
}
}
return (int)dp[n][k];
}
解法五
数学法,看不懂,求 C(n+k-1, 2k)