基础:前缀和&差分
工作后好久没发新文章了,有些文章其实是很久之前就写完了,但是一直没发。最近搬家了,开始了新的生活,先慢慢找回之前的节奏,把坑都填完
796. 子矩阵的和(模板题)
输入一个 $n$ 行 $m$ 列的整数矩阵,再输入 $q$ 个询问,每个询问包含四个整数 $x_1,y_1,x_2,y_2$ ,表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。
输入格式
第一行包含三个整数 $n,m,q$ 。
接下来 $n$ 行,每行包含 $m$ 个整数,表示整数矩阵。
接下来 $q$ 行,每行包含四个整数 $x_1,y_1,x_2,y_2$ ,表示一组询问。
输出格式
共 $q$ 行,每行输出一个询问的结果。
数据范围
- $1≤n,m≤1000$
- $1≤q≤200000$
- $1≤x1≤x_2≤n$
- $1≤y1≤y_2≤m$
- $−1000≤v≤1000$
输入样例:
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4
输出样例:
17
27
21
解法一
二维前缀和模板,一维的模板比较简单就不多写了
import java.util.*;
import java.io.*;
class Main {
public static void main(String... args) throws Exception {
PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// BufferedReader br = new BufferedReader(new InputStreamReader(new FileInputStream("./input.txt")));
int[] in = read(br);
int N = in[0], M = in[1], Q = in[2];
int[][] sum = new int[N+1][M+1];
for (int i = 1; i <= N; i++) {
int[] t = read(br);
for (int j = 1; j <= M; j++) {
sum[i][j] = t[j-1] + sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1];
}
}
for (int i = 0; i < Q; i++) {
int[] q = read(br);
int x1 = q[0], y1 = q[1];
int x2 = q[2], y2 = q[3];
out.println(sum[x2][y2]-(sum[x1-1][y2]+sum[x2][y1-1])+sum[x1-1][y1-1]);
}
out.flush();
}
public static int[] read(BufferedReader br) throws Exception {
return Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
}
}
99. 激光炸弹
地图上有 $N$ 个目标,用整数 $X_i,Y_i$ 表示目标在地图上的位置,每个目标都有一个价值 $W_i$ 。
注意:不同目标可能在同一位置。
现在有一种新型的激光炸弹,可以摧毁一个包含 $R×R$ 个位置的正方形内的所有目标。
激光炸弹的投放是通过卫星定位的,但其有一个缺点,就是其爆炸范围,即那个正方形的边必须和 $x,y$ 轴平行。
求一颗炸弹最多能炸掉地图上总价值为多少的目标。
输入格式
第一行输入正整数 $N$ 和 $R$ ,分别代表地图上的目标数目和正方形的边长,数据用空格隔开。
接下来 $N$ 行,每行输入一组数据,每组数据包括三个整数 $X_i,Y_i,W_i$ ,分别代表目标的 $x$ 坐标, $y$ 坐标和价值,数据用空格隔开。
输出格式
输出一个正整数,代表一颗炸弹最多能炸掉地图上目标的总价值数目。
数据范围
- $0≤R≤10^9$
- $0<N≤10000$
- $0≤X_i,Y_i≤5000$
- $0≤W_i≤1000$
输入样例:
2 1
0 0 1
1 1 1
输出样例:
1
解法一
其实也是个模板题。.. 注意多个目标会在同一个点
import java.util.*;
import java.io.*;
class Main {
public static void main(String... args) throws Exception {
PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// BufferedReader br = new BufferedReader(new InputStreamReader(new FileInputStream("./input.txt")));
int[] in = read(br);
int MAX = 5010;
int N = in[0], R = in[1];
int[][] w = new int[MAX][MAX];
for (int i = 0; i < N; i++) {
int[] t = read(br);
w[t[0]][t[1]] += t[2];
}
int[][] sum = new int[MAX][MAX];
for (int i = 1; i < MAX; i++) {
for (int j = 1; j < MAX; j++) {
sum[i][j] = w[i-1][j-1] + sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1];
}
}
int res = 0;
for (int i = 1; i < MAX; i++) {
if (i+R-1 >= MAX) break;
for (int j = 1; j < MAX; j++) {
if (j+R-1 >= MAX) break;
int i2 = i+R-1, j2 = j+R-1;
res = Math.max(res, sum[i2][j2]-sum[i-1][j2]-sum[i2][j-1]+sum[i-1][j-1]);
}
}
out.println(res);
out.flush();
}
public static int[] read(BufferedReader br) throws Exception {
return Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
}
}
1292. 元素和小于等于阈值的正方形的最大边长
给你一个大小为 m x n 的矩阵 mat 和一个整数阈值 threshold。
请你返回元素总和小于或等于阈值的正方形区域的最大边长;如果没有这样的正方形区域,则返回 $0$ 。
示例 1:
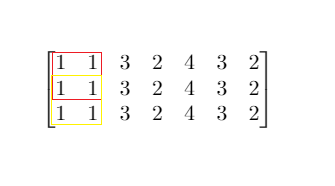
输入:mat = [[1,1,3,2,4,3,2],[1,1,3,2,4,3,2],[1,1,3,2,4,3,2]], threshold = 4
输出:2
解释:总和小于 4 的正方形的最大边长为 2,如图所示。
示例 2:
输入:mat = [[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2],[2,2,2,2,2]], threshold = 1
输出:0
示例 3:
输入:mat = [[1,1,1,1],[1,0,0,0],[1,0,0,0],[1,0,0,0]], threshold = 6
输出:3
示例 4:
输入:mat = [[18,70],[61,1],[25,85],[14,40],[11,96],[97,96],[63,45]], threshold = 40184
输出:2
提示:
- $1 \leq m, n \leq 300$
- $m = mat.length$
- $n = mat[i].length$
- $0 \leq mat[i][j] \leq 10000$
- $0 \leq threshold \leq 10^5$
解法一
这里直接将之前的 题解 搬过来了,相对来说这题就没那么模板了,结合了二分,还是挺好的
首先看到这道题就意识到了这是个二分答案的题,直接二分边长就行了,左端点 $1$ ,右端点 $\min(m,n)$ ,某个边长 $x$ 满足的时候,大于 $x$ 的都满足,某个 $x$ 不满足的时候,小于 $x$ 的都不满足,解空间具有单调性
所以关键问题就是check怎么写,如果直接暴力枚举所有矩形然后计算时间复杂度会很恐怖,这个时候就可以引入二维前缀和,在 $O(1)$ 的时间下求出子矩阵的和
class Solution {
int[][] sum;
public int maxSideLength(int[][] mat, int threshold) {
int m = mat.length;
int n = mat[0].length;
int left = 1, right = Math.min(m, n);
sum = new int[m+1][n+1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
sum[i][j] = mat[i-1][j-1] + sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1];
}
}
int res = 0;
while(left <= right){
int mid = left + (right-left)/2;
if(check(mat, mid, threshold)){
res = mid;
left = mid+1;
}else{
right = mid-1;
}
}
return res;
}
public boolean check(int[][] mat, int side, int threshold){
//枚举所有的左端点
for (int i = 1; i+side-1 <= mat.length; i++) {
for (int j = 1; j+side-1 <= mat[0].length; j++) {
int ri = i+side-1, rj = j+side-1;
if(sum[ri][rj]-sum[i-1][rj]-sum[ri][j-1]+sum[i-1][j-1] <= threshold){
return true;
}
}
}
return false;
}
}
798. 差分矩阵(模板题)
输入一个 $n$ 行 $m$ 列的整数矩阵,再输入 $q$ 个操作,每个操作包含五个整数 $x_1,y_1,x_2,y_2,c$ ,其中 $(x_1,y_1)$ 和 $(x_2,y_2)$ 表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上 $c$ 。
请你将进行完所有操作后的矩阵输出。
输入格式
第一行包含整数 $n,m,q$ 。
接下来 $n$ 行,每行包含 $m$ 个整数,表示整数矩阵。
接下来 $q$ 行,每行包含 $5$ 个整数 $x_1,y_1,x_2,y_2,c$ ,表示一个操作。
输出格式
共 $n$ 行,每行 $m$ 个整数,表示所有操作进行完毕后的最终矩阵。
数据范围
- $1≤n,m≤1000$
- $1≤q≤100000$
- $1≤x1≤x2≤n$
- $1≤y1≤y2≤m$
- $−1000≤c≤1000$
- $−1000≤v≤1000$
输入样例:
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1
输出样例:
2 3 4 1
4 3 4 1
2 2 2 2
解法一
二维差分模板题,一维的模板也比较简单就不多写了,二维的需要多说几句
和前缀和相反,矩阵中某个元素 $matrix[i][j]$ 的值是差分数组 $(0,0)$ 到 $(i,j)$ 的二维前缀和,所以当我们给某个点 $(i,j)$ 的差分值加 $c$ 的时候,会使以该点为左上角,到整个矩阵的右下角 $(n,m)$ 的矩阵区域元素值增加 $c$
,如下图当给 $(x_1, y_1)$ 的差分值增加 $c$ 的时候,会使得整个蓝色框区域的矩阵元素值都增加 $c$
 但是这里我们只希望子矩阵 $(x_1,y_1),(x_2,y_2)$ 的值增加,所以我们需要将其它区域的值减回去。所以我们给 $(x_1,y_2+1)$ 以及 $(x_2+1,y_1)$ 的差分值减 $c$ ,注意这两块有一个重合区域 $(x_2+1,y_2+1)$ 多减了一次,我们将其加回来就行了
但是这里我们只希望子矩阵 $(x_1,y_1),(x_2,y_2)$ 的值增加,所以我们需要将其它区域的值减回去。所以我们给 $(x_1,y_2+1)$ 以及 $(x_2+1,y_1)$ 的差分值减 $c$ ,注意这两块有一个重合区域 $(x_2+1,y_2+1)$ 多减了一次,我们将其加回来就行了
import java.util.*;
import java.io.*;
class Main {
static int[][] diff;
static int n, m, q;
public static void main(String... args) throws Exception {
PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// BufferedReader br = new BufferedReader(new InputStreamReader(new FileInputStream("./input.txt")));
int[] in = read(br);
n = in[0]; m = in[1]; q = in[2];
diff = new int[n+2][m+2];
for (int i = 1; i <= n; i++) {
int[] t = read(br);
for (int j = 1; j <= m; j++) {
incr(i, j, i, j, t[j-1]);
}
}
for (int i = 0; i < q; i++) {
int[] q = read(br);
incr(q[0], q[1], q[2], q[3], q[4]);
}
int[][] matrix = new int[n+2][m+2];
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) {
matrix[i][j] = diff[i][j] + matrix[i-1][j] + matrix[i][j-1] - matrix[i-1][j-1];
out.print(matrix[i][j] + " ");
}
out.println();
}
out.flush();
}
public static void incr(int x1, int y1, int x2, int y2, int c) {
diff[x1][y1] += c;
diff[x1][y2+1] -= c;
diff[x2+1][y1] -= c;
diff[x2+1][y2+1] += c;
}
public static int[] read(BufferedReader br) throws Exception {
return Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
}
}
100. 增减序列
给定一个长度为 $n$ 的数列 $a_1,a_2,…,a_n$ ,每次可以选择一个区间 $[l,r]$ ,使下标在这个区间内的数都加一或者都减一。
求至少需要多少次操作才能使数列中的所有数都一样,并求出在保证最少次数的前提下,最终得到的数列可能有多少种。
输入格式
第一行输入正整数 $n$ 。
接下来 $n$ 行,每行输入一个整数,第 $i+1$ 行的整数代表 $a_i$ 。
输出格式
第一行输出最少操作次数。
第二行输出最终能得到多少种结果。
数据范围
- $0<n≤105$
- $0≤a_i<2147483648$
输入样例:
4
1
2
输出样例:
1
2
解法一
构建差分数组 $d$ ,根据题目要求,我们的目标就是使得 $d_{i(2 \leq i \leq n)}=0$ 的最小操作次数,一次操作可以使得 $d$ 中任意两个元素,一个加 1,一个减 1,并且求保证最小操作次数的同时, $d_1$ 有几种取值情况
这里我们可以将操作按照两个元素的位置进行分类:
- 当 $2 \leq i \leq j \leq n$ 时, $d_i$ 加一(减一), $d_j$ 减一(加一)
- 当 $i=1 \And 2 \leq j \leq n$ 时, $d_1$ 加一(减一), $d_j$ 减一(加一),这种情况就只会修改 $d_{j(2 \leq j \leq n)}$ 中的一个值,同时使得 $d_1$ 值不同
- 当 $2 \leq i \leq n \And j=n$ 时, $d_i$ 加一(减一), $d_n$ 减一(加一)
- 当 $i=1 \And j=n$ 时,整体加减一,没有意义
设 $d_{i(2 \leq i \leq n)}$ 中正数之和为 $p$ ,负数绝对值之和为 $q$ ,那么最快使得 $d_{i(2 \leq i \leq n)}=0$ 的操作方式就是每次从中选取一个正数一个负数,使得正数减一,负数加一,操作次数为 $\min(p,q)$ ,这样正负数配对后,剩下的部分就选择操作 2 或者操作 3 进行加一或者减一使其归 0,操作次数为 $|p-q|$ ,所以操作总数为: $\min(p,q)+|p-q| = \max(p,q)$
第二问求 $d_1$ 的取值情况,其实就是在执行完操作 1 后,剩下的部分执行 2 和 3 所能得到的不同的 $d_1$ 值,而这 2 种操作中能影响 $d_1$ 的值的就只有第 2 类操作,执行 $x$ 次第二类操作,就会使得 $d_1$ 加 $x$ 或者减 $x$ ( $p$ 较大时 $d_1$ 加 $x$ ,反之减 $x$ ),执行不同的次数,就能得到不同的 $d_1$ 值,执行完操作 1 后剩余的部分一共 $|p-q|$ ,所以操作 2 的执行次数就有 $|p-q|+1$ 种情况,对应 $|p-q|+1$ 种 $d_1$ 值
import java.util.*;
import java.io.*;
class Main {
public static void main(String... args) throws Exception {
PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// BufferedReader br = new BufferedReader(new InputStreamReader(new FileInputStream("./input.txt")));
int N = read(br);
int[] diff = new int[N+2];
for (int i = 1; i <= N; i++) {
int t = read(br);
diff[i] += t; diff[i+1] -= t;
}
long p = 0, q = 0;
for (int i = 2; i <= N; i++) {
if (diff[i] > 0) {
p += diff[i];
} else {
q -= diff[i];
}
}
out.println(Math.max(p, q));
out.println(Math.abs(p-q)+1);
out.flush();
}
public static int read(BufferedReader br) throws Exception {
return Integer.valueOf(br.readLine());
}
}
1526. 形成目标数组的子数组最少增加次数
Difficulty: 困难
给你一个整数数组 target 和一个数组 initial ,initial 数组与 target 数组有同样的维度,且一开始全部为 0 。
请你返回从 initial 得到 target 的最少操作次数,每次操作需遵循以下规则:
- 在
initial中选择 任意 子数组,并将子数组中每个元素增加 1 。
答案保证在 32 位有符号整数以内。
示例 1:
输入:target = [1,2,3,2,1]
输出:3
解释:我们需要至少 3 次操作从 intial 数组得到 target 数组。
[0,0,0,0,0] 将下标为 0 到 4 的元素(包含二者)加 1 。
[1,1,1,1,1] 将下标为 1 到 3 的元素(包含二者)加 1 。
[1,2,2,2,1] 将下表为 2 的元素增加 1 。
[1,2,3,2,1] 得到了目标数组。
示例 2:
输入:target = [3,1,1,2]
输出:4
解释:(initial)[0,0,0,0] -> [1,1,1,1] -> [1,1,1,2] -> [2,1,1,2] -> [3,1,1,2] (target) 。
示例 3:
输入:target = [3,1,5,4,2]
输出:7
解释:(initial)[0,0,0,0,0] -> [1,1,1,1,1] -> [2,1,1,1,1] -> [3,1,1,1,1]
-> [3,1,2,2,2] -> [3,1,3,3,2] -> [3,1,4,4,2] -> [3,1,5,4,2] (target)。
示例 4:
输入:target = [1,1,1,1]
输出:1
提示:
- $1 \leq target.length \leq 10^5$
- $1 \leq target[i] \leq 10^5$
解法一
31th 双周赛 t4,首先明白一点,将数组从 $[0…0]$ 通过加一变为target等价于将target通过减一变为 $[0…0]$
和上面一题一样,不过这题是要连同 $d_1$ 一起变为 0,且 $a_i\geq 1$ ,所以 $\sum_{i=0}^nd_i \geq 1$ ,对应上题中就是 $p > q$ ,所以最小操作次数就是 $p$
class Solution:
def minNumberOperations(self, target: List[int]) -> int:
res = target[0]
for i in range(1, len(target)):
if (d := target[i]-target[i-1]) > 0:
res += d
return res